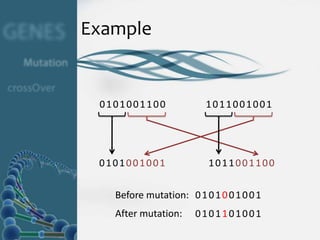
The document provides an overview of genetic algorithms. It describes how genetic algorithms are inspired by natural selection and survival of the fittest. A genetic algorithm uses a population of solutions that evolves toward better solutions, where the fittest solutions are more likely to reproduce and pass on their traits to the next generation. The algorithm iterates through selection, crossover and mutation operators until convergence is reached.

1. An overview of Genetic Algorithm
By David Beasley, David R. Bull and Ralph R. Martin
090070T – T.P.K. Dahanayakage
090150N – K.M.T.V. Ganegedara

2. Introduction
 Population Evolves
 Natural Selection
 Survival of the fittest
 Applications?
 Computer, Bridges, Garment, etc.

3. Analogy
 Think about successive generations

4. Analogy (ctd)
Super-fit
 Evolve according to environment

5. Basic Concept
 Set of solutions for a problem
 Each solution – fitness score
 Reproduce a new set of solutions by
“Cross-breeding”
 Most-fit: get selected
 Least-fit: not selected – die out
 Result?
 Offsprings with characteristics from most-
fit

6. What just happened?
 Good characteristics of a generation
was spread in a successive
generation
 Most promising areas of solution
space are searched

7. Algorithm
BEGIN
Generate population
Calculate fitness for each individual
WHILE NOT CONVERGED DO
BEGIN
FOR population_size/2 DO
BEGIN
Select 2 parents for mating
Combine and produce an offspring
Calculate the fitness for the new individual
Insert the offspring to the new generation
END
END
END

8. Lesson on Biology
 Chromosome
 Organized collection of coiled DNA
DNA

9. Fitness function
 Must represent the “fitness to the
environment” or “ability” of a
chromosome’s
 Issues of fitness range
 Premature convergence
 Slow finishing

10. Reproduction
 Selection of parents
 Random
 Favors the fittest
 Crossover
 Single point crossover
 Cut 2 chromosomes at a random point
 Swap over tails to create 2 new chromosomes

11. Reproduction (ctd)
 Crossover is not the only case!
 0.6 - 1.0 chance
 Otherwise replicate the parent
 Mutation
 Alter the genes of crossover-ed with a
small probability

12. Example
0101001100 1011001001
0101001001 1011001100
Before mutation: 0 1 0 1 0 0 1 0 0 1
After mutation: 0101101001

13. Convergence
 Fitness of the BEST and AVERAGE
moves to a global optimum
 Gene is said to have converged
 95% of the population has converged
 Population is said to have converged
 All the genes have converged

14. Other techniques

15. “Schemata” and “Scheme”
 Definition of Schema
 Pattern of gene
 String comprise {0,1,#}
 Ex: Chromosome 0110 contains following
“Schemata”
 #110, #1#0, 01##, etc.
 A chromosome is said to contain a schema if
it matches a particular schemata

16.  Order of schema – Number of non-#
symbols
 Length of schema – Distance
between outer most non-# symbols.
 Ex: #1#0

17. Schema Theorem
 Individuals in a population are given reproductive
trials
 Number of trials α Fitness of an individual
 Higher fitness value -> Good schemata
 Good Schemata receives
exponentially increasing number of
trials in successive generations!

18. Building Block Hypothesis
 Definition
 Schemata short in length and tend to
improve performance when incorporated
to an individual
 Properties of a successful coding
scheme
 Related genes close together
 Little interaction between genes

19. Exploration and Exploitation
 Exploration
 Exploring unknown areas
 Exploitation
 Utilizing already-learnt to find better solutions
 Tradeoff
 Ex: Random search and Hill climbing
 GA combines both in an optimal way!

20. Practical Aspects of GA

21. Parent selection
 Individuals are copied to a “mating
pool”
 Highly fit – more copies
 Less fit – lesser copies
 How to determine number of copies?
 Explicit fitness remapping
 Implicit fitness remapping

22. Explicit fitness remapping
Individual’s fitness
Average fitness of population
 Issue: Number of copies should be an
integer
 Solution:
 Fitness scaling
 Fitness windowing

23. Implicit fitness remapping
 Tournament selection
 2 random individuals
 Copy the one with higher fitness value
to the mating pool
 Continue until the pool is full

24. Generation gaps and
steady-state replacement
 Generation gap
 Proportion of individuals in a population
replaced in each generation
 Steady-state replacement
 Only few individuals are replaced in a
generation
 Considerations:
 Parent selection – Random, Fitness
 Replacement – Random, Inverse fitness

25. Thank you
 Q & A Session