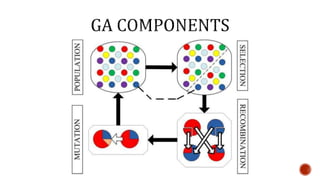
Genetic algorithms are a metaheuristic inspired by the process of natural selection that generates solutions to optimization and search problems. They use techniques like inheritance, mutation, selection, and crossover to evolve a population of solutions over multiple generations towards better solutions. Genetic algorithms represent potential solutions as chromosomes and evaluate their fitness to survive and reproduce, selecting the fittest to pass traits to the next generation.

2.  Search technique used in computing to find the true or approximate solutions to
optimization and search problems
 Categorized as global search heuristic
 Uses techniques inspired by evolutionary biology such as inheritance, mutation, selection,
crossover (also called recombination)
 Implemented as a computer simulation in which population of abstract representation
(chromosomes/ genotype/ genome) of candidate solutions (individual/ creatures) to an
optimization problem evolves towards a better solution
 Solutions are represented in binary but other encodings are also possible

3.  Evolution starts from a population of randomly generated individuals and happens in
generations
 In each generation, the fitness of every individual is evaluated, multiple individuals are
selected form current population and modified to form a new population
 The new population is then used in the next iteration of the algorithm
 The algorithm terminates when the desired number of generation has been produced or a
satisfactory fitness level has been reached

4.  Individual – any possible solution
 Population – group of all individuals
 Search space – all possible solution to the problem
 Chromosome – blueprint of an individual
 Trait – possible aspect of an individual
 Allele – possible setting of a trait
 Locus – position of gene on the chromosome
 Genome – collection of all chromosomes for an individual

5.  Cells are the basic building block of the body
 Each cell has a core structure that contains the chromosomes
 Each chromosome is made up of tightly coiled strands of DNA
 Genes are segments of DNA that determine specific traits such as eye or hair colour
 A gene mutation is an alteration in DNA. It can be inherited or acquired during lifetime
 Darwin’s theory of evolution – only the organism best adapted to heir environment tend
to survive

6.  Produce an initial population of individuals
 Evaluate the fitness of all individuals
 While termination condition not meet do
 Select filter individuals for reproduction
 Recombine between individuals
 Mutate individuals
 Evaluate the fitness of modified individuals
 Generate a new population
 End while

8.  Suppose we want to maximize the number of ones in a string of L binary digits
 An individual is encoding as a string of l binary digits
 Lets say L = 10, so 1 = 0000000001 (10 bits)

9. Produce an initial population of individuals
 Evaluate the fitness of all individuals
 While termination condition not meet do
 Select filter individuals for reproduction
 Recombine between individuals
 Mutate individuals
 Evaluate the fitness of modified individuals
 Generate a new population
 End while

10.  We start with the population of n random string. Suppose that l = 10 and n = 6
 We toss a fair coin 60 times to get the following initial population
s1 = 1111010101 f (s1) = 7
s2 = 0111000101 f (s2) = 5
s3 = 1110110101 f (s3) = 7
s4 = 0100010011 f (s4) = 4
s5 = 1110111101 f (s5) = 8
s6 = 0100110000 f (s6) = 3

11.  Produce an initial population of individuals
Evaluate the fitness of all individuals
 While termination condition not meet do
 Select filter individuals for reproduction
 Recombine between individuals
 Mutate individuals
 Evaluate the fitness of modified individuals
 Generate a new population
 End while

13.  Generates and combines multiple predictions
 Bagging: Bootstrap Aggregating
 Boosting
 Tends to get better results since there is deliberately introduced significant diversity
among models
 Bagging and boosting are meta-algorithms that pool decisions from multiple classifiers

14.  Improves stability and accuracy of machine-learning algorithms used in statistical
classification and regression
 Reduces variance and helps avoid overfitting
 Technique: given a standard training set D of size n, bagging generates m new training
set Di each of size n’ by sampling from D uniformly and with replacement
 If n’=n, then for large n, the set Di is expected to have the fractions of unique examples of
D, the rest being duplicates

15.  Lets calculate the average price of a house
 From F, get a sample x = (x1, x2, …, xn) and calculate the average u
 Now get several samples from F
 Its impossible to get multiple samples. So we use bootstrap
 Repeat B time:
 Generate a sample Lk of of size n from L by sampling with replacement
 Compute x* for x
 We now have bootstrap values
 X* = (x1*, ……., x2*)

16. X=(3.12, 0, 1.57,
19.67, 0.22, 2.20)
Mean=4.46
X1=(1.57,0.22,19.67,
0,0,2.2,3.12)
Mean=4.13
X2=(0, 2.20, 2.20,
2.20, 19.67, 1.57)
Mean=4.64
X3=(0.22, 3.12,1.57,
3.12, 2.20, 0.22)
Mean=1.74

17.  Based on the question: can a set of weak learners produce a strong learners?
 Weak learner is a classifier that is strongly related to true classification
 Strong learner is a classifier that is well-correlated with true classification