This document summarizes a lecture on game theory given by Dr. D. B. Naik. The lecture covers the key concepts of game theory including the definition of a game, two-person zero-sum games, saddle points, pure and mixed strategies, dominance rules, solving for the value of a game using algebraic and graphical methods, and approximate iterative methods. Solution techniques discussed include sub-games, linear programming, and the simplex method. The document provides examples to illustrate the various game theory concepts and solution approaches.

1. Lecture
on
“Game Theory”
By
Dr. D. B. Naik (Ph.D. - Mech. Engg.),
Professor & Head,
Training & Placement Section,
Sardar Vallabhbhai National Institute
of Technology, Surat, Gujarat, India

2. Topics to be covered :
(1) What is a game ?
(2) “Two Person Zero Sum” game
(3) Solution of game means ?
(4) Saddle Point
(5) Pure Strategy and Mixed Strategy
(6) Dominance Rule

3. (7) Value of game for given Mixed Strategies of both
players
(8) Algebraic Method for 2x2 Mixed Strategy game
problems
(9) Methods to solve 2xN or Nx2 games :
[a] Method of sub-games
[b] Graphical Method
(10) Application of LP to solve game problem
(11) Iterative / Approximate Method to solve game
problem

4. [ 1 ] What is a game ?
B
1 2 ……………. n
1
2
A .
.
m
Pij
Aim of A is to get maximum
A’s payoffs / gains
(Payoff Matrix)
Aim of B is to see that A gets minimum
Game Problems are problems of “Decision Making
Under Conflicts” or “Decision Making Under
Competitive Situations”.

5. [ 2 ] “Two Person Zero Sum” game
( i ) Two competitors.
( ii ) Finite number of strategies by both players.
( iii ) Play of game results when each competitor
chooses a single strategy or combination of
strategies.
( iv ) After both have chosen strategy / strategies,
their respective gains are finite.
( v ) Gain of one will be loss of other.
( vi ) Gain of a competitor depends on his action
as well as action of opponent.

6. [ 3 ] Solution of game means ?
( 1 ) Optimal (Best) strategies by both players.
( 2 ) Value of game when both players choose
optimal strategies.
V *
= Optimal value of game
= Expected gain of A if both the players use
their best strategies.

7. [ 4 ] Saddle Point :B
1 2 3 4
1
A 2
3
−5 3 1 20
5 5 4 6
−4 −2 0 −6
Minima
−5
4
−6
5Maxima 5 4 20
Maximin
Minimax
(Maximum out of
Minimums.)
(Minimum out of
Maximums.)
Saddle Point is P23
∴ V* = 4

8. Saddle Point definition :
It is an element of a matrix that is both the lowest
element in its row and the highest element in its
column.
It can be defined as an element of matrix that is at
once the largest of row minima and the smallest of
column maxima.
OR

9. [ 5 ] Pure Strategy and Mixed Strategy
1 2
2 3
1
2
2 3
∴ V = 2
Pure Strategy Case
1 8
6 4
1
4
6 8
∴ 4 ≤ V ≤ 6
Mixed Strategy Case

10. [ 6 ] Dominance Rule
Dominance Rule is applied to reduce the size of game
problem.
j
i
k
If Pij ≥ Pkj for each j then
kth
strategy of A is deleted.
≤

11. j k
i
If Pij ≥ Pik for each i then
jth
strategy of B is deleted.
≥

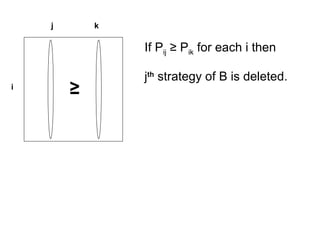
12. [ 7 ] Value of game for given Mixed
Strategies of both players
B
(y1) (y2) (y3) (y4)
1 2 3 4
(x1) 1
A (x2) 2
(x3) 3
Pij
Mixed Strategy 3x4 game problem :
x1 + x2 + x3 = 1
y1 + y2 + y3 + y4 = 1

13. B
(y1) (y2) (y3) (y4)
1 2 3 4
(x1) 1
A (x2) 2
(x3) 3
Pij
V = P11 x1 y1 + P12 x1 y2 + P13 x1 y3 + P14 x1 y4
+ P21 x2 y1 + P22 x2 y2 + P23 x2 y3 + P24 x2 y4
+ P31 x3 y1 + P32 x3 y3 + P33 x3 y3 + P34 x3 y4

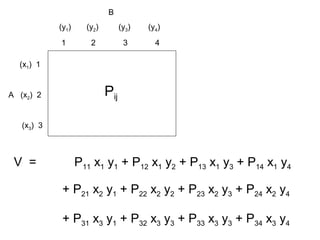
14. [ 8 ] Algebraic Method for 2x2 Mixed
Strategy game problems
P11 P12
P21 P22
y1 y2
x1
x2
P11 x1 + P21 x2 ≥ V
P12 x1 + P22 x2 ≥ V
x1 + x2 = 1
P11 y1 + P12 y2 ≤ V
P21 y1 + P22 y2 ≤ V
y1 + y2 = 1

15. ( )( )[ ] ( )( )[ ]
( ) ( ){ } ( ) ( ){ }[ ]12212211
12212211
PPPP
PPPP
V
+−+
−
=
( ) ( )
( ) ( )1211
2122
2
1
PP
PP
x
x
−
−
=
( ) ( )
( ) ( )2111
1222
2
1
PP
PP
y
y
−
−
=

16. 2 −1
−2 1
2 1
Solve following Game Problem :
−1
−2
−1 ≤ V ≤ 1
∴ Mixed Strategy
( )( )[ ] ( )( )[ ]
( ) ( ){ } ( ) ( ){ }[ ]2112
2112
−+−−+
−−−
=V
( ) ( )
( ) ( )12
21
2
1
−−
−−
=
x
x
( ) ( )
( ) ( )22
11
2
1
−−
−−
=
y
y
0
5
0
==
1
1
3
3
== ∴ x1 = ½, x2 = ½
2
1
4
2
== ∴ y1 = 1/3, y2 = 2/3

17. [ 9 ] Methods to solve 2xN or Nx2 games :
[a] Method of sub-games
[b] Graphical Method
[a] Method of sub-games :
1
2
3
1 2
2 4
3 2
-2 6
2
2
-2
3 6
∴ 2 ≤ V ≤ 3
∴ Mixed Strategy
Dominance Rule
not applicable.

18. 1
2
3
1 2
2 4
3 2
-2 6
1 2 1 2 1 2
1
2
1
3
2
3
Sub games :
2 4
3 2
2
2
3 4
∴ 2 ≤ V ≤ 3
2 4
-2 6
2
-2
2 6
∴ V = 2
3 2
-2 6
2
-2
3 6
∴ 2 ≤ V ≤ 3

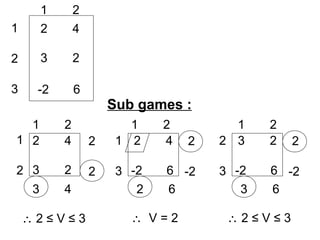
19. 1 2
1 2
1 2
1
2
1
3
2
3
2 4
3 2
2
2
3 4
2 4
-2 6
2
-2
2 6
3 2
-2 6
2
-2
3 6
( )( )[ ] ( )( )[ ]
( ) ( ){ } ( ) ( ){ }[ ]
66.2
3
8
4322
4322
==
+−+
−
=V
V = 2
( )( )[ ] ( )( )[ ]
( ) ( ){ } ( ) ( ){ }[ ]
44.2
9
22
2263
2263
==
+−−+
−−
=V
∴V* = 2.66

20. Hence,
1 2
1
2
2 4 2
2
3 4
3 2
V* = 2.66
0,
3
2
,
3
1
2
1
42
32
321
2
1
===∴=
−
−
= xxx
x
x
3
1
,
3
2
1
2
32
42
21
2
1
==∴=
−
−
= yy
y
y

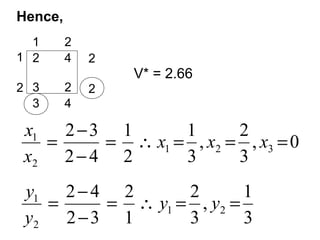
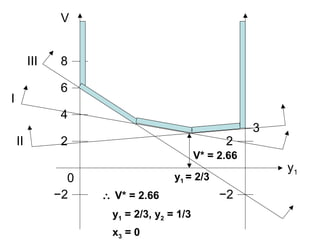
21. [b] Graphical Method
1
2
3
1 2
2 4
3 2
-2 6
2y1 + 4y2 ≤ V
3y1 + 2y2 ≤ V
−2y1 + 6y2 ≤ V
y1 + y2 = 1
∴ 2y1 + 4 (1−y1) ≤ V
3y1 + 2 (1−y1) ≤ V
−2y1 + 6 (1−y1) ≤ V
∴ V + 2y1 ≥ 4
V − y1 ≥ 2
V + 8y1 ≥ 6

22. 0
−2
2
4
6
8
−2
2
3
V
y1
V* = 2.66
y1 = 2/3
I
II
III
∴ V* = 2.66
y1 = 2/3, y2 = 1/3
x3 = 0

23. [ 10 ] Application of LP to solve game problem
−2 3 4
−1 4 −3
3 −4 5
3 4 5
−2
−3
−4
−2 ≤ V ≤ 3
Add +3 to each element

24. 1 6 7
2 7 0
6 −1 8
∴ 1 ≤ V ≤ 6
y1 y2 y3
1y1 + 6y2 + 7y3 ≤ V
2y1 + 7y2 + 0y3 ≤ V
6y1 − 1y2 + 8y3 ≤ V
y1 + y2 + y3 = 1
1
76 321
≤++
V
y
V
y
V
y
1
072 321
≤++
V
y
V
y
V
y
1
816 321
≤+−
V
y
V
y
V
y
VV
y
V
y
V
y 1321
=++

25. Max (1/V) = Y1 + Y2 + Y3
then
V
y
YIf ,=
s/t Y1 + 6Y2 + 7Y3 ≤ 1
2Y1 + 7Y2 + 0Y3 ≤ 1
6Y1 − 1Y2 + 8Y3 ≤ 1
Y1, Y2, Y3 ≥ 0
Solving this LPP we shall get :
Y1 = ___ Y2 = ___ Y3 = ___ 1/V = ___ ∴ V = ___
∴ y1 = ___ y2 = ___ y3 = ___ V = ___
∴ Vactual = V − 3

26. Now X1, X2, X3 will be dual variables of the
primal problem.
The values of X1, X2, X3 will be obtained from
final table of simplex of primal problem.
X1 = ___ X2 = ___ X3 = ___
∴ x1 = ___ x2 = ___ x3 = ___

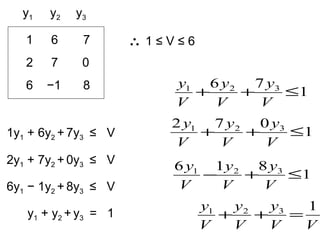
27. [ 11 ] Approximate method / Method of Iteration
1 6 7
2 7 0
6 −1 8

28. 1 6 7
2 7 0
6 −1 8
1
2
6
6 −1 8
13
16
4
7
9
5
20
16
12
21
18
18
22
20
24
23
22
30
29
29
29
30
31
35
36
38
34
3
3
4
8 6 8
10 13 8
11 19 15
12 25 22
18 24 30
24 23 38
25 29 45
31 28 53
33 35 53
5 4 1
Hence, 33/10 ≤ V*
≤ 38/10
x1 : x2 : x3 = 3 : 3 : 4
y1 : y2 : y3 = 5 : 4 : 1

29. Thank youThank you
For any Query or suggestion :
Contact :
Dr. D. B. Naik
Professor & Head, Training & Placement (T&P)
S. V. National Institute of Technology (SVNIT),
Ichchhanath, Surat – 395 007 (Gujarat) INDIA.
Email ID : dbnaik@gmail.com
dbnaik@svnit.ac.in
dbnaik_svr@yahoo.com
Phone No. : 0261-2201540 (D), 2255225 (O)