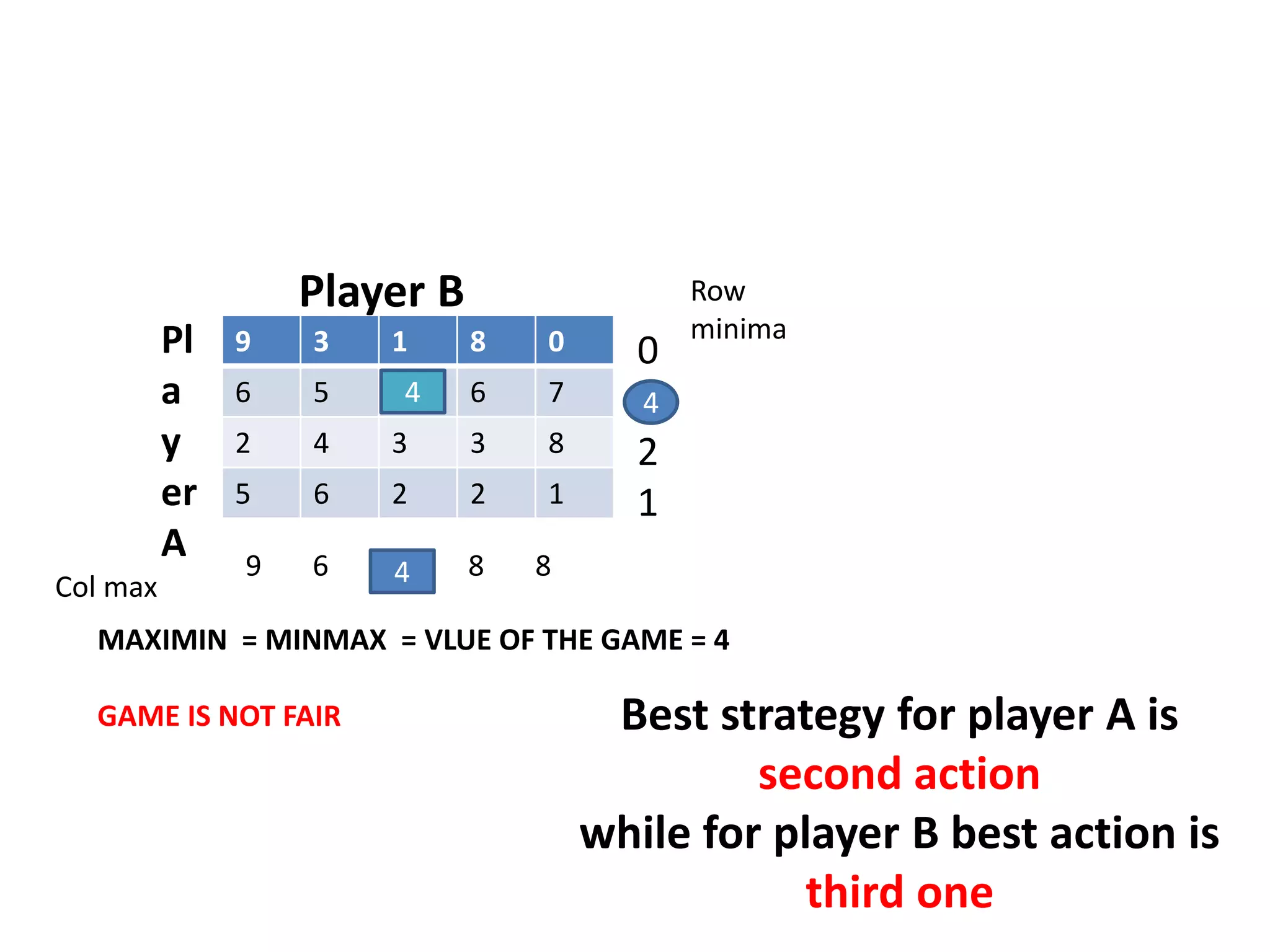
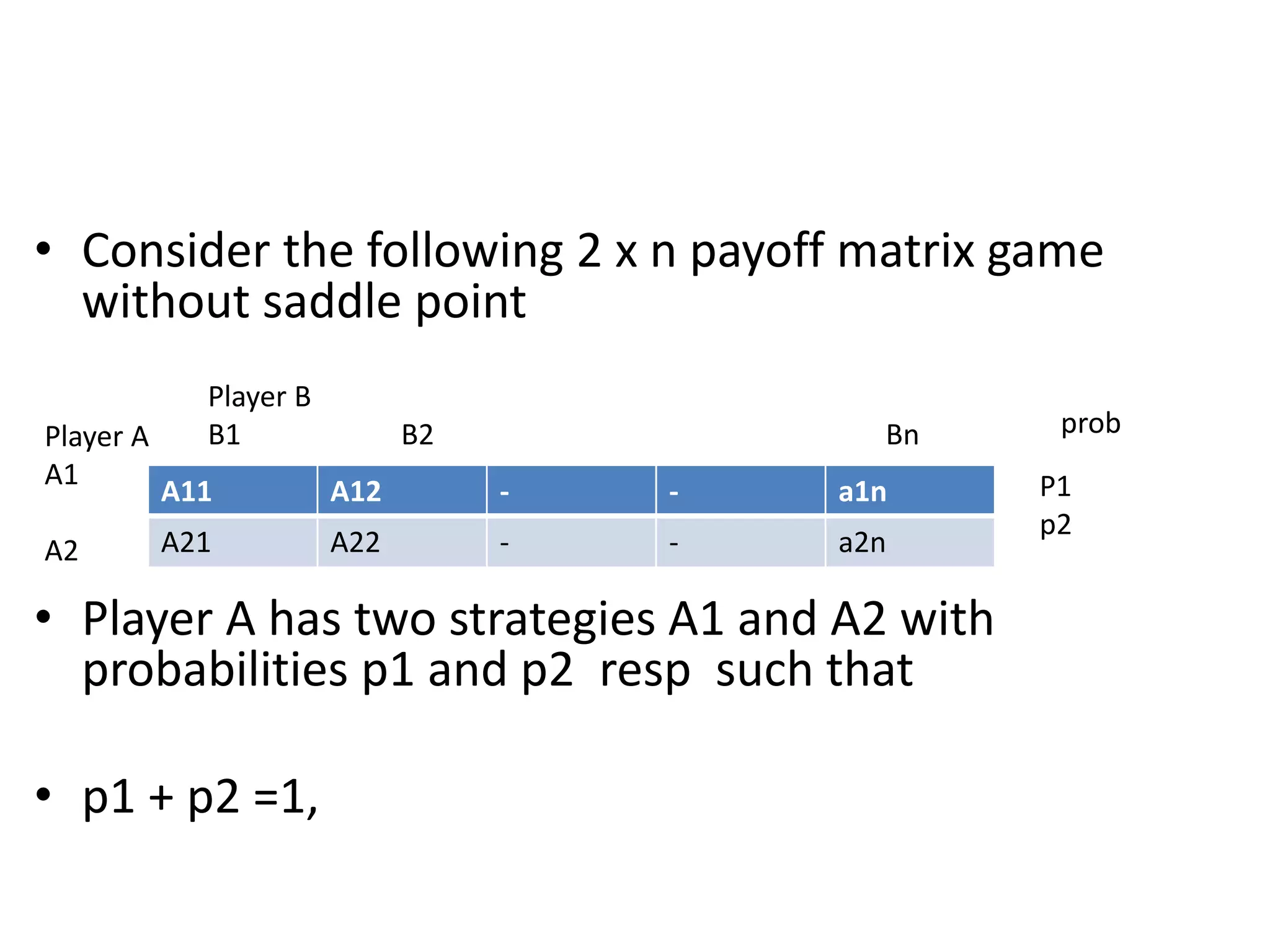
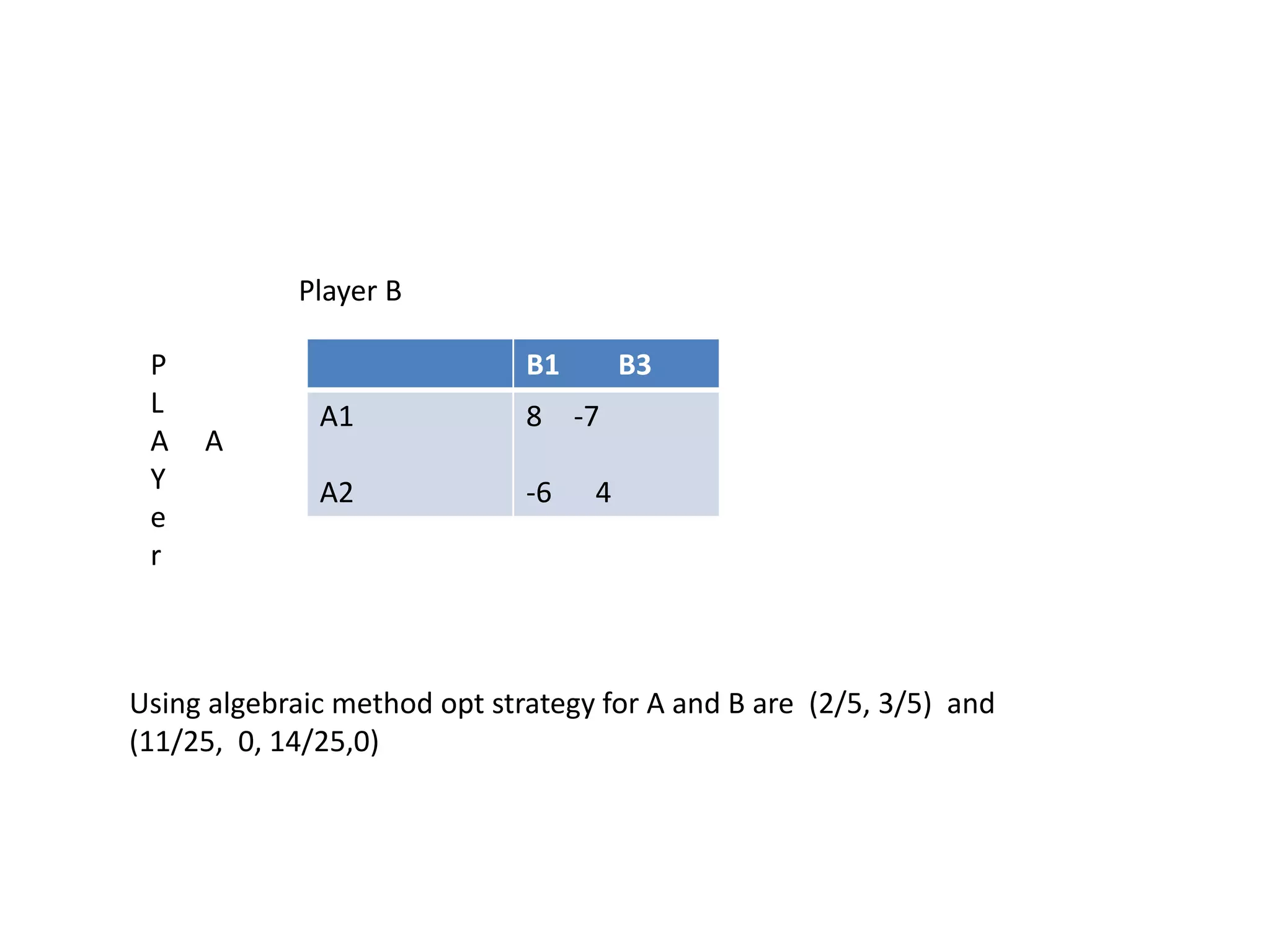
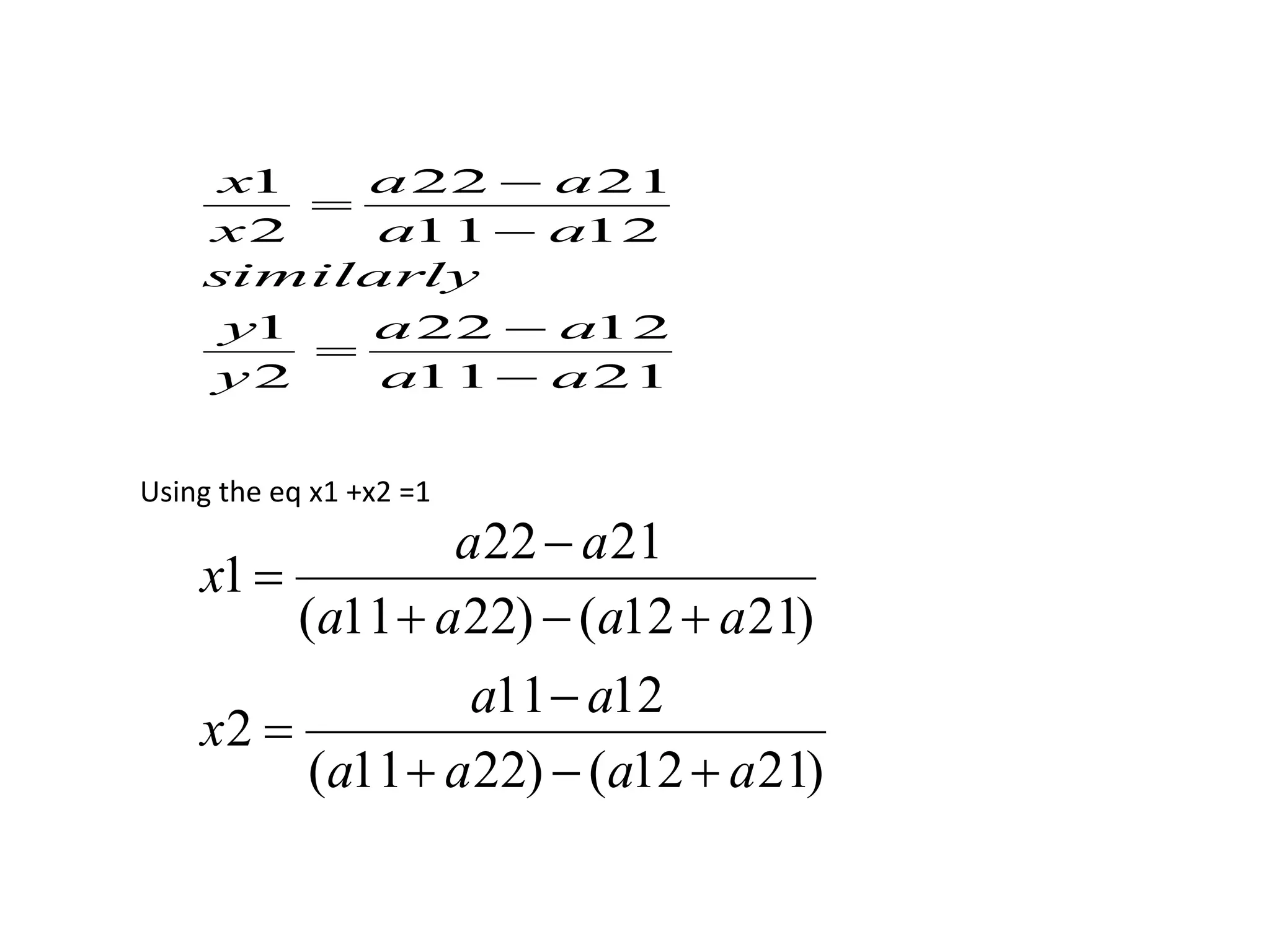This document discusses game theory and how to solve two-person zero-sum games. It explains that game theory models strategic interactions between parties with conflicting interests. A two-person zero-sum game is one where one player's gains equal the other's losses. Such games can be represented using a payoff matrix, from which optimal strategies and the value of the game can be determined. Techniques include finding pure and mixed strategies, saddle points, and using dominance rules and graphical methods to reduce larger games.

1. Game Theory

2. • Theory of games started in 20 th century,
developed by John Von Neumann and
Morgenstern

3. In many practical problems, it is required to take
decision in a situation where there are two or
more opposite parties with conflicting interests
and the action of one depends upon the action
which the opponent takes.

4. • A great variety of competitive situations are
commonly seen every day life
• e.g in military battles, political campaigns
marketing campaigns

5. Competitive games
Following properties
1- There are finite no of competitors
2- Each player has available to him a list of finite no
of possible courses of actions.
3 - A play is said to be played when each of the players
chooses a single course of action from the list.
Here it is assumed that the choices are made
simultaneously so that no player knows his
opponents choice until he has decided his own
course of action.
4 - Every play determines an outcome.

6. Two person Zero sum game
A game with only two players in which the gains
of one player are the losses of another player
is called two person zero sum game

7. Pay off matrix
• In a two person zero sum game the resulting gain can
be represented in the form of matrix called pay off
matrix.
• Suppose player A has m courses of action and B has n
courses of action.
• Pay off can be represented by m by n matrix
• Rows are of courses of action available for A
• columns are of courses of action available for B
• In A’s payoff matrix aij represents the payment to A
when A chooses action “i “and B chooses action” j”
• B’s pay off matrix will be negative of A’s pay off matrix

8. B
+1 -1
-1 +1
A
1 finger 2 finger
1 finger
2 fingers
A’s pay off matrix

9. Strategy
• The strategy of a player is the predetermined
rule
by which
• a player decides his course of action from his
own list of courses of action during the game

10. Pure / mixed strategies
A Pure strategy is a decision in advance of all plays,
always to choose a particular course of action
A mixed strategy is a decision in advance of all
plays,to choose a course of action for each play in
accordance with some particular probability
distribution.
Opponents are kept guessing as to which course of
action is to be selected by the other on any
particular occasion.
Pure strategy is a special case of mixed strategy.

11. Solution of a game
By solving a game we mean to find the best
strategies for both the players and the value of the
game.
Value of the game
Is the maximum guaranteed gain to player A (A maximixing
player) if both the players use their best strategies.
It is generally denoted by “v” and is unique.
Fair game : if the value of the game is zero.

12. Maximin and minimax criterion of
optimality
It states that if a player lists his worst possible
outcomes of all his potential strategies then
he will choose that strategy which
corresponds to the best of these worst
outcomes.

13. • Maxmin for A is given by max {min aij } = apq
I j
Minimax fo B min {max aij } = ars
j I
a pq ≤ a r s
Maximin for A ≤ minimax for B
If v is the value of the game
Maxmin for A ≤ v ≤ minimax for B

14. Saddle pint
• if minimax = maximin = value of the game then
game is called a game with saddle point.
Def: A saddle point of a pay off matrix is that
position in the matrix where the maximum of row
min’s coincides with the minimum of column ‘s
maxima.
The cell entry at that saddle point is called the
value of the game.
In a game with saddle point the players use pure
strategies i.e they choose the same course of
action through out the game

15. Method for detecting a saddle point
Find the minimum value in each row and write it in row
minima
Find the maximum value in each column and put it in
column maxima.
Select the largest element in row minima and enclose it in
circle and select the lowest element in column max and
encloses it in rectangle.
Find the element which is same in the circle and rectangle
and mark the position of such element in matrix..
It is the saddle point which represents the value of the
game.

16. Player B
9 3 1 8 0
6 5 4 6 7
2 4 3 3 8
5 6 2 2 1
Pl
a
y
er
A
Row
minima
0
4
2
1
4
9 6 4 8 8
4
4
Col max
MAXIMIN = MINMAX = VLUE OF THE GAME = 4
GAME IS NOT FAIR
Best strategy for player A is
second action
while for player B best action is
third one

17. Rules of dominance
Rule 1
if all the elements in a row (say I th)of payoff
matrix are less than or equal to the
corresponding elements of other row(say j th)
then player A will never choose the I th
strategy or in other words I th strategy is
dominated by the j th strategy.

18. Rule 2
• If all the elements in a column(say r th) of
payoff matrix are greater than or equal t o the
corresponding elements of other column (say
s th) then the player B will never choose the r
th strategy or in other words the r th strategy
is dominated by the s th strategy

19. Rule 3
• A pure strategy may be dominated if it is
inferior to an average of two or more other
pure strategies.

20. -1 -2 8
7 5 -1
6 0 12
No saddle point exists,
For A pure strategy I is dominated by strategy
III.
also for player B pure strategy I is dominated
by strategy II.

21. Solution of 2 x n or m x 2 games without
saddle point(graphical method)
• Either of the players has only two
undominated pure strategies available.
• By using graphical method it is aimed to
reduce a game to the order of 2 x 2 by
identifying and eliminating the dominated
strategies and then solve it by analytical
method.

22. • Consider the following 2 x n payoff matrix game
without saddle point
Player B
B1 B2 Bn Player A prob
A1
A11 A12 - - a1n
A21 A22 - - a2n
A2
• Player A has two strategies A1 and A2 with
probabilities p1 and p2 resp such that
• p1 + p2 =1,
P1
p2

23. • For each of the pure strategies available to
player B, expected payoff for player A would
be as follows:
Player B’s pure
strategy
Player A’s
expected payoff
B1
B2
-
-
Bn
a11 p1 + a21 p2
a12 p1 +a22 p2
a1n p1 +a2np2

24. According to the maximum criterion for mixed strategy
games player
A should select the value of probabilities p1,p2 to
maximize his minimum expected payoff.
This can be done by plotting st lines representing player
A’s expected payoffs. The highest point of the lower
boundary of these lines(lower envelope) will give
maximum expected payoff and the optimum values of
probabilities p1 and p2. Now the two strategies of player B
corresponding to those lines which pass through the
maximum point can be determined

25. • The m x 2 games are also treated in the same
way except that the upper boundary of the st
lines corresponding to B’s expected payoff
will give the maximum expected payoff to
player B and the lowest point on this
boundary (upper envelope) will then give the
minimum expected payoff and the optimum
values of prob q1 and q2.

26. Solve the game graphically with the
following payoff matrix
B1 B2 B3 B4
A1 8 5 -7 9
A2 -6 6 4 -2
When B chooses B1 expected payoff for A shall be
8 p1 + (-6)(1-p1) or 14 p1 -6
Similarly expected payoff functions in respect to
B2,B3 and B4 can be derived as
6-p1; 4- 11p1 ; 11 p1 -2 resp.
We can represent these graphically plotting each
payoff as a function of p1

28. • Lines are marked B1,B2,B3 and B4 and they
represent the respective strategies. For each
value of p1 the height of the lines at that point
denotes the payoff of each of B’s strategy
against (p1,1-p1) for A.A is concerned with his
least payoff when he plays a particular
strategy, which is represented by the lowest of
the four lines at that point and wishes to
choose p1 in order to maximize this minimum
payoff.

29. • This is at K where the lower envelope lowest
of the lines at his point is the highest. this
point lies at the intersection of the lines
representing B1 and B2 strategies.distance
• KL = -0.4 represents the game value V
• Alternatively the game can be written as a 2
by 2 game as follows with strategies A1 and
A2 for A and B1 and B3 for B

30. P
L
A A
Y
e
r
B1 B3
A1
A2
8 -7
-6 4
Player B
Using algebraic method opt strategy for A and B are (2/5, 3/5) and
(11/25, 0, 14/25,0)

31. Theorem
• For any zero sum two person game where the
optimum strategies are not pure and for
player A payoff matrix is A, the optimal
strategies are (x1,x2) and (y1,y2) given by
•
a a
22 
21
a a
22 
12
11 21
x
and
y
and thevalueof the gameto Ais
a a a a
11 22 
12 21
( 11 22) ( 12 21)
1
1
2
11 12
2
a a a a
v
a a
y
a a
x
  






32. If (x1,x2) and(y1,y2) are the mixed strategies for
players A and B resp then
x1 +x2 = 1
y1 + y2 = 1
x1≥ 0, x2 ≥0, y1 ≥ 0 , y2 ≥ 0

33. Expected gain to A when B uses strategy 1
a11 x1 + a21x2
Expected gain to A when B uses strategy II
a12 x1 + a22x2
Similarly expected loss for B when A uses strategy I
a11y1 +a12y2
Similarly expected loss for B when A uses strategy II
a21 y1+ a22 y2

34. • If v is the value of the game then
• since A expects to get at least v
• a11 x1 + a21x2 ≥ v
• a12 x1 + a22x2 ≥ v
• Also B expects atmost v
• a11y1 +a12y2≤v
• a21 y1+ a22 y2 ≤v

35. a11 x1 + a21x2=v
a12 x1 + a22x2 =v
a11y1 +a12y2=v
a21 y1+ a22 y2 =v
(a11 – a12 ) x1 = (a22-a21) x2

36. a a
21 22
x
similarly

a a
22

12 21 11
1
y
1
2
12 11
2
a a
y
a a
x




Using the eq x1 +x2 =1
a a
22 
21
a a
11 
12
( 11 22) ( 12 21)
2
( 11 22) ( 12 21)
1
a a a a
x
a a a a
x
  

  


37. similarly
a a
22 
12
a a
11 
21
( 11 22) ( 12 21)
2
( 11 22) ( 12 21)
1
a a a a
y
a a a a
y
  

  


38. Value of the game
a a a a
11 22 
12 21
a a a a
( 11 22) ( 12 21)
v
  


39. By using the dominance properties we always
try to reduce the size of payoff matrix to 2 x 2.
In case the payoff matrix reduces to size 2 x n or
m x 2 then graphical method is used

40. Q Solve the game whose payoff matrix
is
-1 -2 8
7 5 -1
6 0 12
No saddle point exists,
For A pure strategy I is dominated by strategy
III.
also for player B pure strategy I is dominated
by strategy II.

41. II III
5 -1
0 12
II
III
a a
22 
21
a a
11 
12
( 11 22) ( 12 21)
2
( 11 22) ( 12 21)
1
a a a a
x
a a a a
x
  

  

X1 = 2/3
X2 = 1/3

42. a a
22 
12
a a
11 
21
( 11 22) ( 12 21)
2
( 11 22) ( 12 21)
1
a a a a
y
a a a a
y
  

  

Y1 = 13/18
Y2 =5/18

43. a a a a
11 22 
12 21
a a a a
( 11 22) ( 12 21)
v
  

Value of the game is 10/3
Thus optimal strategy for A is (0,2/3 1/3)
And
For B (0,13/18,5/18)
Value of the game for A is 10/3

44. Q: solve the game whose pay off
matrix is
I Ii Iii iv
I 1 3 -3 7
II 2 5 4 -6