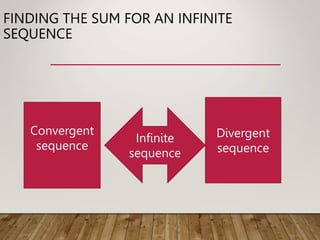
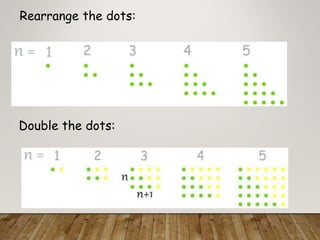
The document discusses the concept of patterns and sequences in mathematics, explaining how to identify patterns in numerical sequences to predict subsequent numbers. It also introduces finite and infinite sequences, as well as the general term for sequences, and touches upon series as sums of sequences. Additionally, examples and rules for determining the nth term of sequences are provided, along with discussions on convergent and divergent infinite sequences.

1. PATTERN
Objective:
generates patterns.
M10AL-Ia-1

3. IS THIS A PATTERN?
2,4,6,8,10,12,…
a, b, c, d, e

5. Patterns and sequences
We often need to spot a pattern in order to
predict what will happen next.
In maths, the correct name for a pattern of
numbers is called a SEQUENCE.
The first number in a SEQUENCE is sometimes
called the FIRST TERM; the second is the
SECOND TERM and so on.

6. Patterns and sequences
For any pattern it is important to try to spot
what is happening before you can predict the
next number.
The first 2 or 3 numbers is rarely enough to
show the full pattern - 4 or 5 numbers are
best.

7. Patterns and sequences
For any pattern it is important to try to spot
what is happening before you can predict the
next number.
1, 2, …… What’s the next number?

8. Patterns and sequences
For any pattern it is important to try to spot
what is happening before you can predict the
next number.
1, 2, 4,… Who thought that the next
number was 3?
What comes next?

9. Patterns and sequences
For any pattern it is important to try to spot
what is happening before you can predict the
next number.
1, 2, 4, 8, 16, …
What comes next?

10. Patterns and sequences
Look at what is happening from 1 TERM to
the next. See if that is what is happening
for every TERM.
5, 8, 12, 17, 23, …, …
+ 3

11. Patterns and sequences
Look at what is happening from 1 TERM to
the next. See if that is what is happening
for every TERM.
5, 8, 12, 17, 23, …, …
+ 3 + 4

12. Patterns and sequences
Look at what is happening from 1 TERM to
the next. See if that is what is happening
for every TERM.
5, 8, 12, 17, 23, …, …
+ 3 + 4

13. Patterns and sequences
Look at what is happening from 1 TERM to
the next. See if that is what is happening
for every TERM.
5, 8, 12, 17, 23, …, …
+ 3 + 4 + 5

14. Patterns and sequences
Look at what is happening from 1 TERM to
the next. See if that is what is happening
for every TERM.
5, 8, 12, 17, 23, …, …
+ 3 + 4 + 5 + 6

15. Patterns and sequences
Look at what is happening from 1 TERM to
the next. See if that is what is happening
for every TERM.
5, 8, 12, 17, 23, 30, …
+ 3 + 4 + 5 + 6 + 7

16. Patterns and sequences
Now try these patterns:
3, 7, 11, 15, 19, …, …
128, 64, 32, 16, 8, …, …
1000, 100, 10, 1, …, …
5, 15, 45, 135, …, …
Infinite
sequence
So what is a
finite sequence?

17. IN GENERAL,
•

18. CONSIDER THE FOLLOWING SEQUENCE
• 1, 4, 9, 16, 25, …
• What is the value of a (T1 ) ?
• T5 ?
• What is the pattern?
• T1 = 1 = 12
• T2 = 4 = 22
• T3 = 9 = 32
• … T12 = ?
• Tn = ?
Tn is
called
the
general
term
Sequence is

19. EXAMPLES: WRITE A RULE FOR THE NTH TERM.
•
•
,...
625
2
,
125
2
,
25
2
,
5
2
.
a
,...
5
2
,
5
2
,
5
2
,
5
2
4
3
2
1
,...
9
,
7
,
5
,
3
.
b
Look for a pattern…

20. EXAMPLE: WRITE A RULE FOR THE NTH TERM.
•
Think:

21. Describe the pattern, write the next term, and
write a rule for the nth term of the sequence
(a) – 1, – 8, – 27, – 64, . . .
SOLUTION
You can write the terms as (– 1)3, (– 2)3, (– 3)3,
(– 4)3, . . . . The next term is a5 = (– 5)3 = – 125.
A rule for the nth term is an = (– n)3.
a.

22. Describe the pattern, write the next term, and
write a rule for the nth term of the sequence
(b) 0, 2, 6, 12, . . . .
SOLUTION
You can write the terms as 0(1), 1(2), 2(3), 3(4),
. . . .
The next term is f (5) = 4(5) = 20. A rule for the
nth term is f (n) = (n – 1)n.
b.

23. CONSIDER THIS:
• What is the pattern? How many dots for the next term?
• What about the 50th term?
• Need to find general term or the rule first.
…

24. Rearrange the dots:
Double the dots:

25. THUS;
•

26. WRITE IN GENERAL TERM
•5,8,11,14, 17, …
•25, 21, 17, 13, …
•1, 3, 9, 27

27. SERIES
• A series is the sum of the terms in the
sequence and is represented by Sn.
• E.g.
• Sn = T1 + T2 + T3 +…+ Tn
• For finite series,
• 1 + 3 + 5 + 7.
• For infinite series,
• 1 + 2 + 3 + 4 +…

28. THE SUMMATION SYMBOL
•

29. GENERALLY.
• For finite series
• For infinite series,

30. WRITE THE FOLLOWING SERIES USING THE
SUMMATION SYMBOL
•

31. FINDING THE VALUES OF THE SUMMATION
•
1
+2+3+4+5+6+7+8+9+1
0
= 55
= 62
[2(-1) -3] + [2(0)-3]+[2(1)-3]
+[2(2)-3]
= -8

32. FINDING THE SUM FOR AN INFINITE
SEQUENCE
Infinite
sequence
Convergent
sequence
Divergent
sequence

33. CONVERGENCE
•

34. DIVERGENCE
•

35. Classify the following sequences as
Finite Sequence or Infinite sequence.
________________1. {1, 3, 5, 7, 9,…}
________________2. { 2, 4, 6, 8, 10}
________________3{ 2, -4, 6, -8, 10, …}
________________4. { 3, 6, 9, 12, 15 }
________________5. { 1, 4, 7, 10, 13 }

36. Content, graphics and text
belong to the rightful owner.
No copyright intended.