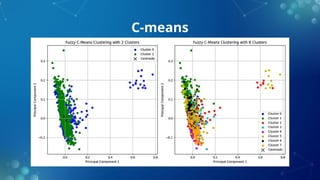
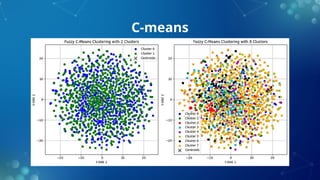
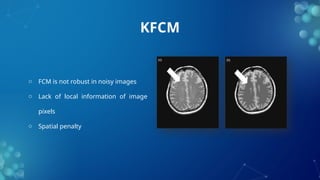
The document discusses fuzzy clustering, a method that allows data points to belong to multiple clusters with varying degrees of membership, contrasting it with traditional clustering methods like k-means. It outlines the benefits of fuzzy clustering, including increased accuracy and flexibility in data analysis, and describes algorithms such as fuzzy c-means, which enhances clustering precision for complex datasets. Additionally, it covers applications of fuzzy clustering in fields like medical imaging and bioinformatics, as well as the pros and cons of the method.

1. 9
0
7
3
5
1
2
4
Fuzzy Clustering
Zahra Mojtahedin
Learning Brain Machine 1

2. Table of contents
01
03
02
04
Fuzzy Clustering
Goals of Fuzzy
Clustering
K-means (Review)
05
07
06
08
C-means
Fuzzy Clustering
Application
Pros and Cons
KFCM
Iris Dataset
Segmentation

3. Fuzzy Clustering
01
Fuzzy clustering allows data points to belong to multiple
clusters with varying degrees of membership.
9
0
7
3
5

4. Fuzzy Clustering
Definition:
o Allows each data point to belong to multiple clusters with varying degrees of
membership.
o It differs from traditional clustering, where each data point belongs to exactly one
cluster.
Membership Degrees:
o Each data point has a set of membership degrees to different clusters.
o The sum of these membership degrees equals 1.
Unsupervised Learning:
o Fuzzy clustering is an unsupervised learning method.
o The model groups data without using predefined labels.
Benefits:
o Flexibility in partitioning data.
o Ability to assign a data point to multiple clusters.
o Efficient when boundaries between clusters are not clearly defined.
o Allows for nuanced analysis and better handling of uncertainty and overlap in data.

5. Crisp & Fuzzy Cluster
Crisp Clustering:
o Each data point belongs
to exactly one cluster.
o The boundaries between
clusters are clear and
distinct.
o Data points have binary
membership: either they
belong to a cluster, or
they do not.
o Example of crisp
clustering: K-Means
algorithm.
Fuzzy Clustering:
o Each data point can belong
to multiple clusters with
varying degrees of
membership.
o The boundaries between
clusters are vague and
flexible.
o Data points have relative
membership, meaning they
have varying degrees of
belonging to different
clusters.
o Example of fuzzy clustering:
Fuzzy C-Means algorithm.

6. Goals of Fuzzy Clustering
02
The primary goal of fuzzy clustering is to identify patterns in data
with increased accuracy and flexibility.
9
0
7
3
5

7. Goals of Fuzzy Clustering
o Pattern recognition: Fuzzy clustering helps us identify patterns in
data. This is particularly useful in cases where data points are not
clearly separable.
o Increased accuracy: By using fuzzy clustering, we can increase
the accuracy of analyses because this method allows a data point to
belong to multiple clusters.
o Reduced complexity: Fuzzy clustering can help reduce the
complexity of predictive models, as it provides more precise
information about the relationships between data points.
o Greater flexibility: This method offers greater flexibility in data
analysis, as it allows each data point to belong to multiple clusters.
0
7
5
8
6

8. K-means
03
is a crisp clustering algorithm, meaning each data point is assigned
to exactly one cluster without overlapping or partial memberships.
9
0
7
3
5

9. K-means
K-Means Clustering is one of the most commonly used algorithms in unsupervised
machine learning for partitioning a dataset into distinct clusters. This algorithm
assigns each data point to one of K clusters by minimizing the within-cluster
variance.

10. K-means
o Choosing the Number of Clusters: Decide on the number of clusters, to partition the data.
This is typically based on prior knowledge or by using methods like the elbow method.
o Initialization of Centroids: Randomly select K data points from the dataset as the initial
cluster centroids.
o Assigning Data Points to Clusters: Each data point is assigned to the nearest centroid,
forming K clusters. The distance metric commonly used is the Euclidean distance.
o Updating Centroids: Recalculate the centroid of each cluster by taking the mean of all data
points assigned to that cluster. The centroid is the new center of the cluster.
o Iterating Until Convergence: Steps 3 and 4 are repeated until the centroids no longer
change significantly, indicating that the algorithm has converged.

11. K-means
o Objective Function: The objective of K-means is to minimize the sum of squared distances
between data points and their respective cluster centroids. This can be formulated as:
where:
 is the number of clusters.
 represents the i-th cluster.
 x is a data point in cluster .
 is the centroid of cluster .
𝐽=∑
𝑖=1
𝑘
∑
𝑥∈𝐶𝑖
¿|𝑥−𝜇𝑖|∨¿2
¿

12. K-means
o Cluster Assignment Step: Assign each data point to the cluster with the nearest centroid:
 where is the cluster assignment for data point .
o Centroid Update Step: Update the centroid of each cluster by calculating the mean of all data
points assigned to that cluster:
 where is the number of data points in cluster .
∣∣
𝑐 𝑗=𝑎𝑟𝑔 min
𝑘
¿|𝑥− 𝜇𝑖|∨¿2
¿
𝜇𝑖=
1
|𝐶𝑖|
∑
𝑥𝑗 ∈𝐶 𝑗
𝑥 𝑗

13. C-means
04
An algorithm that assigns data points to clusters with varying
degrees of membership, enhancing flexibility and precision in
clustering.
9
0
7
3
5

14. C-means
Fuzzy C-Means (FCM) is an unsupervised learning algorithm that allows each data
point to belong to multiple clusters with varying degrees of membership. This
approach is particularly useful for analyzing complex and non-separable data. FCM
clustering is a soft clustering approach, where each data point is assigned a
likelihood or probability score belonging to that cluster.

15. C-means
1. Initialization:
o Determine the number of clusters () and the fuzziness parameter ().
o Initialize the membership matrix () with random values, where indicates the
membership degree of data point ii in cluster .
2. Compute Cluster Centers:
o Calculate the cluster centers using the following formula:
o where is the data point i and is the total number of data points.

16. C-means
3. Update Membership Matrix:
o Update the membership degrees using the following formula:
4. Check for Convergence:
o If the change in the membership matrix is less than a specified threshold (e.g., ), the algorithm stops.
ϵ
Otherwise, go back to step 2.

17. C-means

18. C-means

19. Fuzzy Clustering
Application
05 9
0
7
3
5

20. 0
7
5
8
6
2
4
9
0
Fuzzy Clustering Application
Image Segmentation:
o Medical Imaging: Helps in segmenting different tissues or detecting anomalies in
medical images.
o Satellite Imaging: Used in classifying land use and land cover from satellite images.
Pattern Recognition:
o Handwriting Recognition: Distinguishes between different styles of handwriting.
o Voice Recognition: Classifies different voice patterns for speaker identification.
Bioinformatics:
o Gene Expression Data: Clusters gene expression data to identify patterns and
understand gene functions.
o Protein Structure Analysis: Groups similar protein structures for comparative analysis.

21. Iris Dataset
Segmentation
06 9
0
7
3
5

22. Iris Dataset
o Origin: The dataset was introduced by British biologist and statistician Ronald A. Fisher in his
1936 paper "The use of multiple measurements in taxonomic problems".
o Content: It contains 150 samples from three species of iris flowers (Iris setosa, Iris versicolor, and
Iris virginica).
o Features: Each sample has four features:
Sepal length (in centimeters) Sepal width (in centimeters)
Petal length (in centimeters) Petal width (in centimeters)
o Classes: There are three classes, each corresponding to one species of iris flower (50 samples per
class).

23. Iris Dataset

24. Iris Dataset

25. KFCM
07 9
0
7
3
5

26. KFCM
o FCM is not robust in noisy images
o Lack of local information of image
pixels
o Spatial penalty

27. Pros and Cons
08 9
0
7
3
5

28. 0
7
3
5
Pros and Cons
Pros
o Gives best result for overlapped data set and comparatively better then k-means algorithm.
o Unlike k-means where data point must exclusively belong to one cluster center here data
point is assigned membership to each cluster center as a result of which data point may
belong to more then one cluster center.
Cons
o Apriori specification of the number of clusters.
o With lower value of β we get the better result but at the expense of more number of
iteration.
o Euclidean distance measures can unequally weight underlying factors.
o The performance of the FCM algorithm depends on the selection of the initial cluster center
and/or the initial membership value.

29. ● J. C. Dunn (1973): 'A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact
Well-Separated Clusters', Journal of Cybernetics 3: 32-57
● J. C. Bezdek (1981): 'Pattern Recognition with Fuzzy Objective Function Algorithms', Plenum
Press, New York
● Tariq Rashid: 'Clustering'
● Hans-Joachim Mucha and Hizir Sofyan: 'Nonhierarchical Clustering'
● http://www.cs.bris.ac.uk/home/ir600/documentation/fuzzy_clustering_initial_report/node11.
html
● http://www.quantlet.com/mdstat/scripts/sg/ssd/html/sgshiftclumei149.html
References

30. Thanks for your attention!