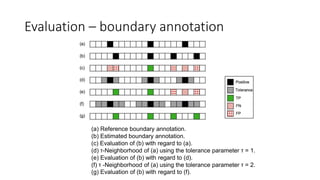
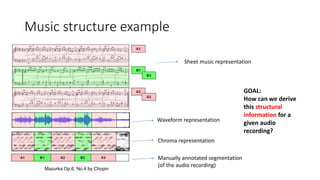
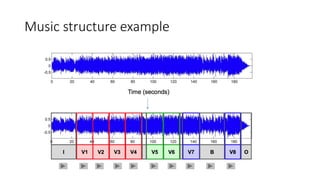
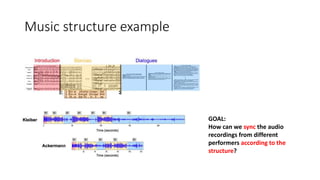
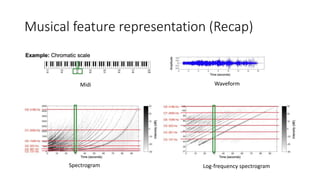
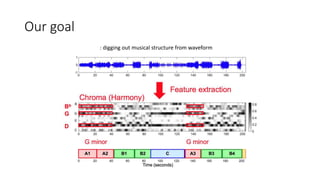
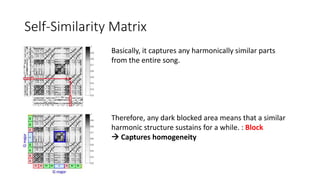
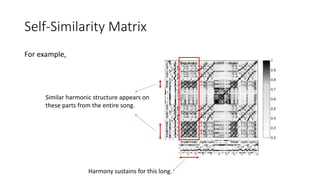
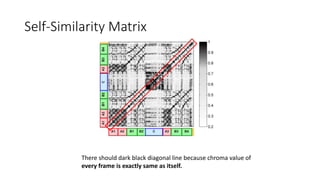
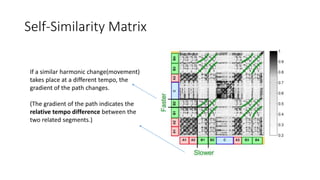
This document summarizes key aspects of chord recognition and music structure analysis from the book "Fundamentals of Music Processing". It discusses template-based and HMM-based chord recognition methods. For music structure analysis, it describes how a self-similarity matrix can be used to identify repetitive patterns in a song that correspond to musical parts or forms. Techniques are presented for enhancing the self-similarity matrix such as path smoothing, transposition invariance, and thresholding. Audio thumbnailing is introduced as a way to automatically select a representative section of a song using a fitness measure that balances repetitiveness and coverage of the song.

1. Review on ‘Fundamentals of Music Processing’
Ch.5 Chord recognition
모두의 연구소
Music processing lab
최정

2. So far we’ve covered..
• Music representations (ch1)
: basic notations/representations, their structure
• Fourier analysis (ch2)
: transforming signal into the Frequency domain(spectrogram),
sampling/DFT, FFT, STFT
• Music Synchronization (ch3)
: log-frequency spectrogram, Chromagram,
synchronization between different representation(DTW)
• Music Structure Analysis (ch4)
: Chroma-based self-similarity matrix  path, block(+ enhancements)
Audio thumbnailing (fitness function  optimization(DP)), Scape plot representation

3. Chapter 5: Chord Recognition
5.1 Basic Theory of Harmony
5.2 Template-Based Chord Recognition
5.3 HMM-Based Chord Recognition
5.4 Further Notes

4. Music structure analysis
The general goal of music structure analysis
: to divide a given music representation into temporal segments that
correspond to musical parts and to group these segments into
musically meaningful categories.
Examples of musically meaningful segmentation:
- Stanzas of a folk song
- Intro, verse, chorus, bridge, outro sections of a pop song
- Exposition, development, recapitulation, coda of a sonata
- Musical form ABACADA ... of a rondo

5. Music structure example
Mazurka Op.6, No.4 by Chopin
Sheet music representation
Waveform representation
Chroma representation
Manually annotated segmentation
(of the audio recording)
GOAL:
How can we derive
this structural
information for a
given audio
recording?

6. Music structure example

7. Music structure example
GOAL:
How can we sync the audio
recordings from different
performers according to the
structure?

8. Challenges..
Challenge: There are many different principles for creating
relationships that form the basis for the musical structure.
 Homogeneity: Consistency in tempo, instrumentation, key, ...
 Novelty: Sudden changes, surprising elements ...
 Repetition: Repeating themes, motives, rhythmic patterns,...
We’ll try to get structure out based on these principals.

9. In case of image processing(segmentation)..

10. Musical feature representation (Recap)
Midi Waveform
Spectrogram Log-frequency spectrogram

11. Musical feature representation (Recap)
Spectrogram Chromagram
Chromagram on chromatic scale

12. Our goal
: digging out musical structure from waveform

13. Self-Similarity Matrix
• Remember in chapter 3, we compared 2 different recordings by their
chromagram.
Cost : cosine distance
between 2 chroma vectors
(12 dimensional)

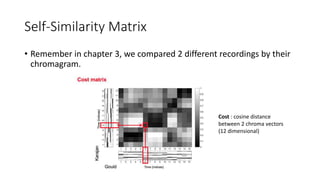
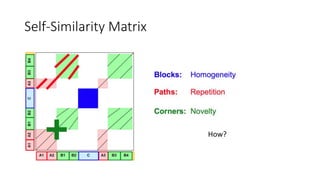
14. Self-Similarity Matrix
• SSM is doing a similar thing, but with itself this time.
Score of the cell (x, y) : similarity measure s(x, y)
(absolute value of the inner product)
N-square self-similarity matrix S ∈ RN×N
Where xn,xm ∈F (feature space), n,m∈[1:N]

15. Self-Similarity Matrix
How?

16. Self-Similarity Matrix
Basically, it captures any harmonically similar parts
from the entire song.
Therefore, any dark blocked area means that a similar
harmonic structure sustains for a while. : Block
 Captures homogeneity

17. Self-Similarity Matrix
For example,
Harmony sustains for this long.
Similar harmonic structure appears on
these parts from the entire song.

18. Self-Similarity Matrix
There should dark black diagonal line because chroma value of
every frame is exactly same as itself.

19. Self-Similarity Matrix
If there is a similar pattern of harmonic movement(i.e. same
melody pattern), a dark line appears. : Path
 Captures repetition

20. Self-Similarity Matrix
If a similar harmonic change(movement)
takes place at a different tempo, the
gradient of the path changes.
(The gradient of the path indicates the
relative tempo difference between the
two related segments.)

21. SSM Enhancement : finding suitable feature

22. SSM Enhancement : finding suitable feature
• Length l : used to smooth or average the feature value over l consecutive frames
• Downsampling param d : reduces the feature rate by a factor of d
Ex) Assume that chroma features were extracted with feature rate of 10 Hz.
Applying l = 40  4 seconds of audio (window size)
Applying d = 10  feature rate to be 1 Hz (feature rate)
Cf. Adaptive windowing (based on previously extracted onset and beat position)
 will be covered in Tempo related chapter.

23. SSM Enhancement : finding suitable feature
Various chroma representations and resulting SSMs for the
Hungarian Dance No. 5 by Johannes Brahms.
(a) Usage of original normalized chroma features (10 Hz)
(b) Applying l = 40 and d = 10 (1 Hz) (Applied repectively)
(c) Applying l = 160 and d = 20 (0.5 Hz)
(d) Applying l = 480 and d = 50 (0.2 Hz)

24. SSM Enhancement
• Even though particular segments have identical(or similar)
musical(harmonic) structure, there can be variations in
instrumentation, articulation, or dynamics.
 causing them to have significantly different chroma value sequences
• SSM can be augmented by using longer analysis window. (but it will
smooth out important details)

25. SSM Enhancement : path smoothing
Challenge: Presence of musical variations
 Fragmented paths and gaps
 Paths of poor quality
 Regions of constant (low) cost
 Curved paths
Idea: Enhancement of path structure

26. SSM Enhancement : path smoothing
• Apply image processing technique. : apply an averaging filter(low-
pass filter) in the direction of the main diagonal
 an emphasis of diagonal information and softening of nondiagonal
structures
: averaging the similarity values of two subsequences of length L
(starting from (n, m))
But what if there are relative tempo differences?

27. SSM Enhancement : path smoothing
• Apply a multiple filtering approach, where the SSM is smoothed
along various directions that lie in a neighborhood of the diagonal
direction.
• If the tempo difference between the two segments is given by a real
number θ > 0 (the second segment played θ times slower than the
first one), the resulting gradient is (1,θ)
Ex)
α1 and α2 played at the same tempo.
 gradient (1, 1)
α2 is played at the half tempo.
 gradient (1,2)

28. SSM Enhancement : path smoothing
• Define a (finite) set Θ consisting of tempo parameters θ ∈ Θ for
different relative tempo differences.
• Compute for each such θ a matrix SL,θ and obtain a final matrix SL,Θ
by a cell-wise maximization over all θ ∈ Θ :
* use prior information on the expected relative tempo differences Θ
Θ = {0.66,0.81,1.00,1.22,1.50}
 Filtering along 5 different directions

29. SSM Enhancement : path smoothing
(a) Original SSM using chroma features
(resolution of 2 Hz).
(b) SSM after applying diagonal smoothing.
(c) SSM after applying tempo-invariant
smoothing.
(d) SSM after applying forward–backward
smoothing
 Takes care of fading out problem by
taking cell-wise maximum over forward-
smoothed and backward-smoothed matrices

30. SSM Enhancement : transposition invariant
• Certain musical parts are repeated in a transposed form.
 we want to extract repetitive structure regardless of transposition.
• Use i-transposed self-similarity matrix ρi(S)
• Taking a cell-wise maximum over the twelve different cyclic shifts, we
obtain a single transposition-invariant self-similarity matrix STI:

31. SSM Enhancement : transposition invariant
(a) Original SSM using
chroma features
(resolution of 1 Hz).
(b) Path-enhanced
SSM.
(c) 1-transposed
SSM.
(d) 2-transposed SSM.
(e) Transposition-invariant SSM.

32. SSM Enhancement : transposition invariant
transposition index matrix
: stored the maximizing shift indices in an additional N-square matrix I.

33. SSM Enhancement : thresholding
• We want to reduce unwanted noise
 suppressing all values that fall below a given threshold.
• Use an additional penalty parameter δ ≤ 0, setting all original values
below the threshold to the value δ

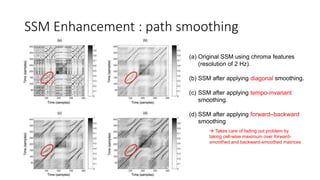
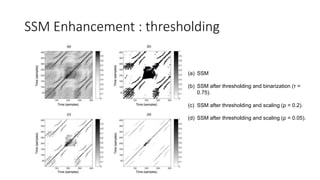
34. SSM Enhancement : thresholding
• Scaling from the range [τ,μ]  [0,1]
( for μ := maxn,m{S(n,m)} > τ, otherwise all entries are set to zero)
• Choose τ in a relative fashion (ρ · 100%)
: keeping ρ · 100% of the cells with the highest values using a relative
threshold parameter ρ ∈ [0,1]
(Local strategy of setting τ in a column- and rowwise fashion)

35. SSM Enhancement : thresholding
(a) SSM
(b) SSM after thresholding and binarization (τ =
0.75).
(c) SSM after thresholding and scaling (ρ = 0.2).
(d) SSM after thresholding and scaling (ρ = 0.05).

36. SSM Enhancement : in summary
(a) SSM (chroma features of 2Hz)
(b) diagonal smoothing. (c) tempo-invariant / forward–backward smoothing.
(d) Transposition-invariant SSM. (e) Transposition index matrix. (f) thresholding w/ penalty and scaling (ρ = 0.2, δ = −2)

37. Audio thumbnailing
• Automatically determining the most representative section, which
may serve as a kind of “preview” giving a listener a first impression of
the song or piece of music
• Identify a section that has on the one hand a certain minimal
duration and on the other many (approximate) repetitions.

38. Audio thumbnailing
Two approaches
1. Path extraction
problem : Paths of poor quality (fragmented, gaps) / Block-like structures / Curved paths
2. Grouping
problem : Noisy relations (missing, distorted, overlapping) / Transitivity computation difficult
 Both steps are problematic!
Main idea: Do both, path extraction and grouping, jointly
- One optimization scheme for both steps
- Stabilizing effect
- Efficient

39. Audio thumbnailing
• a fitness measure : assigns a fitness value to each audio segment.
• two aspects of a fitness measure.
1) indicates how well a given segment explains other related segments
2) indicates how much of the overall music recording is covered by all
these related segments.

40. Audio thumbnailing – fitness measure
• Fitness measure : simultaneously establish all relations between a given segment and its
repetitions.
segment
Induced
segments
paths

41. Audio thumbnailing – fitness measure
• Consider a fixed segment
• A path family over a segment is a family of paths such that the
induced segments do not overlap
Not a path family

42. Audio thumbnailing – fitness measure
• Choosing Optimal path family (for each segment)
the score σ(P) of the path family P an optimal path family of maximal score
(induced segment family)

43. Audio thumbnailing – fitness measure
• Optimizing algorithm : Dynamic programming
1) Given two sequences, say X = (x1,x2,...,xN) and Y = (y1,y2,...,yM),
compute an optimal path that globally aligns X and Y,
where the first elements as well as the last elements of the two sequences are to be aligned.
2) The step size condition as specified by the set Σ constrains the slope of the path.
Ex) Σ = {(2, 1), (1, 2), (1, 1)}
3) Each element of X is aligned to at most one element of Y.
 Find score-maximizing path family .

44. DP in a nutshell..

45. DP in a nutshell..

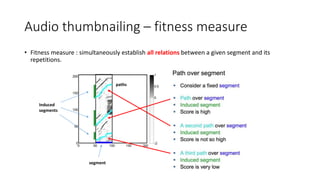
46. Audio thumbnailing – fitness measure
computing an optimal path family over a given segment α = [s : t] ⊆ [1 : N]
1) N × M submatrix Sα (segment α = [s : t] with M := |α|)
columns s : t of the self-similarity matrix S.
2) An accumulated score matrix D ∈ RN,M+1 by a recursive procedure.
(D : [1 : N] rows, [0 : M] columns)
3) Φ (n, m) : a set of predecessors of cell (n, m)
 all cells that may precede (n,m) in a valid path family.
4) Accumulated score matrix :
5) Constraint conditions
: values of D for the remaining index pairs (n, m) with n = 1 or m ∈ {0, 1}
for n∈[2:N]
Complexity: O(MN)

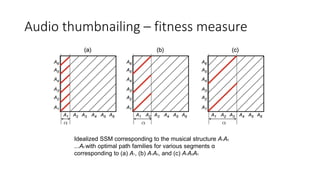
47. Audio thumbnailing – fitness measure
computing an optimal path family over a given segment α = [s : t] ⊆ [1 : N]
Submatrix Sα w/ α = [50 : 100]
Accumulated score matrix D
Optimal path family

48. Audio thumbnailing – fitness measure
• Compute an optimal path family P∗ = {P1,...,PK} for a given segment α  repetition relations of α
1) Simply use the total score σ(P∗) : not good because it not only depends on the lengths of α and the paths, but also
captures trivial self-explanations (each segment α explains itself perfectly, information that is encoded by the main diagonal
of a self-similarity matrix.)
2) subtracting the length |α| from the score σ(P∗) + normalize the score with regard to the lengths Lk := |Pk| of the paths Pk
contained in the optimal path family P∗.
normalized score σ ̄(α)
Intuitively, the value σ ̄(α) expresses the average score of the optimal path family P∗ (minus a proportion for the self-
explanation)
normalization eliminates the influence of segment lengths  how well it explains other segments.

49. Audio thumbnailing – fitness measure
• Besides repetitiveness, another issue is how much of the underlying music recording is covered
by the thumbnail and its related segments.
• To capture this property, we define a coverage measure for a given α.
• To this end, let A∗ := {π1 (P1 ), . . . , π1 (PK )} be the (induced-) segment family induced by the
optimal path family P∗, and let γ(A∗) be its coverage.
• We define the normalized coverage γ ̄(α) :
γ ̄(α)  the ratio between the union of the induced segments of α and the total length of the original recording
(minus a proportion for the self-explanation)

50. Audio thumbnailing – fitness measure
• a high average score and a high coverage : both important
• Shorter segments often have a higher average score, but a lower
coverage, whereas longer segments tend to have a lower average
score, but a higher coverage.  need to balance out.
 fitness φ(α) of the segment α to be the harmonic mean

51. Audio thumbnailing – fitness measure
Idealized SSM corresponding to the musical structure A1A2
...A6 with optimal path families for various segments α
corresponding to (a) A1, (b) A1A2, and (c) A1A2A3

52. Audio thumbnailing – thumbnail selection
• Define the audio thumbnail to be the segment of maximal fitness:
• Add a lower bound θ for the minimal possible thumbnail length
 this segment has nonoverlapping repetitions that cover a possibly
large portion of the audio recording

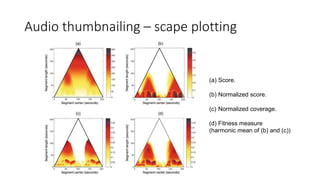
53. Audio thumbnailing – scape plotting
• There are (N + 1)N /2 different segments α = [s : t] ⊆ [1 : N] where s,t ∈ [1 : N]
• Instead of considering start and end points, each segment can also be uniquely described by its center :
scape plot ∆ :

54. Audio thumbnailing – scape plotting
(b) α = α∗ = [68 : 89]
(corresponding to B2)
(c) α = [41 : 67]
(corresponding to B1
)
(d) α = [131 : 150]
(corresponding to A3 )
(e) α = [21 : 89]
(corresponding to A1B1B2)
the thumbnail segments of maximal fitness
(Choose maximum point)
c(α) = 78.5
|α| = 22

55. Audio thumbnailing – scape plotting
α = α∗ = [68 : 89]
(corresponding to
B2)
α = [41 : 67]
(corresponding to B1 )
Recall that the introduced fitness measure slightly favors shorter segments
 recording the B2-part is played faster than the B1-part, the fitness measure favors the B2-part
segment over the B1-part segment.
vs

56. Audio thumbnailing – scape plotting
(a) Score.
(b) Normalized score.
(c) Normalized coverage.
(d) Fitness measure
(harmonic mean of (b) and (c))

57. Audio thumbnailing – scape plotting
Beatles song “Twist and Shout.”
The song contains a short harmonic phrase, a so-
called riff, which is repeated over and over again.
α∗ = [127 : 130] is very short and leads to a large
number of spurious induced segments.

58. Novelty-Based Segmentation
• Segment boundaries are often accompanied by a change in
instrumentation, dynamics, harmony, tempo, or some other
characteristics.
• Often a homogeneous segment is followed by another homogeneous
segment that stands in contrast to the previous one
 locate points in time where such musical changes occur, thus
marking the transition between two subsequent structural parts

59. Novelty-Based Segmentation
• One idea in novelty detection is to identify the boundary between two
homogeneous but contrasting segments by correlating a checkerboard-like
kernel function along the main diagonal of the SSM. : novelty function.
• Ex. correlating S with a kernel that itself looks like a checkerboard
‘difference between a “coherence” and an “anti-coherence”’ kernel
measures the self-similarity on either side of the
center point and will be high when each of the
two regions is homogeneous
measures the cross-similarity between the
two regions and will be high when there is
little difference across the center point

60. Kernel/convolution
Kernel (image processing)
: In image processing, a kernel, convolution matrix, or mask is a small matrix. It is useful for blurring, sharpening, embossing, edge detection,
and more. This is accomplished by means of convolution between a kernel and an image.
https://en.wikipedia.org/wiki/Kernel_(image_processing)
Gabor filter
사람의 시각체계가
반응하는 것과 비슷.
외곽선을 검출.

61. Novelty-Based Segmentation
• Since in this book we adopt a centered view (where a physical time position is
associated to the center of a window or kernel), we assume that the size of the
kernel is odd given by M = 2L + 1 for some L ∈ N.
If L = 2,
The zero row and the zero column in the middle have been
introduced more for theoretical reasons to ensure the symmetry of
the kernel matrix.

62. Novelty-Based Segmentation
• The checkerboard kernel can be smoothed to avoid edge effects using windows
that taper towards zero at the edges. For this purpose, one may use a radially
symmetric Gaussian function φ : R2 → R defined by :
(ε > 0 allows for adjusting the degree of tapering)
• To compensate for the influence of the actual kernel size and of the tapering, one
may normalize the kernel.

63. Novelty-Based Segmentation
Checkerboard kernel functions of size M = 21 (L = 10).
(a,b) Box-like checkerboard kernel and 3D plot.
(c,d) Gaussian checkerboard kernel and 3D plot.

64. Novelty-Based Segmentation
• Slide a suit- able checkerboard kernel K along the main diagonal of
the SSM and sum up the element-wise product of K and S:

65. Novelty-Based Segmentation
Dependency of novelty functions on
characteristics of the feature representation
and the kernel size.
(a) SSM using tempo-based features.
(b–d) Novelty functions derived from (a)
using a kernel of small/medium/large size.
(e) SSM using chroma-based features.
(f–h) Novelty functions derived from (e)
using a kernel of small/medium/large size.

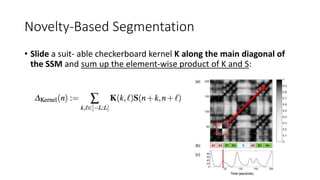
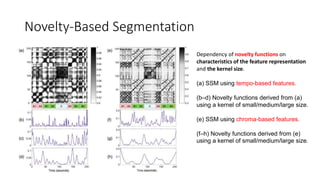
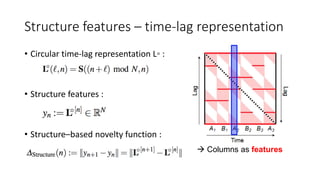
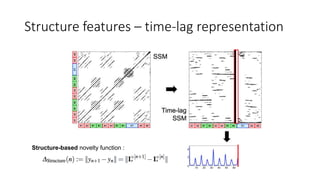
66. Structure features – time-lag representation
• time-lag representation of S :
(for n∈[0:N−1] and l∈[−n:N−1−n])
Lines that are parallel to the main diagonal in S
become horizontal lines in L.

67. Structure features – time-lag representation
• Circular time-lag representation L◦ :
• Structure features :
• Structure–based novelty function :
 Columns as features

68. Structure features – time-lag representation
Structure-based novelty function :

69. Evaluation
• Compare an estimated result obtained by some automated
procedure against some reference result.(ground truth)

70. Evaluation – part labeling
Pairwise precision, recall, and F-measure.
(a) Positive items (indicated by gray boxes) with regard to the reference
annotation.
(b) Positive items (indicated by gray boxes) with regard to the estimated
annotation.
(c) True positive (TP), false positive (FP), and false negative (FN) items.

71. Evaluation – boundary annotation
(a) Reference boundary annotation.
(b) Estimated boundary annotation.
(c) Evaluation of (b) with regard to (a).
(d) τ-Neighborhood of (a) using the tolerance parameter τ = 1.
(e) Evaluation of (b) with regard to (d).
(f) τ -Neighborhood of (a) using the tolerance parameter τ = 2.
(g) Evaluation of (b) with regard to (f).

72. Evaluation – thumbnail detection
Typical error sources in thumb-nailing and
music structure analysis
(a) Confusion problem for Beatles song “Martha
My Dear.”
(b) Substructure (oversegmentation) problem
for Beatles song “While My Guitar Gently
Weeps.”
(c) Superordinate structure
(undersegmentation) problem for Beatles
song “For No One.”