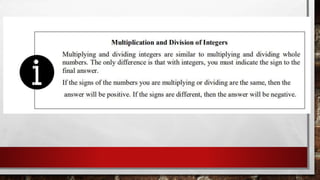
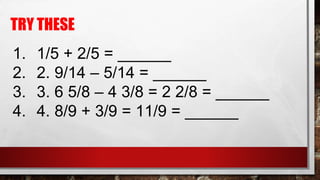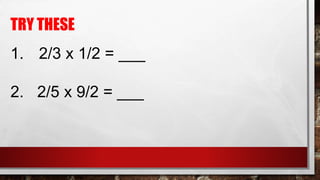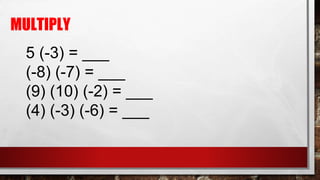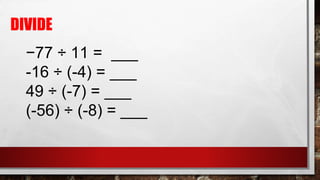The document is a lesson on fractions and decimals that explains various types of fractions, such as proper, improper, unit, and mixed fractions, including their definitions and examples. It also covers converting fractions to decimals and percentages, operations with fractions, including addition, subtraction, multiplication, and division, and provides sample problems for practice. The lesson emphasizes finding common denominators for unlike fractions and outlines methods for each mathematical operation.

1. Fractions and Decimals
LESSON 1

2. Parts of a Fraction
Denominator - indicates how many parts the whole has
been divided into. It is placed in the lower part of the
fraction.
Numerator- indicates how many sections of the fraction are
represented. It is placed in the upper part of the whole.

3. Types of Fractions:
• Proper Fraction – is a fraction in which the numerator is less than its
denominator. It is often smaller than the whole. Example: 5/7, 3/8, 2/5, etc.
• Improper Fraction - is the type of fraction in which the numerator is more
than or equal to its denominator. It is always the same or greater than the
whole. Example: 4/3, 5/2, 8/5, etc.
• Unit Fraction – is a fraction with 1 as numerator. Example: 1/4, 1/7, 1/9, etc.
Mixed Fraction - is a mixture of a whole and a proper fraction. Example: 5
1/3; 2 2/5, etc.
• Like Fractions - (similar) are the fractions that have the same denominators.
Example: 5/15, 3/15, and 17/15.
• Unlike fractions - (dissimilar) are the fractions which have different
denominators. Example: 2/7, 9/11 and 3/13.

4. Types of Fractions:
• Proper Fraction – is a fraction in which the numerator is less than its
denominator. It is often smaller than the whole. Example: 5/7, 3/8, 2/5, etc.
• Improper Fraction - is the type of fraction in which the numerator is more
than or equal to its denominator. It is always the same or greater than the
whole. Example: 4/3, 5/2, 8/5, etc.
• Unit Fraction – is a fraction with 1 as numerator. Example: 1/4, 1/7, 1/9, etc.
Mixed Fraction - is a mixture of a whole and a proper fraction. Example: 5
1/3; 2 2/5, etc.
• Like Fractions - (similar) are the fractions that have the same denominators.
Example: 5/15, 3/15, and 17/15.
• Unlike fractions - (dissimilar) are the fractions which have different
denominators. Example: 2/7, 9/11 and 3/13.

5. Converting fractions to decimals and percent
To convert fractions to decimals, divide the numerator by
the denominator. The result is the decimal form. To express
the decimal form to percent, move the decimal point two
places to the right and affix the percent symbol.
Example: 4/5
4 ÷ 5 = 0.8 decimal form;
0.8 = 80% percent form
- 4/5 = 0.8 = 80%

6. Converting percent to decimals and fractions
Write the percent as a fraction with a denominator of 100
and simplify. That’s the fraction
form. For the decimal form, just drop the percent symbol
and move the point 2 places to the
left.
Example: 88%
88% = 88/100 = 22/25 fraction form;
0.88 decimal form
- 88% = 22/25 = 0.88

7. Converting decimals to fractions and percent
To convert decimal to percent, just move the
point two places to the right and affix the
percent symbol.
Example: 0.25 = 25%

8. Converting decimals to fractions and percent
To convert decimal to fraction, rewrite the number by ignoring the
decimal point. Divide the number by the power of 10 such that the
number of zeros in that should be equal to the number of decimal
places in the given number. Simplify the fraction.
Examples: 0.25 = 25/100 = ¼
6.5 = 65/10 = 13/2

9. Adding and Subtracting Fractions with Like
Denominators
Add or subtract the numerators of the given
fractions and retain the same
denominator.Simplify (reduce) the fraction, if
possible.

10. TRY THESE
1. 1/5 + 2/5 = ______
2. 2. 9/14 – 5/14 = ______
3. 3. 6 5/8 – 4 3/8 = 2 2/8 = ______
4. 4. 8/9 + 3/9 = 11/9 = ______

11. Adding and Subtracting Fractions with Unlike
Denominators
Follow the steps:
1. Find the LCD of the fractions.
2. Rename the fractions using the LCD.
3. Add or subtract the numerators.
Denominator remains.
4. 4. Simplify, if necessary.

12. TRY THESE
1. Add the fractions 1/5 and 1/3
2. Subtract the fractions 7/9 and 2/3.
3. Subtract: 17 5/9 – 11 5/12

13. Multiplying Fractions
- To multiply two (or more) fractions, multiply across,
numerator by numerator and denominator by
denominator. Simplify the answer, if possible.
- When multiplying fractions, we can simplify the
fractions and also simplify diagonally. This isn’t
necessary, but it can make the numbers smaller and
keep you from simplifying at the end.

14. TRY THESE
1. 2/3 x 1/2 = ___
2. 2/5 x 9/2 = ___

15. Dividing Fractions
To divide two fractions, change the
operation to multiplication and take the
reciprocal of the second fraction (flip the
second fraction). Keep-Change-Change.

16. TRY THESE
1. 2/5 ÷ 9/2 = ___
2. 2 1/3 ÷ 3 2/3 = ___

17. 6 – 8 = -2
Change the sign of the subtrahend by its opposite, and then proceed
to addition.
6 + (-8)
6 + (-8)= -2 Adding unlike signs

18. TRY THESE:
14 – (-13) = ___
-12 – 11 = ___
-15 – (-10) = ___
-16 – (-26) = ___

20. MULTIPLY
5 (-3) = ___
(-8) (-7) = ___
(9) (10) (-2) = ___
(4) (-3) (-6) = ___

21. DIVIDE
−77 ÷ 11 = ___
-16 ÷ (-4) = ___
49 ÷ (-7) = ___
(-56) ÷ (-8) = ___