The document provides an overview of informed search algorithms, highlighting the role of heuristics in enhancing search efficiency by utilizing information about the goal state. It discusses the benefits of informed searches over blind searches, including improved pattern recognition, decision-making, and navigating complex problem spaces. It also details specific algorithms like best-first and A* search, and outlines their methodologies, advantages, and applications.

1. 1
Informed Search Algorithms

2. Informed Search Algorithms
2
 The algorithms have information on the goal state, which helps
in more efficient searching.
 This information is obtained by something called a heuristic
Search.
 Informed search algorithm contains an array of knowledge such
as how far we are from the goal, path cost, how to reach to goal
node, etc.
 This knowledge help agents to explore less to the search space
and find more efficiently the goal node.
 The informed search algorithm is more useful for large search
space.

3. 3
 What is the Need for Informed Search?
 Here are some of the primary reasons why an informed search is essential:
 Domain Knowledge: Heuristics are a type of domain-specific knowledge that may be
used in informed search algorithms. With this information, the search process can be
directed in ways that are not possible with blind search techniques. For example, a
heuristic based on real-time traffic information can help avoid busy routes while
planning a trip.
 Pattern Recognition: In order to find patterns or characteristics in data more
effectively, informed search can be utilized in pattern recognition tasks. Heuristic-
guided search, for example, can enhance model training and feature selection in
machine learning.
 Efficiency: In general, informed search algorithms beat blind (uninformed) search
algorithms in terms of efficiency. They may reduce the search space and frequently find
solutions more rapidly by making well-informed selections about which paths to look
at first using heuristic knowledge. This effectiveness is crucial in general, complicated
problem fields.
 Complex Decision Making: Applications that require complicated decision-making
processes, such as playing games (like chess or go), are helped by informed search.
Machine learning robots can analyze future moves and strategies more effectively with
the use of heuristic knowledge.
 Problem Complexity: Many issues in the real world have large search areas and are
very difficult. AI systems can more successfully navigate these complex topographies
by concentrating on the most promising areas. Blind search algorithms might have
trouble finding answers in an appropriate amount of time without heuristics.

4. 4
 Types of Informed Search in Artificial Intelligence
 Heuristic Function
 Best First Search
 A* Search
 Hill Climbing

5. Heuristic Function
5
 A heuristic function is a strategy for solving problems by determining
the cost or distance to a goal state in a search problem by making a
“best guess” or using a rule of thumb. A search algorithm can be
directed in the right direction by using the heuristic function, which
calculates how far the objective state is from the present state.
 These features are used by intelligent search engines as an extra
source of data to decide which course to take. Heuristic functions are
crucial in informed search algorithms for this reason.
 Example:
 A player can begin the game of tic tac toe from a variety of
positions, and each position has a different chance of winning. The
first player, however, has the best chance of succeeding if they
begin from the middle of the board. As a result, winning chances
can be used as a heuristic.

6. 6
 It takes the current state of the agent as its input and produces
the estimation of how close agent is from the goal.
 The heuristic method, however, might not always give the
best solution, but it guaranteed to find a good solution in
reasonable time.
 Heuristic function estimates how close a state is to the goal.
 It is represented by h(n), and it calculates the cost of an
optimal path between the pair of states.
 The value of the heuristic function is always positive.
 Admissibility of the heuristic function is given as:
h(n) <= h*(n)
 Here h(n) is heuristic cost, and h*(n) is the estimated cost

7. Pure Heuristic Search
7
 Pure heuristic search is the simplest form of heuristic search
algorithms.
 It expands nodes based on their heuristic value h(n). It maintains
two lists, OPEN and CLOSED list.
 In the CLOSED list, it places those nodes which have already
expanded and in the OPEN list, it places nodes which have yet not
been expanded.
 On each iteration, each node n with the lowest heuristic value is
expanded and generates all its successors and n is placed to the
closed list.
 The algorithm continues unit a goal state is found.
 In the informed search we will discuss two main algorithms which
are given below:
 Best First Search Algorithm(Greedy search)
 A* Search Algorithm

8. Best First Search Algorithm
8
 Greedy best-first search algorithm always selects the path which
appears best at that moment.
 It is the combination of depth-first search and breadth-first search
algorithms.
 It uses the heuristic function and search.
 Best-first search allows us to take the advantages of both algorithms.
 With the help of best-first search, at each step, we can choose the
most promising node.
 In the best first search algorithm, we expand the node which is
closest to the goal node and the closest cost is estimated by heuristic
function, i.e.
f(n)= g(n)
 Were, h(n)= estimated cost from node n to the goal.
 The greedy best first algorithm is implemented by the priority
queue.

9. Best first search algorithm
9
 Step 1: Place the starting node into the OPEN list.
 Step 2: If the OPEN list is empty, Stop and return failure.
 Step 3: Remove the node n, from the OPEN list which has the
lowest value of h(n), and places it in the CLOSED list.
 Step 4: Expand the node n, and generate the successors of node n.
 Step 5: Check each successor of node n, and find whether any
node is a goal node or not. If any successor node is goal node,
then return success and terminate the search, else proceed to Step
6.
 Step 6: For each successor node, algorithm checks for evaluation
function f(n), and then check if the node has been in either OPEN
or CLOSED list. If the node has not been in both list, then add it
to the OPEN list.
 Step 7: Return to Step 2.

10. Example
10
 Consider the following graph and perform the Best First
Search.

11. 11
 First we have to create two list (data structure) Open and closed and
add the initial node into open list.
 Add the start node into the open list with the heuristic value and then
put the A into the closed list, because the lowest heuristic value of node
is A is only.
 Next expand the A with their intermediate successor and add the
successor node into open list and remove the A from the open list.
 Next arrange the open list in ascending order of their heuristic value
and find the best node (lowest heuristic value).
Open Closed
Node H(n) Node Parent
A 40 A
Open Closed
Node H(n) Node Parent
B 32 A
C 25
D 35

12. 12
 Next find the best successor node and add that node into the
closed list and remove from the open list.
 Next add the successor node of C into the open list and arrange
into the ascending order of their heuristic value.
 Final the best successor and add that node into the closed list and
remove from the open list.
Open Closed
Node H(n) Node Parent
B 32 A
D 35 C A
E 19
F 17
Open Closed
Node H(n) Node Parent
B 32 A
C 25
D 35
Open Closed
Node H(n) Node Parent
F 17 A
E 19 C A
B 32 F C
D 35

13. 13
 Here F is not a goal node, so
Next add to the successor of
F into open list and re-arrange
The node into descending order
Of their heuristic value.
 Next find the best node and add them into the closed list and
delete from the open list.
 Here best node is G that is also a goal node, so we need to
stop the iteration.
 The path we will follow is A->C->F->G .
Open Closed
Node H(n) Node Parent
E 19 A
B 32 C A
D 35 F C
G 0
Open Closed
Node H(n) Node Parent
G 0 A
E 19 C A
B 32 F C
D 35 G F

14. 14

15. Example
15
 Consider the below search problem, and we will traverse it
using greedy best-first search. At each iteration, each node is
expanded using evaluation function f(n)=h(n) , which is given
in the below table.

16. 16
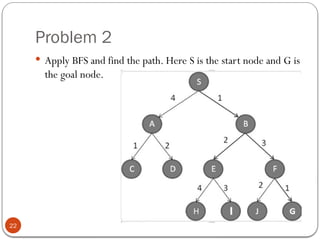
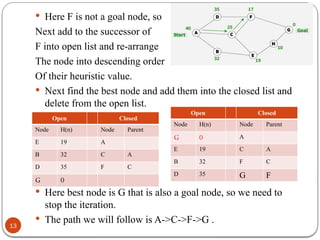
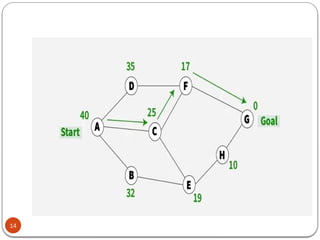
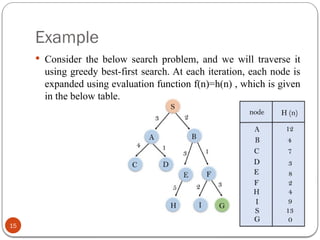
 Expand the nodes of S and put in the CLOSED list
 Initialization: Open [A, B], Closed [S]
 Iteration 1: Open [A], Closed [S, B]
 Iteration 2: Open [E, F, A], Closed [S, B]
Open [E, A], Closed [S, B, F]
 Iteration 3: Open [I, G, E, A], Closed [S, B, F]
Open [I, E, A], Closed [S, B, F, G]
 Hence the final solution path will be:
S----> B----->F----> G

17. 17
 Advantages of Greedy Best-First Search:
 Simple and Easy to Implement: Greedy Best-First Search is a
relatively straightforward algorithm, making it easy to implement.
 Fast and Efficient: Greedy Best-First Search is a very fast
algorithm, making it ideal for applications where speed is
essential.
 Low Memory Requirements: Greedy Best-First Search requires
only a small amount of memory, making it suitable for
applications with limited memory.
 Flexible: Greedy Best-First Search can be adapted to different
types of problems and can be easily extended to more complex
problems.
 Efficiency: If the heuristic function used in Greedy Best-First
Search is good to estimate, how close a node is to the solution, this
algorithm can be a very efficient and find a solution quickly, even
in large search spaces.

18. 18
 Disadvantages of Best-First Search:
 Inaccurate Results: Best-First Search is not always guaranteed
to find the optimal solution, as it is only concerned with finding
the most promising path.
 Local Optima: Best-First Search can get stuck in local optima,
meaning that the path chosen may not be the best possible path.
 Heuristic Function: Best-First Search requires a heuristic
function in order to work, which adds complexity to the
algorithm.
 Lack of Completeness: Best-First Search is not a complete
algorithm, meaning it may not always find a solution if one is
exists. This can happen if the algorithm gets stuck in a cycle or
if the search space is a too much complex.

19. Performance measure
19
 Time Complexity: The worst-case time complexity of
Greedy best first search is O(bm
).
 Space Complexity: The worst-case space complexity of
Greedy best first search is O(bm). Where, m is the maximum
depth of the search space.
 Complete: Greedy best-first search is also incomplete, even if
the given state space is finite.
 Optimal: Greedy best first search algorithm is not optimal.

20. 20
 Applications of Greedy Best-First Search:
 Pathfinding: Greedy Best-First Search is used to find the shortest
path between two points in a graph. It is used in many applications
such as video games, robotics, and navigation systems.
 Machine Learning: Greedy Best-First Search can be used in
machine learning algorithms to find the most promising path
through a search space.
 Optimization: Greedy Best-First Search can be used to optimize the
parameters of a system in order to achieve the desired result.
 Game AI: Greedy Best-First Search can be used in game AI to
evaluate potential moves and chose the best one.
 Navigation: Greedy Best-First Search can be use to navigate to find
the shortest path between two locations.
 Natural Language Processing: Greedy Best-First Search can be
use in natural language processing tasks such as language translation
or speech recognition to generate the most likely sequence of words.
 Image Processing: Greedy Best-First Search can be use in image
processing to segment image into regions of interest.

21. Problem 1
21
 Apply BFS and find the path. Here S is start and E is the goal.

22. Problem 2
22
 Apply BFS and find the path. Here S is the start node and G is
the goal node.

23. Problem 3
23
 Apply BFS and find the path. Here P is the start node and S is
the goal node.