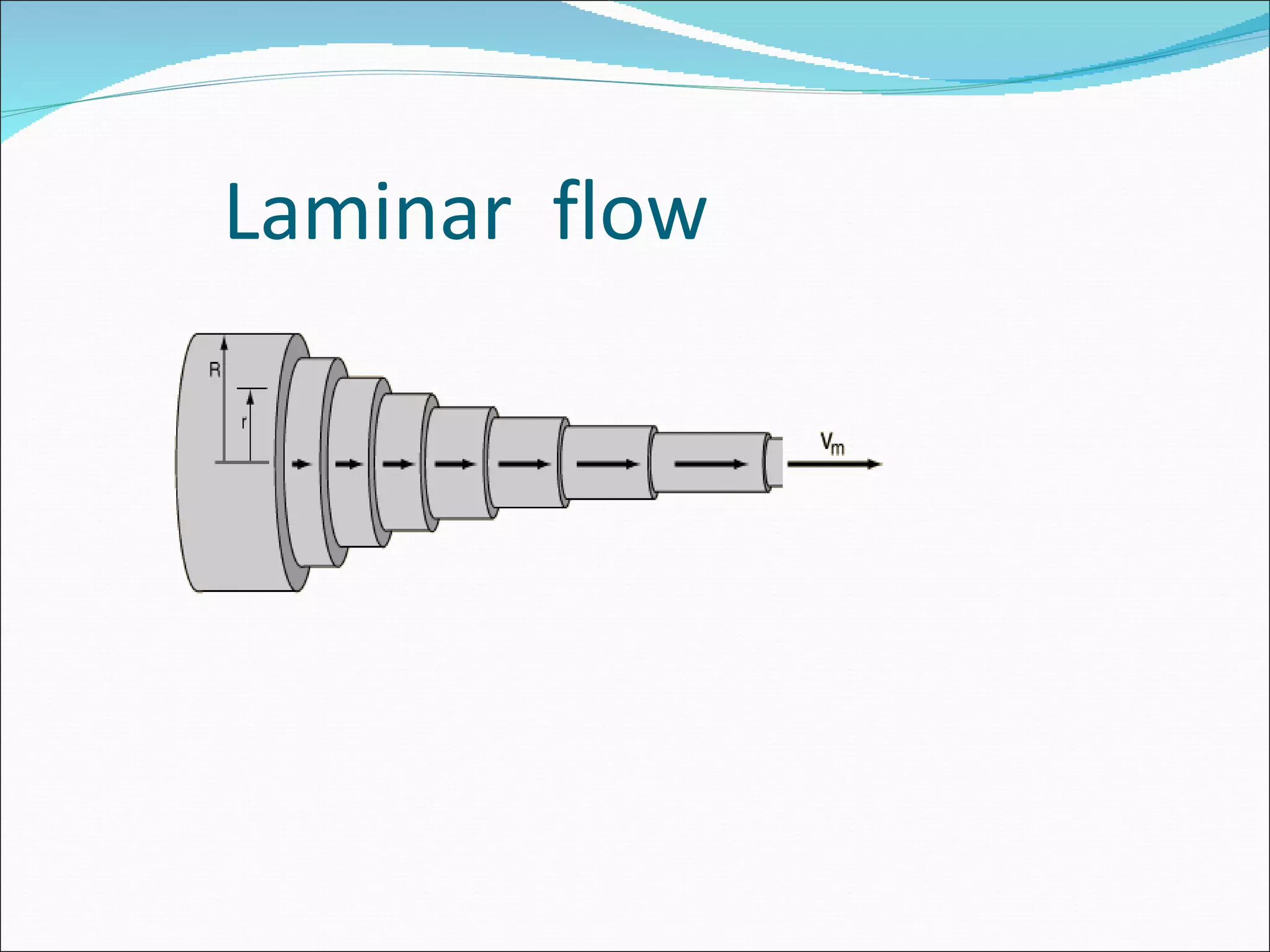
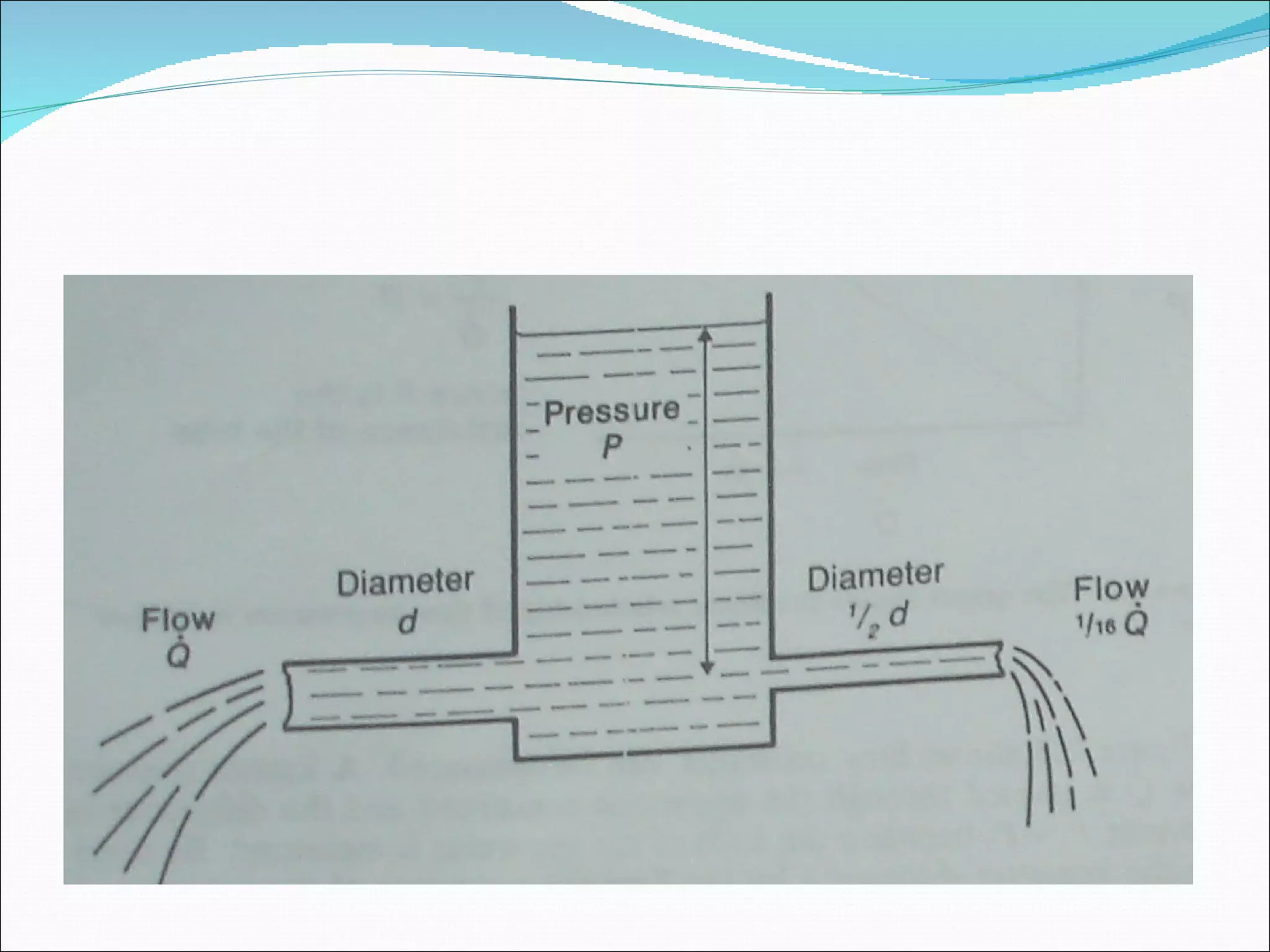
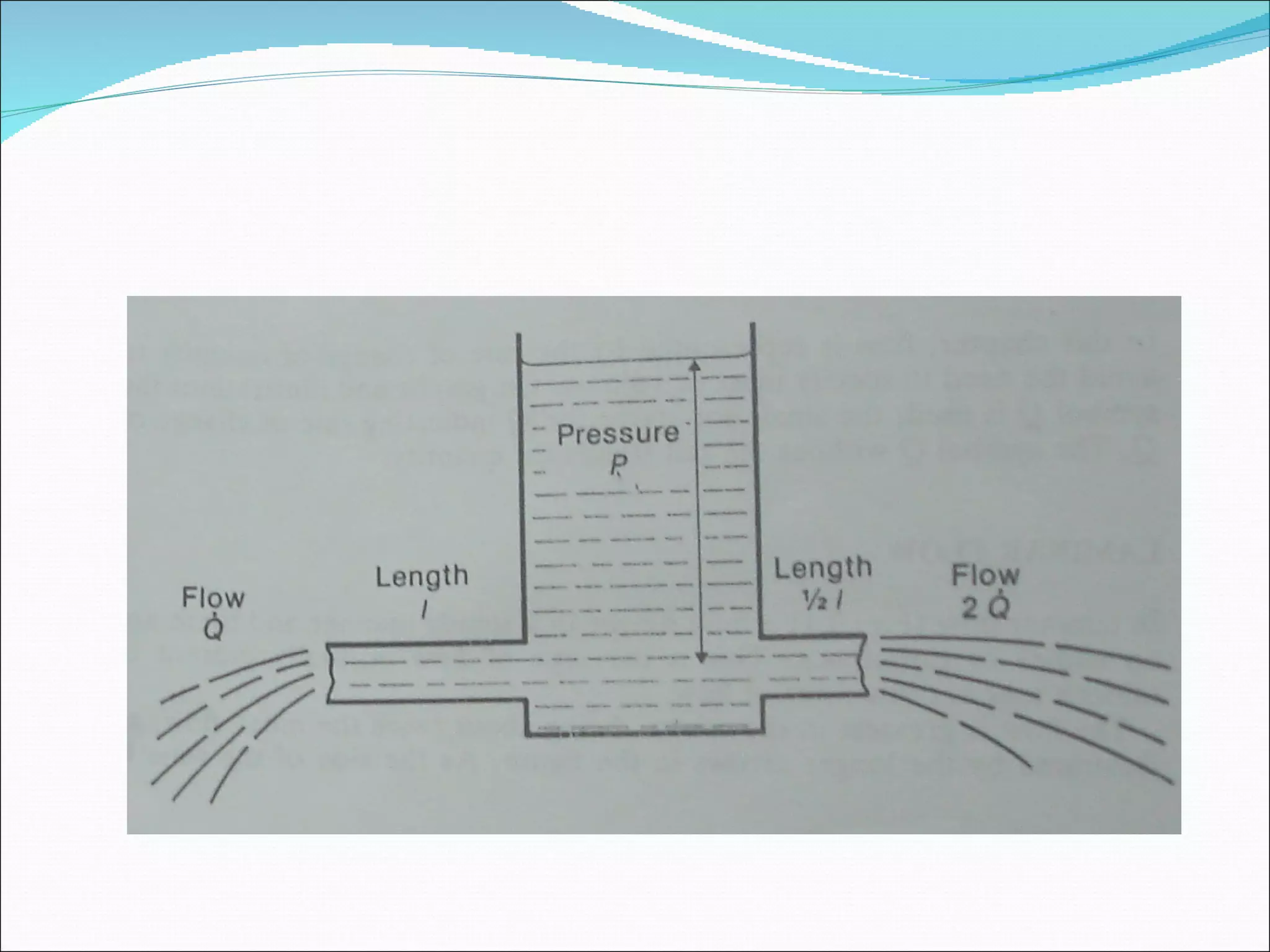
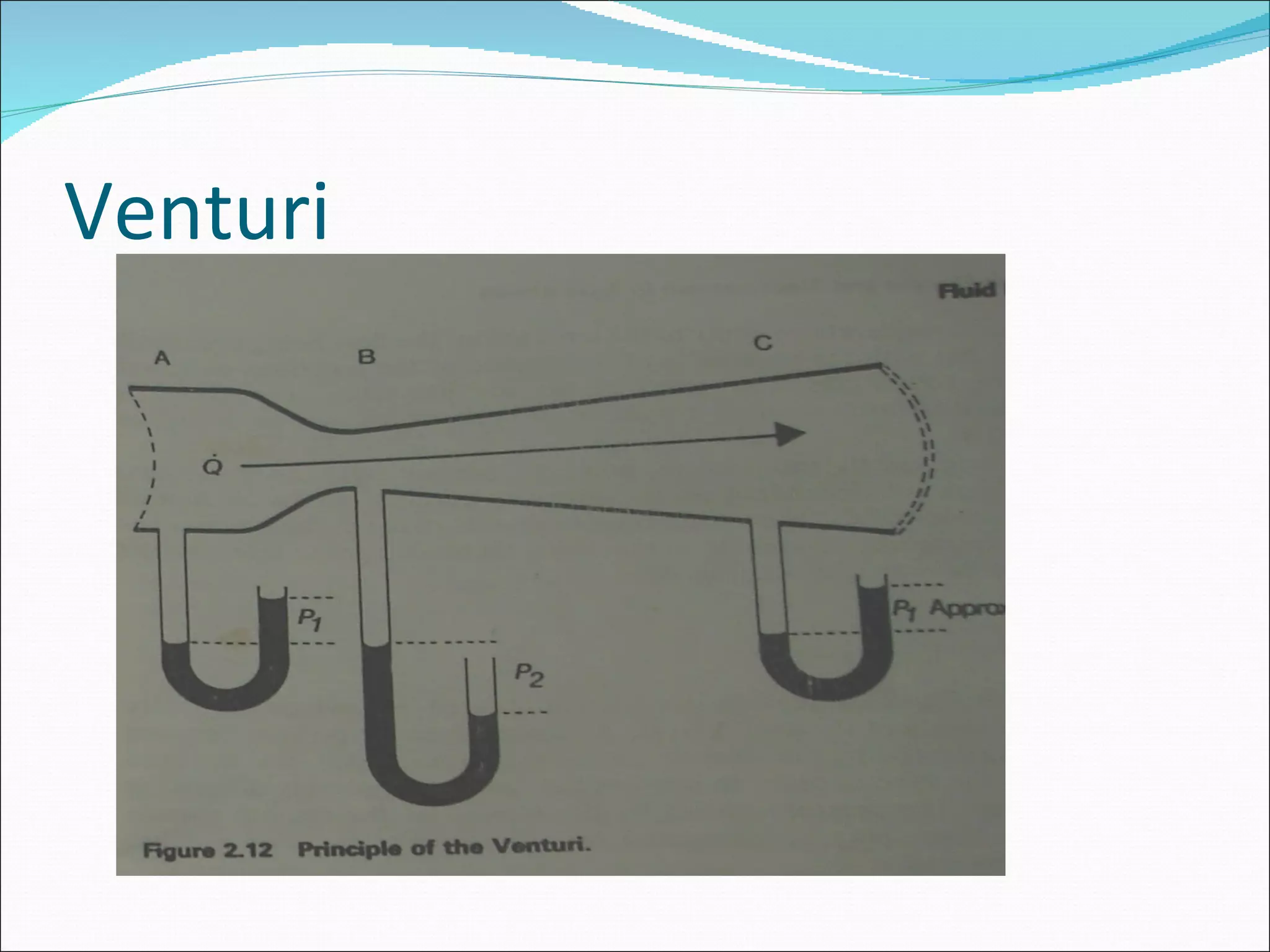
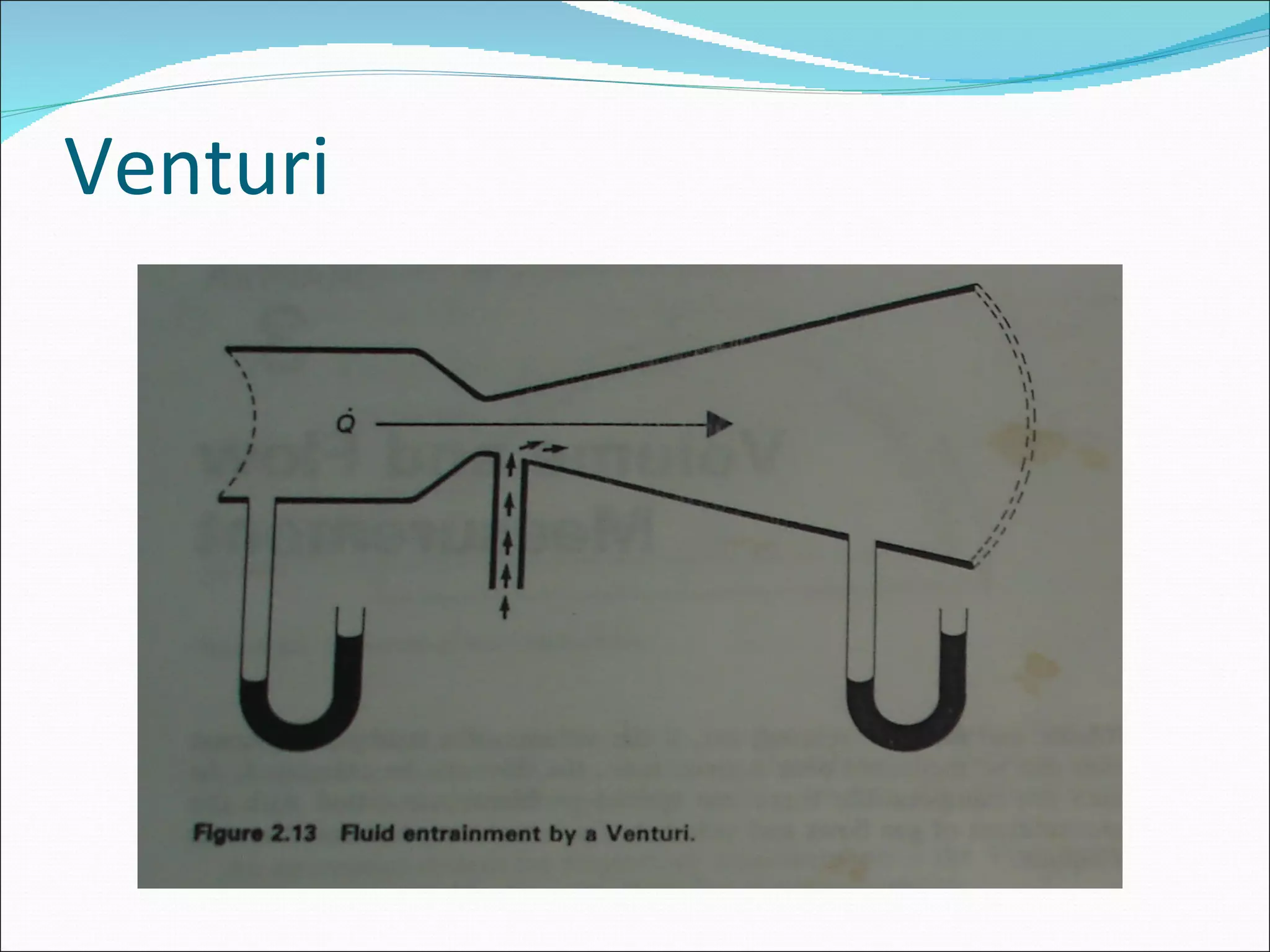
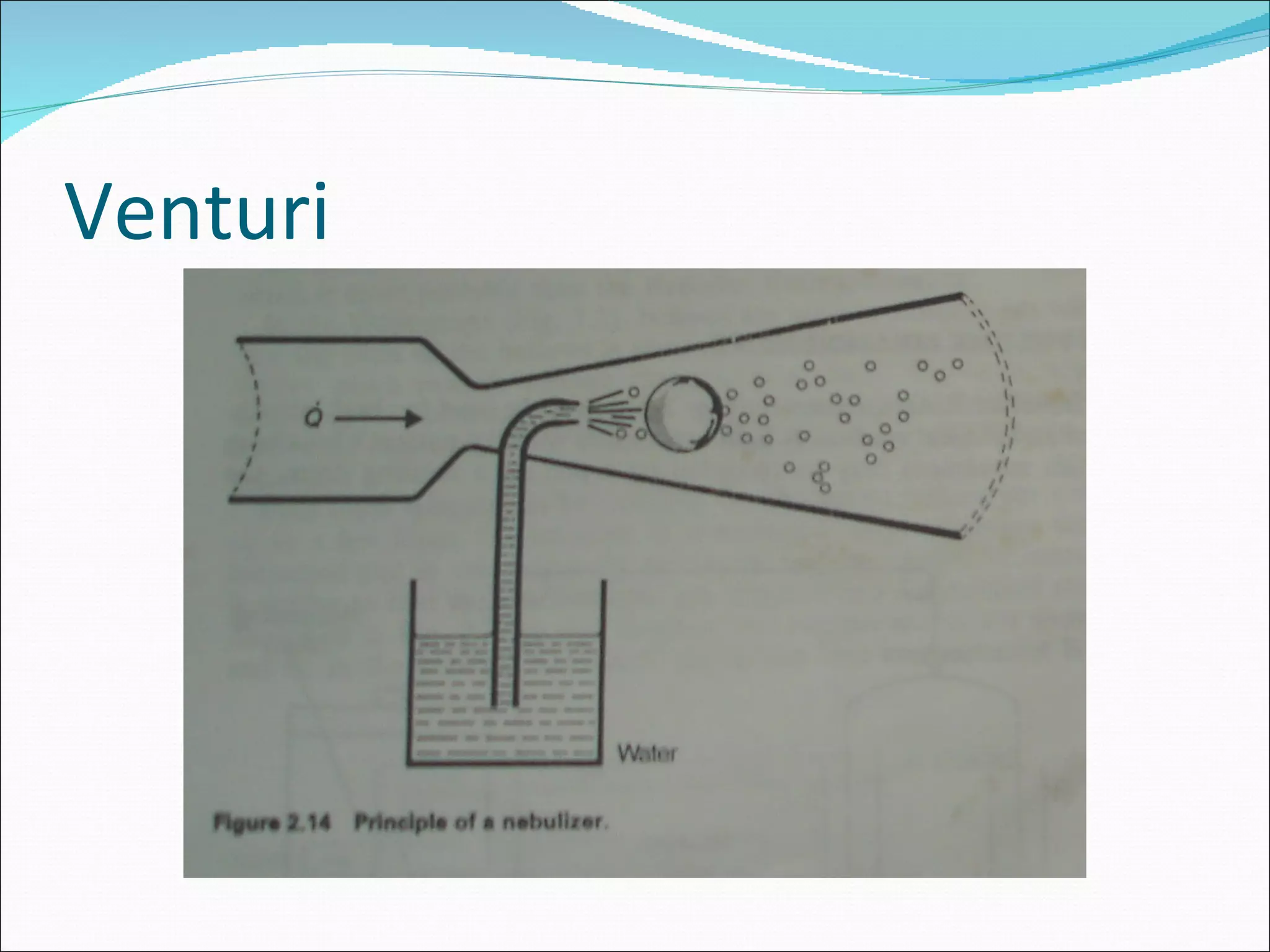
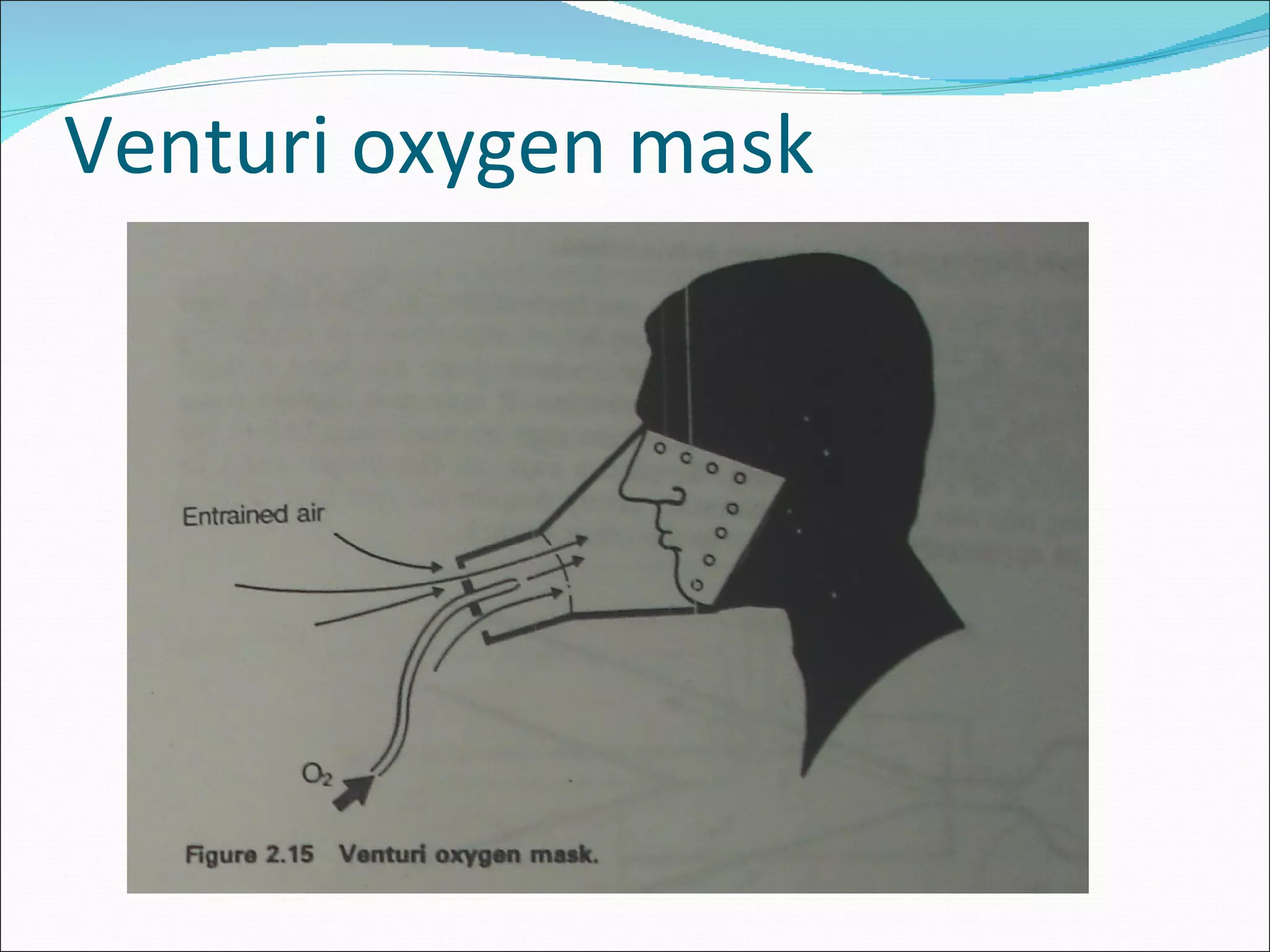
This document discusses different types of fluid flow including laminar, turbulent, and transitional flow. It defines these terms and describes their characteristics. Laminar flow occurs at low velocities and involves fluid particles moving in straight lines. Turbulent flow occurs at higher velocities and involves irregular particle paths. Transitional flow occurs between laminar and turbulent. The document also discusses factors that influence flow such as pressure, tube diameter, viscosity, and Reynolds number. It provides examples of different flow types in medical applications such as respiration and the circulatory system.

1. Dr. Shraddha Naik

2.  Flow is defined as the quantity of a fluid i.e. a gas
or liquid passing in unit time
F=Q/t
F=flow
Q= quantity of liquid
T=time

3. Flow is of three types:
 Laminar flow
 Transitional flow
 Turbulent flow

4. Laminar Flow
 A fluid flows in a steady manner
 No eddies or turbulence
 Present in smooth tubes
 Velocity is low
 Flow is greatest at centre ( 2x mean flow)
 To draw the fluid , a pressure difference must be
present across the ends of tube.

5. Laminar flow
 Laminar flow
 Reynold’s number< 2000
 'low' velocity
 Fluid particles move in straight lines
 Simple mathematical analysis possible

6. Laminar flow

7. Laminar flow

8. Determinants of laminar flow
 Pressure across tube
 Diameter of tube
 length of tube
 Viscosity of tube

9. All these factors are incorporated in an equation
and known as the Hagen- Poiseuille equation


10. Viscosity
 Viscosity of fluid also affects the flow of fluid
 viscosity increase in following condition
- policythemia
-Increased fibrinogen level
- hypothermia
- cigarette smoking
- Age
 Increased viscosity leads to increase risk of
vascular occlusion .

13. Anaesthetic implication
 During fluid resuscitation, a short wide bore cannula
e.g.14G is superior to a 20G cannula or a central line.
 Intubating patients with very small tube increases
resistance to flow and thus pressure increases to
deliver the same amount of flow through the tube.

15. Critical velocity
 This is the velocity for a given fluid for a given tube
beyond which laminar flow gets converted into
turbulent flow.
 When velocity of fluid exceeds this critical velocity ,
the character of flow changes from laminar to
turbulent.
 This critical velocity applies only for a given fluid in a
given tube.

16. Turbulent flow
 Reynolds's number > 4000
 'high' velocity
 Particle paths completely irregular
 Average motion is in the direction of the flow
 Cannot be seen by the naked eye
 Changes/fluctuations are very difficult to detect.
Must use laser.
 Mathematical analysis very difficult - so
experimental measures are used
 Most common type of flow.

17. Onset of turbulent flow
 Turbulent flow occurs –
2. Sharp increase of flow
3. Increase in viscosity or density of the fluid
4. Decrease in diameter of tube

18. Turbulent flow
 Laminar flow change to turbulent flow if constriction
is reached
 Velocity of fluid increases
 Fluid is no longer in a smooth fashion
 Swirls in eddies
 Resistance is higher than for the same laminar flow .
 Flow is no longer directly proportional to pressure

19. Turbulent flow

20. Where turbulent flow is seen ?
 Turbulent flow is present where there is an orifice, a
sharp bend and some irregulararity which may lead to
local increase in velocity

21. Factors affecting flow and pressure during
turbulent flow
 Q α √P
α 1/√ l
α 1/ √ρ
Q= flow
P = Pressure
l = length of tube
ρ = density of fluid

22. All these factors are combined to an index
known as Reynolds number
 Reynold number = vρ∂ / ŋ
v= linear velocity of fluid
ρ = Density
η =viscosity
d = diameter of tube

23. Transitional flow
 Transitional flow
 Reynolds's number-2000-4000
 'medium' velocity

24. Clinical Aspects Of Flow
 Laminar flow is present in bronchi, smaller air
passage as they are narrower than trachea.
 Turbulent flow is present in corrugated rubber
tubing .
 Sharp bend or angles increase turbulence
 In quiet breathing , the flow in resp tract is
laminar, while speaking , coughing or taking deep
breath turbulent flow tends to occur .
 A lining layer of mucus may affect the flow .
 In circulatory system, bruit and murmur can be
heard due to turbulence of flow.

25. Variable orifice flowmeter
 In a variable orifice flow meter there is mixture of
turbulent and laminar flow and for calibration
purposes both viscosity and density is important.
 At low flows, gas flow depends on the viscosity of the
gas.
 At higher flows, gas flow depends on the viscosity of
the gas.
 Recallibration is required if flow meter is used for a
different fluid than for what it was initially desigened.

26. How to measure the resistance
 A constant flow is passed through the apparatus
 Difference in pressure P1-P2 between the ends of
tube is measured
 By dividing pressure difference by flow
 Provided the flow is laminar , resistance is
independent of flow

27. Resistance
Resistance= Pressure / Flow
R= P/ Q

28. How to measure the resistance?

29. Bernoulli’s Principle
 Describes the relationship between the velocity and
pressure exerted by a moving liquid.
 Applied to both liquids as well as gases.
 Venturi effect is based on the Bernoulli’s principle.
 Venturi effect is entrainment of fluid (gas or liquid )
due to the drop in pressure
 When a fluid flows through a constriction in the tube
there is reduction in fluid pressure.
 The fluid velocity correspondingly increases in order
to satisfy the law of conservation of energy.

30. Applications of Venturi effect
 Venturi masks used for oxygen therapy.
 Sander’s jet injector.
 Nebulisation chambers.
 Atomizers that disperse perfumes or spray paints.
 Water aspirators.
 Foam fire fighting nozzles and extinguishers.
 Modern vaporizers.
 Sand blasters to mix air and sand.
 Vehicle carburetors.

31. Venturi

32. Venturi

33. Venturi

34. Venturi oxygen mask