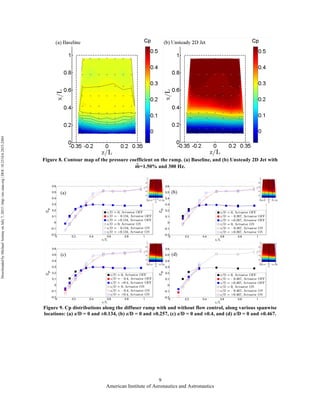
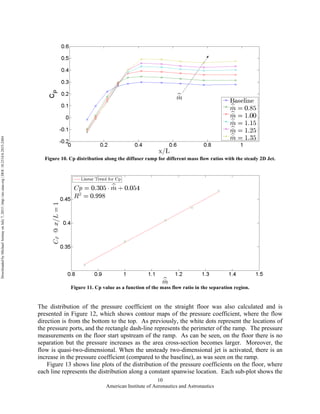
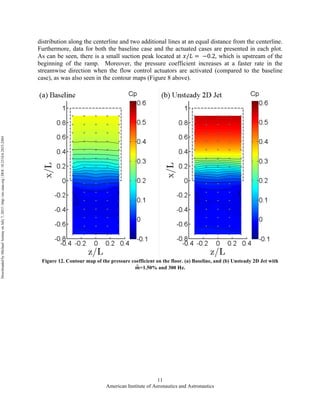
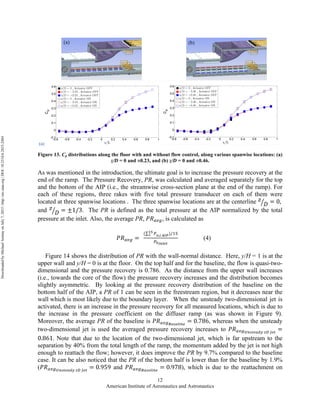
This document discusses an experimental study of flow control techniques in a transonic diffuser. A new diffuser design was created with an upper ramp and straight floor to decouple the secondary flow structures from separation. Different flow control actuators including steady and unsteady jets were tested at the ramp. The actuators were able to delay separation on the ramp and increase pressure recovery by up to 9.7% compared to the baseline case without flow control. Sweeping and pulsed jet arrays performed better than a two-dimensional jet when all were operated at their maximum mass flow ratios. The results provide insights into controlling flows in short inlet ducts used on aircraft.