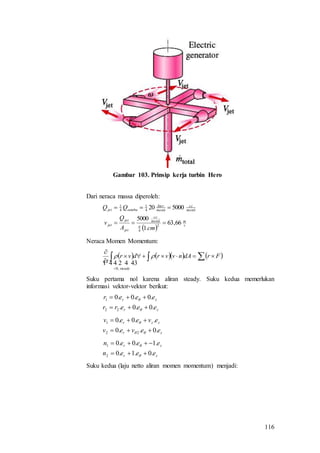
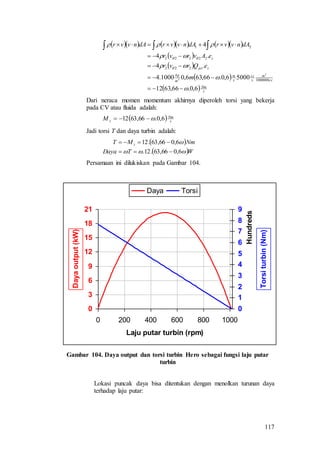
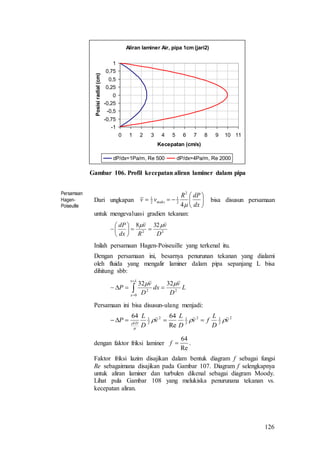
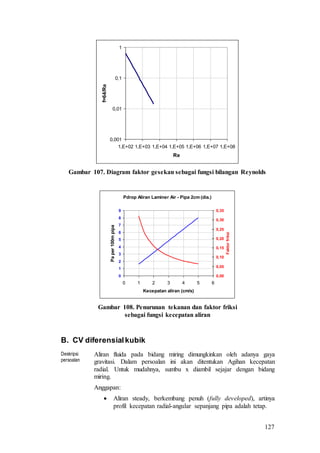
Dokumen ini adalah modul ajar untuk mata kuliah Mekanika Fluida yang disusun oleh Ir. Kutut Suryopratomo, M.T., M.Sc. Modul ini mencakup silabus, daftar isi, serta berbagai konsep dan hukum dasar terkait mekanika fluida, termasuk statika dan dinamika fluida, sifat-sifat fluida, dan analisis aliran. Terdapat juga informasi mendetail mengenai metode pengukuran dan teori teori yang mendasari aliran dalam berbagai konteks.










































































































































































 = 1 atau [orde (1/Re)]
= ’2 sebab nilai ’2 << 1.
Analisis orde
nilai pers.
Momentum-y
Terakhir, kita tinjau orde nilai suku-suku dalam persamaan
momentum-y:
2
2
2
2
'
'
'
'
Re
1
'
'
'
'
'
'
'
'
'
'
y
v
x
v
y
p
y
v
v
x
v
u
t
v
1) Orde nilai (v’/t’) adalah
'
1
'
0
0
nilaiorde
nilaiorde
v
ULUL
Uv
t
v
t
v
ee
e
2) Orde nilai suku konveksi '
1
'
1
'
'
'
x
v
u
3) Orde nilai suku konveksi '1'
'
'
'
y
v
v
4) Orde nilai suku difusi
'
01
0'
'nilaiorde
''nilaiorde
'
'
2
2
x
xv
x
v
5) Orde nilai suku difusi
'
1
0'
01
'nilaiorde
''nilaiorde
'
'
2
2
y
yv
y
v
6) Orde nilai suku gradien tekanan ditentukan dengan cara
berikut. Di tepi luar lapisan batas, arus mengalir bebas dari
pengaruh viskositas, sehingga andil gaya viskos dalam
persamaan momentum menjadi tidak signifikan atau
'
'
'
'
'
'
'
'
'
'
'''
y
p
y
u
v
x
v
u
t
v
. Karena orde sisi kiri harus harus
sama dengan sisi kanan, maka orde nilai
'
'
y
p
pastilah ’ juga.
7) Orde nilai (1/Re) telah ditentukan sebesar ’2.
Orde nilai
suku-suku
pers. N-S
Berikut bisa dilihat persamaan nir-dimensi N-S dengan orde nilai
dituliskan dalam tanda kurung di atas tiap-tiap suku:
1) kontinuitas:
0
'
'
'
'
11
y
v
x
u
2) momentum-x:
2
2 11
2
2
2
2
1'
1'111
'
'
'
'
Re
1
'
'
'
'
'
'
'
'
'
'
y
u
x
u
x
p
y
u
v
x
u
u
t
u](https://image.slidesharecdn.com/modul-mekanikafluida-rev02-161021095350/85/Modul-mekanika-fluida-rev-02-201-320.jpg)









![200
biasa disebut dengan istilah faktor gesekan, f. Dengan demikian
persoalan dipermudah menjadi penentuan nilai faktor gesekan
sebagai fungsi (/D) dan Re – dua variabel bebas saja!
B. Faktor Gesekan
2 macam
faktor
gesekan
Cara penyajian data faktor gesekan ada dua macam, yaitu:
Faktor gesekan Fanning, fF (= f/2), untuk pemakaian dengan
rumus: hL = 2fF (V2/g).(L/D).
Faktor gesekan Darcy, fD (= 2f), untuk pemakaian dengan
rumus: hL = fD (V2/2g).(L/D).
Perlu dicatat bahwa:
fF = Cf (koefisien gesekan kulit – skin friction coefficient).
fD = 4.fF.
Dengan demikian, di dalam pemakaian data faktor gesekan harus
diperhatikan definisi mana yang dipakai – apakah definisi Fanning
atau Darcy.
C. KerugianHead
Kerugian
pada Pipa
Lurus
Dari analisis neraca energi dan persamaan Hagen-Poiseuille:
hL = 32 VL / (gD2)
atau dalam notasi fF:
hL = 32 [/(VD)] . (L/D) . (V2/g) = (32/Re) . (L/D) . (V2/g)
Pembandingan dengan rumus Fanning menunjukkan bahwa:
(32 / Re) = 2fF
atau
fF = 16 / Re
untuk aliran laminer.
Bagaimana dengan fF untuk aliran turbulen?
Nilai fF bisa ditentukan melalui eksperimen sebagai fungsi (/D) dan
Re. Berikut adalah angkuman faktor gesekan Fanning untuk segala
macam aliran:
Aliran Laminer (Re < 2300):
fF = 16 / Re.
Aliran Turbulen (Pipa halus, Re > 3000):
fF
–(1/2) = 4.0 log10{Re.fF
(1/2)} – 0.40](https://image.slidesharecdn.com/modul-mekanikafluida-rev02-161021095350/85/Modul-mekanika-fluida-rev-02-212-320.jpg)
}, (teliti 1.5%)
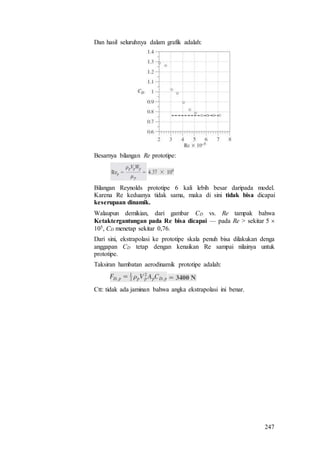
Sejauh ini telah dibicarakan perhitungan rugi-rugi aliran di dalam
pipa lurus, lantas bagaimana dengan bentuk pipa yang tidak lurus
(sambungan, belokan, dan katup)?
Kerugian
pada Fitting
Untuk memperhitungkan rugi-rugi karena bentuk dipakai hubungan
berikut yang sepadan bentuknya dengan rumus Fanning:
hL = 2fF (V2/g).(Leq/D)
dengan Leq = panjang ekuivalen, yaitu panjang pipa lurus yang
menghasilkan rugi-rugi sebesar rugi-rugi karena bentuk saluran; atau
dengan rumus:
hL = P / (.g) = K (V2/g)
dengan K = koefisien rugi-rugi yang tergantung pada macam
sambungan (fitting).
Data-data K dan (Leq/D) untuk beberapa macam sambungan
diperlihatkan pada Tabel 5.
Tabel 5. Koefisien rugi dan panjang ekuivalen
Sambungan (fitting) K Leq/D
Belokan 180o 1.6 75
Belokan 90o baku 0.7 32
Belokan 45o baku 0.35 15
Katup gate, bukaan ¼ 20 900
Katup gate, bukaan ½ 4.4 200
Katup gate, bukaan ¾ 0.85 40
Kerugian
pada Pipa
Penampang
Sembarang
Terakhir, bagaimana perhitungan rugi-rugi untuk saluran yang
penampangnya tidak bundar?
Jawabnya: semua hubungan untuk pipa bundar bisa tetap digunakan
untuk saluan berpenampang sembarang dengan sekedar mengganti
diameter D dalam rumus dengan diameter-ekuivalen Deq yang
didefinisikan sebagai:
Deq = 4 (Luas potongan-melintang aliran) / (Keliling-saluran
yang dibasahi)](https://image.slidesharecdn.com/modul-mekanikafluida-rev02-161021095350/85/Modul-mekanika-fluida-rev-02-213-320.jpg)
![202
Keliling-saluran yang dibasahi fluida biasa disebut juga sebagai “jari-
jari hidrolik, Rh.” Contoh perhitungan Deq untuk pipa konsentris
dengan garis-tengah luar Do dan garis-tengah dalam Di adalah:
Luas potongan-melintang aliran = (Do
2 – Di
2)/4
Keliling-saluran yang dibasahi, Rh = (Do + Di)
Deq = 4 [(Do
2 – Di
2)/4] / [(Do + Di)]
Deq = Do – Di
D. Macam Persoalan Aliran
3 Macam
Persoalan
Faktor gesekan terkait dengan enam parameter aliran, yaitu:
1) Diameter pipa, D
2) Kecepatan rerata, v
3) Densitas fluida,
4) Viscositas fluida,
5) Kekasaran pipa,
6) Rugi-rugi gesekan per satuan massa.
Jadi, jika diketahui 5 dari keenamnya maka satu parameter sisanya
bisa diperoleh dengan menggunakan diagram faktor-gesekan.
Ada tiga macam persoalan yang paling lazim, yaitu:
Macam 1: Diketahui: D, , , , Q Dicari: hf
Macam 1: Diketahui: D, , , , hf Dicari: Q
Macam 1: Diketahui: , , , hf, Q Dicari: D
Persoalan macam-1 bisa diselesaikan secara langsung, sedangkan
macam-2 dan 3 memerlukan coba-coba (trial and error).
Tiga persoalan dasar yang biasa dijumpai dalam perhitungan aliran-
pipa adalah sebagai berikut. Nilai parameter , , g, dan L sudah
tertentu.
1) Diketahui D, v (atau Q), hitung penurunan tekanan (persoalan
penurunan-tekanan).
2) Diketahui D, P, hitung kecepatan atau laju aliran (persoalan
laju-aliran).
3) Diketahui Q, P, hitung diameter D pipa (persoalan
penentuan ukuran pipa – sizing problem)
E. PengukuranAliran
Venturi meter Dalam alat ukur ini (Gambar 140) fluida dipercepat oleh karena](https://image.slidesharecdn.com/modul-mekanikafluida-rev02-161021095350/85/Modul-mekanika-fluida-rev-02-214-320.jpg)





















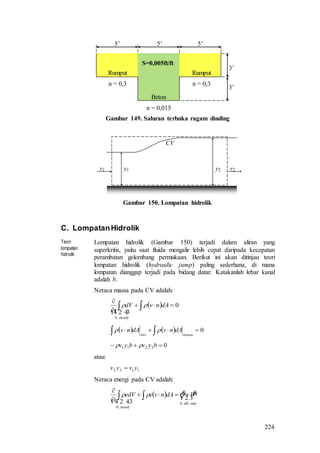










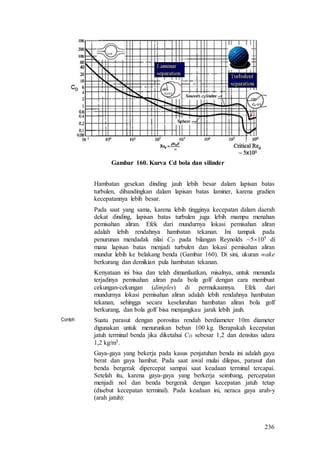

![238
MODUL XIII.
KESERUPAAN & PEMODELAN
Deskripsi
Mekanika dikembangkan melalui pasangan metode teoritik dan eksperimental
yang keduanya saling melengkapi. Eksperimen yang berhasil memerlukan
perencanaan yang baik. Sebagai bagian penting dari perencanaan eksperimen
adalah analisis dimensional. Analisis dimensional memungkinkan reduksi jumlah
variabel berdimensi yang terlibat dalam eksperimen. Dengan demikian
eksperimen bisa dilaksanakan dengan jauh lebih efisien.
Sasaran belajar:
16. Menjelaskan pengertian dimensi, dimensi dasar, dimensi turunan, dan
sistem satuan
17. Menjelaskan kepentingan dan melakukan analisis dimensional
18. Membedakan keserupaan geometrik, kinematik, dinamik, dan keserupaan
total antara model dan prototip
19. Melakukan penskalaan dari model ke prototip
A. Dimensi
Dimensi Dimensi adalah ukuran kuantitas fisis semisal panjang, waktu,
massa. Satuan adalah pemberian angka pada suatu dimensi, misalnya
panjang dalam m, waktu dalam detik, dan massa dalam kg.
Dimensi ada 2 macam, yaitu:
1. Dimensi primer/dasar (fundamental)
2. Dimensi sekunder/turunan
Dimensi
dasar &
turunan
Dimensi dasar ada 7, yaitu:
1. Massa m (kg)
2. Panjang L (m)
3. Waktu t (sec)
4. Suhu T (K)
5. Arus listrik I (A)
6. Jumlah cahaya C (cd)
7. Jumlah materi N (mol)
Ketujuh dimensi dasar ini bisa dikombinasikan untuk membentuk
semua dimensi turunan. Contoh:
[Kecepatan] = [Panjang/Waktu] = [L/t]
[Gaya] = [Massa Panjang/Waktu2] = [mL/t2]
Penentuan
dimensi
dasar
Dimensi yang dipandang dasar atau fundamental sebenarnya dipilih
begitu saja. Ilustrasinya demikian. Luas A adalah karakteristik yang
bisa diukur dari suatu objek, dan berarti luas adalah dimensi.](https://image.slidesharecdn.com/modul-mekanikafluida-rev02-161021095350/85/Modul-mekanika-fluida-rev-02-250-320.jpg)