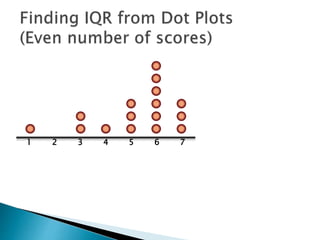
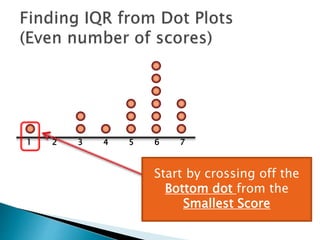
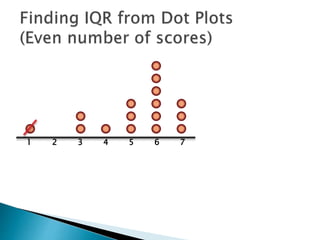
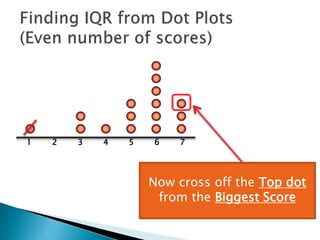
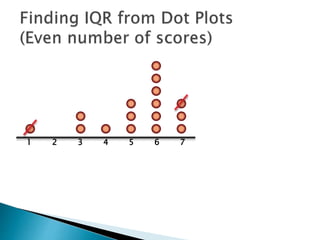
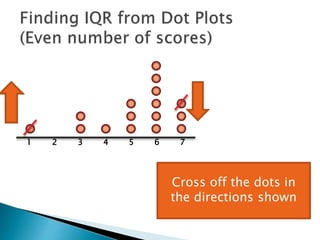
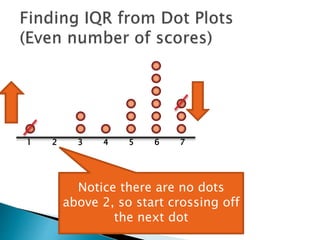
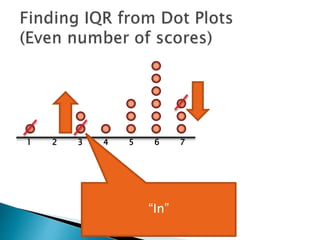
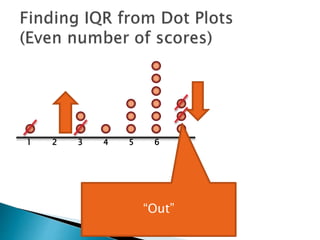
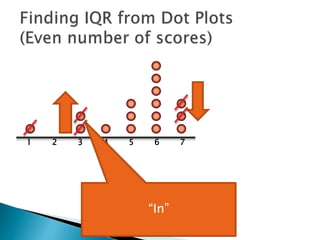
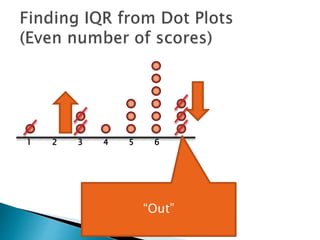
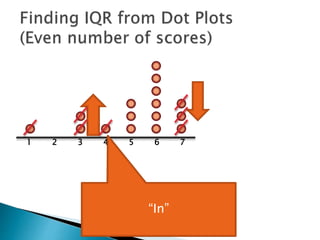
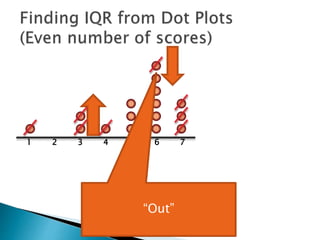
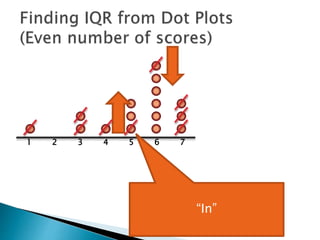
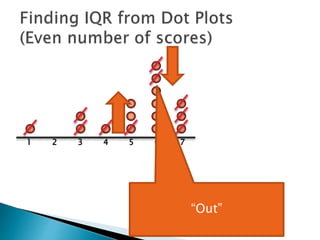
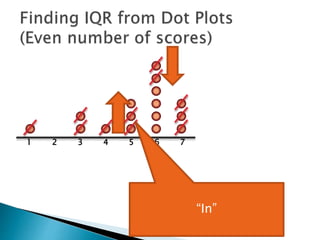
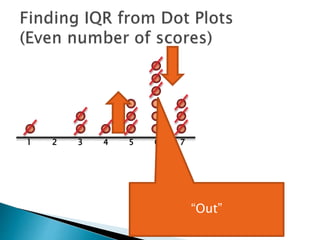
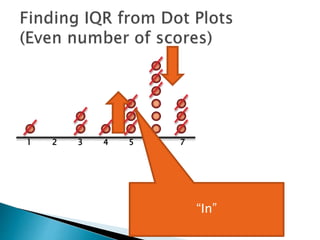
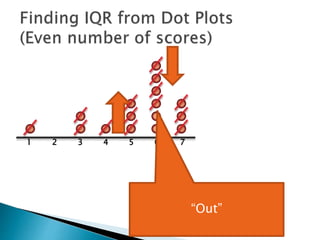
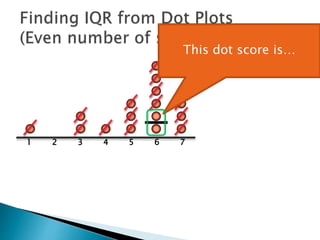
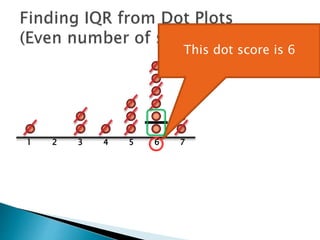
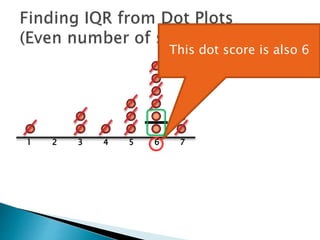
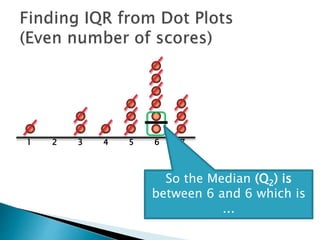
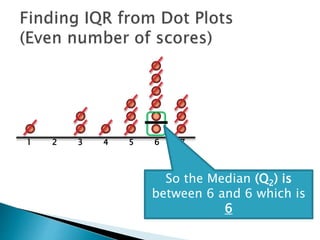
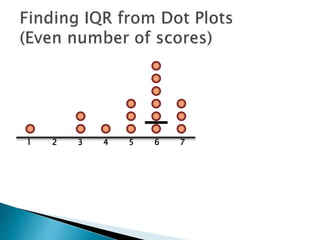
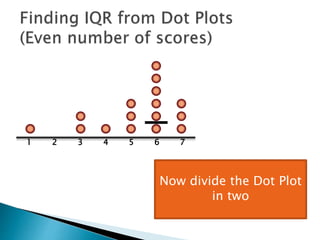
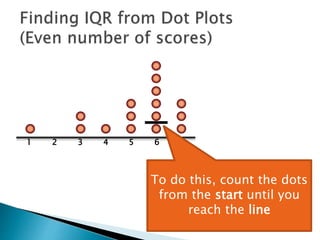
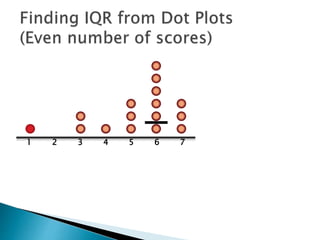
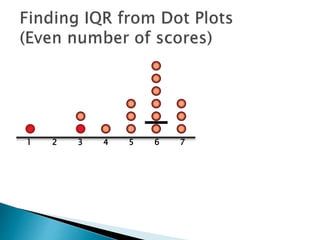
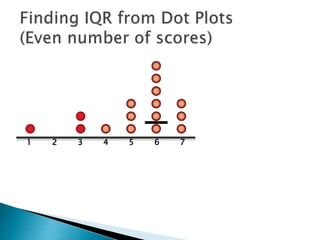
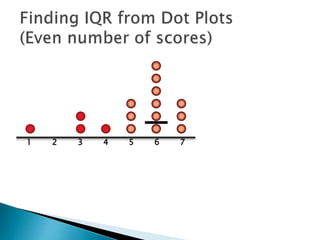
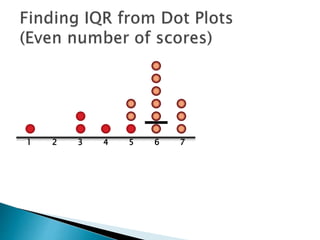
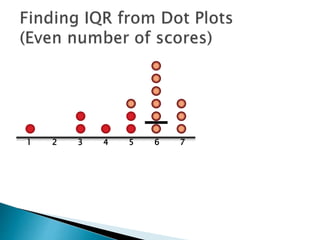
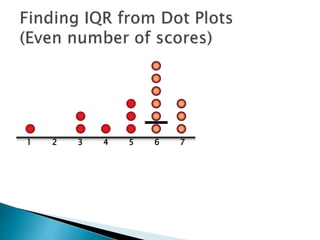
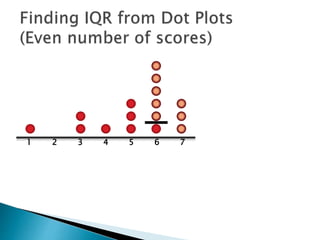
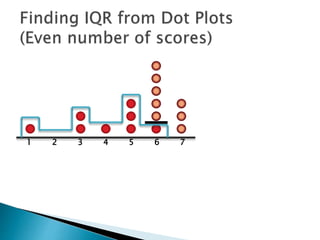
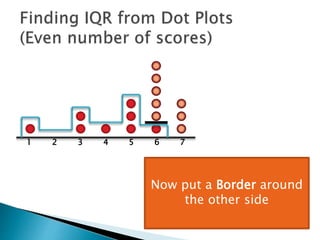
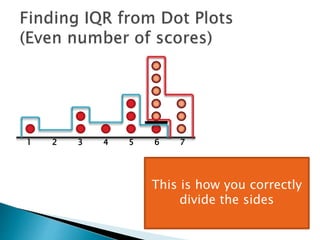
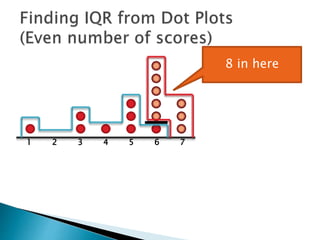
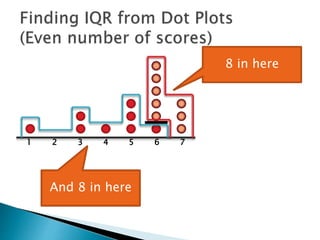
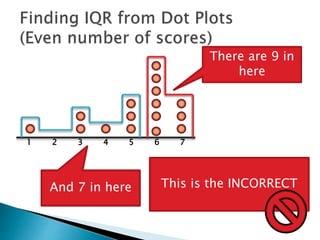
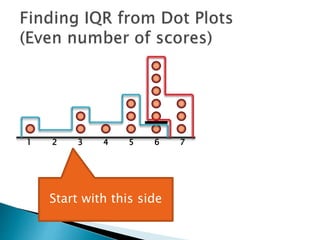
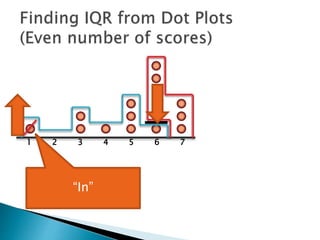
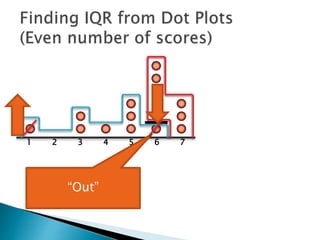
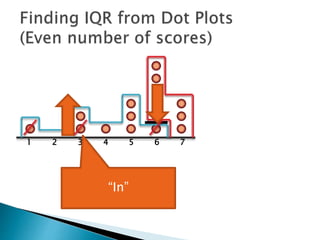
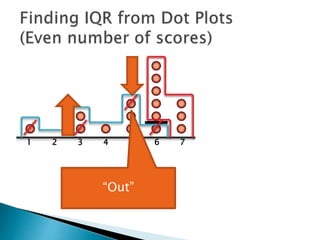
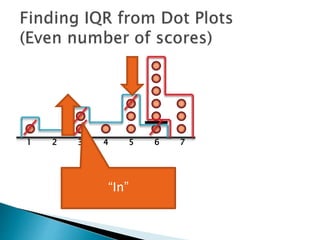
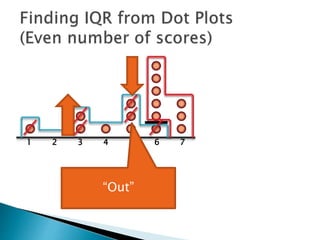
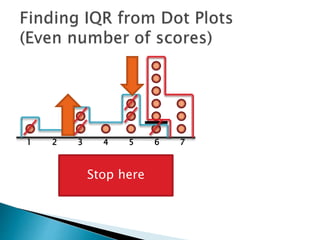
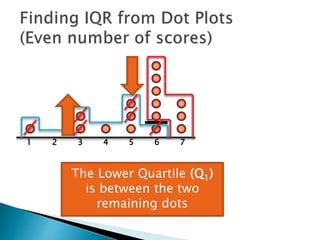
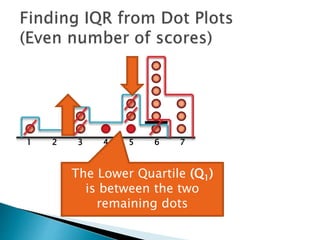
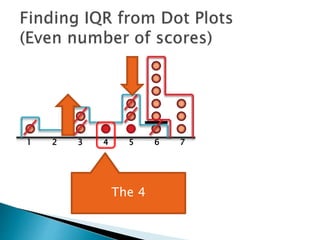
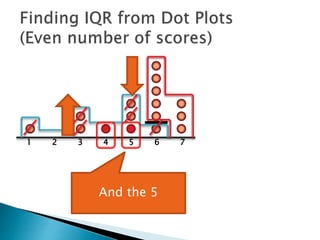
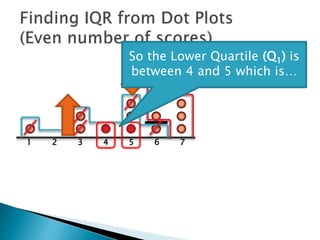
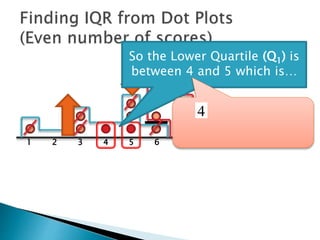
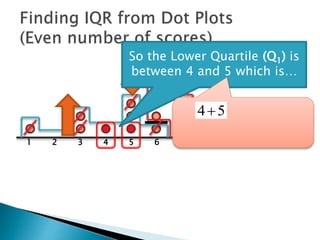
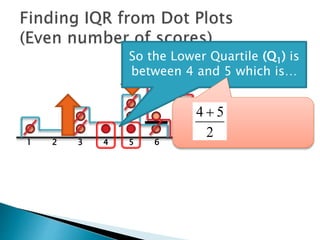
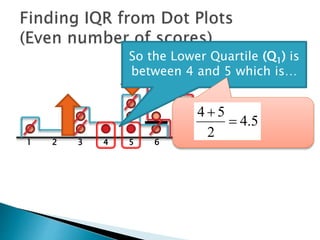
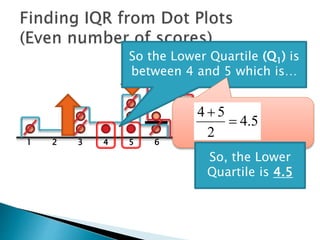
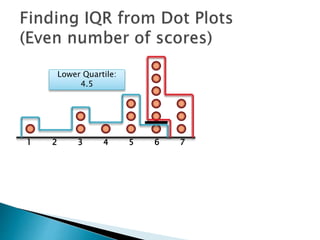
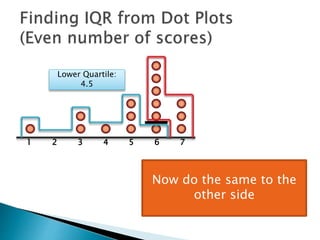
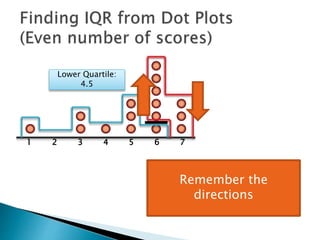
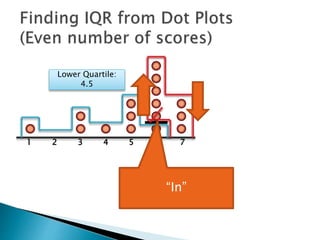
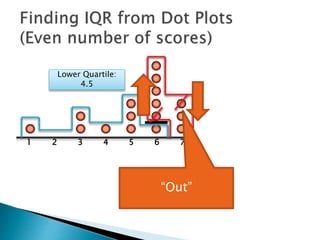
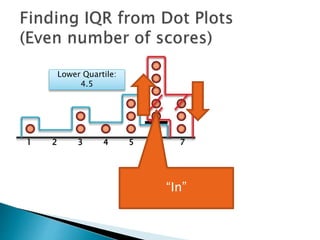
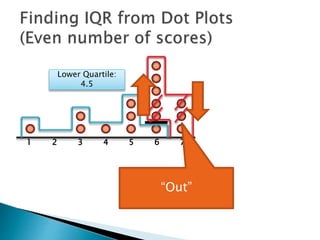
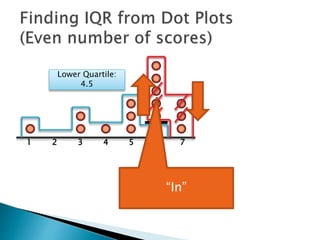
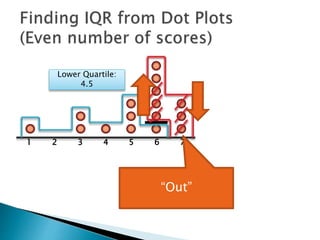
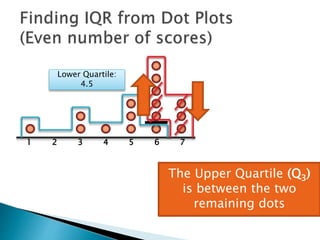
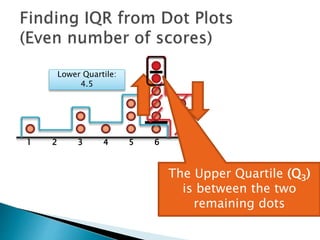
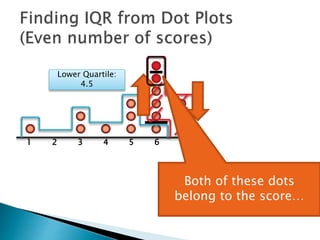
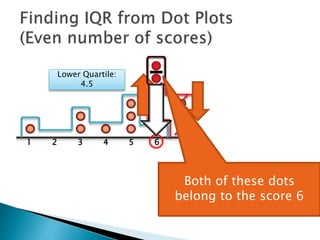
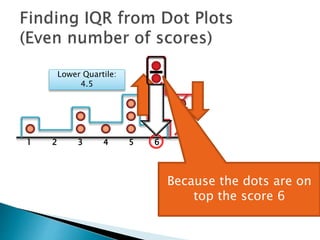
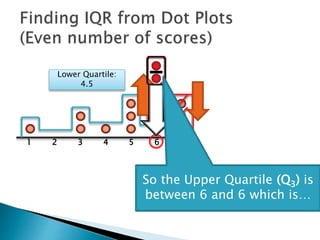
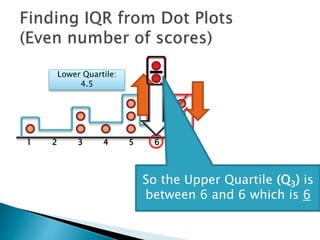
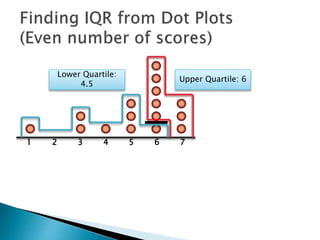
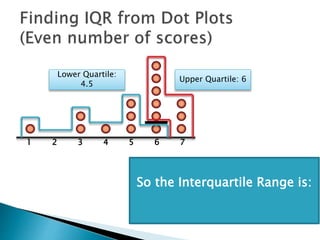
The document explains how to find the interquartile range (IQR) from a set of even-numbered scores using a dot plot. It outlines the steps for determining the median, lower quartile (Q1), upper quartile (Q3), and subsequently calculating the IQR. The final calculated IQR is 1.5.

1. - Mr Kim

2. Finding IQR for even number of scores

3. 1 2 3 4 5 6 7

4. 1 2 3 4 5 6 7
Here is a Dot Plot

5. 1 2 3 4 5 6 7
First, find the Median by
crossing off the dots

6. 1 2 3 4 5 6 7
Start by crossing off the
Bottom dot from the
Smallest Score

7. 1 2 3 4 5 6 7
Start by crossing off the
Bottom dot from the
Smallest Score

8. 1 2 3 4 5 6 7

9. 1 2 3 4 5 6 7
Now cross off the Top dot
from the Biggest Score

10. 1 2 3 4 5 6 7
Now cross off the Top dot
from the Biggest Score

11. 1 2 3 4 5 6 7

12. 1 2 3 4 5 6 7
Cross off the dots in
the directions shown

13. 1 2 3 4 5 6 7
Notice there are no dots
above 2, so skip to the next
dot

14. 1 2 3 4 5 6 7
Notice there are no dots
above 2, so skip to the next
dot

15. 1 2 3 4 5 6 7
“In”

16. 1 2 3 4 5 6 7
“Out”

17. 1 2 3 4 5 6 7
“In”

18. 1 2 3 4 5 6 7
“Out”

19. 1 2 3 4 5 6 7
“In”

20. 1 2 3 4 5 6 7
“Out”

21. 1 2 3 4 5 6 7
“In”

22. 1 2 3 4 5 6 7
“Out”

23. 1 2 3 4 5 6 7
“In”

24. 1 2 3 4 5 6 7
“Out”

25. 1 2 3 4 5 6 7
“In”

26. 1 2 3 4 5 6 7
“Out”

27. 1 2 3 4 5 6 7
Stop here

28. 1 2 3 4 5 6 7
Always stop at “Out”

29. 1 2 3 4 5 6 7
Now, put a line between
the two dots

30. 1 2 3 4 5 6 7
Now, put a line between
the two dots

31. 1 2 3 4 5 6 7
The Median is between
those two dots

32. 1 2 3 4 5 6 7
This dot is…

33. 1 2 3 4 5 6 7
This dot is 6

34. 1 2 3 4 5 6 7
This dot is…

35. 1 2 3 4 5 6 7
This dot is also 6

36. 1 2 3 4 5 6 7
So the Median (Q2) is
between 6 and 6 which is
…

37. 1 2 3 4 5 6 7
So the Median (Q2) is
between 6 and 6 which is
6

38. 1 2 3 4 5 6 7

39. 1 2 3 4 5 6 7
Now divide the Dot Plot
in two

40. 1 2 3 4 5 6 7
**It is very important to
divide the sides properly

41. 1 2 3 4 5 6 7
To do this, count the dots
from the start until you
reach the line

42. 1 2 3 4 5 6 7

43. 1 2 3 4 5 6 7

44. 1 2 3 4 5 6 7

45. 1 2 3 4 5 6 7

46. 1 2 3 4 5 6 7

47. 1 2 3 4 5 6 7

48. 1 2 3 4 5 6 7

49. 1 2 3 4 5 6 7

50. 1 2 3 4 5 6 7
Stop here

51. 1 2 3 4 5 6 7
Now put a Border around
the dots that you just
counted

52. 1 2 3 4 5 6 7

53. 1 2 3 4 5 6 7
Now put a Border around
the other side

54. 1 2 3 4 5 6 7

55. 1 2 3 4 5 6 7
This is how you correctly
divide the sides

56. 1 2 3 4 5 6 7
Notice there are
8 dots on each side

57. 1 2 3 4 5 6 7
8 in here

58. 1 2 3 4 5 6 7
8 in here
And 8 in here

59. 1 2 3 4 5 6 7
This is the INCORRECT

60. 1 2 3 4 5 6 7
Do you notice
the difference?
This is the INCORRECT

61. 1 2 3 4 5 6 7
This is the INCORRECT
There are 9 in
here
And 7 in here

62. 1 2 3 4 5 6 7
Now find the Median for
both sides of the dots

63. 1 2 3 4 5 6 7
Start with this side

64. 1 2 3 4 5 6 7
Remember the
directions

65. 1 2 3 4 5 6 7
“In”

66. 1 2 3 4 5 6 7
“Out”

67. 1 2 3 4 5 6 7
“In”

68. 1 2 3 4 5 6 7
“Out”

69. 1 2 3 4 5 6 7
“In”

70. 1 2 3 4 5 6 7
“Out”

71. 1 2 3 4 5 6 7
Stop here

72. 1 2 3 4 5 6 7
The Lower Quartile (Q1)
is between the two dots

73. 1 2 3 4 5 6 7
The Lower Quartile (Q1)
is between the two dots

74. 1 2 3 4 5 6 7
The 4

75. 1 2 3 4 5 6 7
And the 5

76. 1 2 3 4 5 6 7
So the Lower Quartile (Q1) is
between 4 and 5 which is…

77. 1 2 3 4 5 6 7
So the Lower Quartile (Q1) is
between 4 and 5 which is 4.5

78. 1 2 3 4 5 6 7
Lower Quartile:
4.5

79. 1 2 3 4 5 6 7
Lower Quartile:
4.5
Now cross off the other
side

80. 1 2 3 4 5 6 7
Lower Quartile:
4.5
Remember the
directions

81. 1 2 3 4 5 6 7
Lower Quartile:
4.5
“In”

82. 1 2 3 4 5 6 7
Lower Quartile:
4.5
“Out”

83. 1 2 3 4 5 6 7
Lower Quartile:
4.5
“In”

84. 1 2 3 4 5 6 7
Lower Quartile:
4.5
“Out”

85. 1 2 3 4 5 6 7
Lower Quartile:
4.5
“In”

86. 1 2 3 4 5 6 7
Lower Quartile:
4.5
“Out”

87. 1 2 3 4 5 6 7
Lower Quartile:
4.5
Stop here

88. 1 2 3 4 5 6 7
Lower Quartile:
4.5
The Upper Quartile (Q3)
is between the two dots

89. 1 2 3 4 5 6 7
Lower Quartile:
4.5
The Upper Quartile (Q3)
is between the two dots

90. 1 2 3 4 5 6 7
Lower Quartile:
4.5
Both of these dots
belong to the score…

91. 1 2 3 4 5 6 7
Lower Quartile:
4.5
Both of these dots
belong to the score 6

92. 1 2 3 4 5 6 7
Lower Quartile:
4.5
So the Upper Quartile (Q3) is
between 6 and 6 which is…

93. 1 2 3 4 5 6 7
Lower Quartile:
4.5
So the Upper Quartile (Q3) is
between 6 and 6 which is 6

94. 1 2 3 4 5 6 7
Lower Quartile:
4.5
Upper Quartile: 6

95. 1 2 3 4 5 6 7
Lower Quartile:
4.5
Upper Quartile: 6
So the Interquartile Range is:

96. 1 2 3 4 5 6 7
Lower Quartile:
4.5
Upper Quartile: 6
So the Interquartile Range is:

97. 1 2 3 4 5 6 7
Lower Quartile:
4.5
Upper Quartile: 6
So the Interquartile Range is:
6 -

98. 1 2 3 4 5 6 7
Lower Quartile:
4.5
Upper Quartile: 6
So the Interquartile Range is:
6 -

99. 1 2 3 4 5 6 7
Lower Quartile:
4.5
Upper Quartile: 6
So the Interquartile Range is:
6 – 4.5

100. 1 2 3 4 5 6 7
Lower Quartile:
4.5
Upper Quartile: 6
So the Interquartile Range is:
6 – 4.5 = 1.5
Our Final Answer!