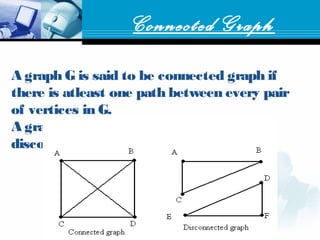
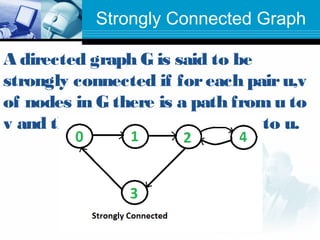
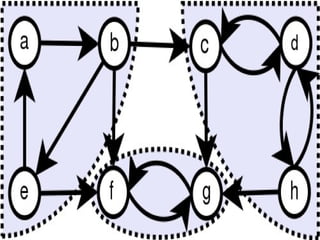
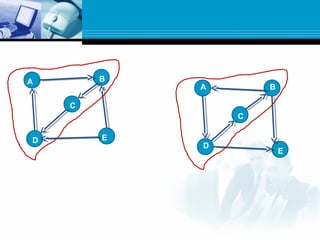
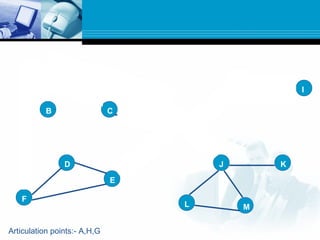
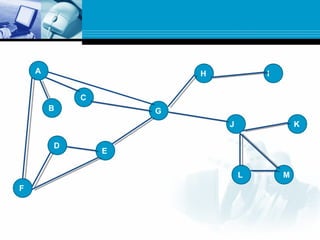
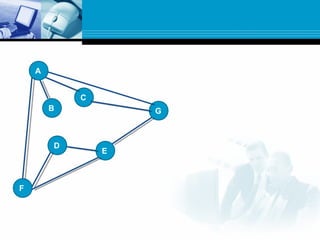
A graph is a data structure consisting of nodes connected by edges. There are different types of graphs such as undirected graphs, directed graphs, connected graphs, and strongly connected graphs. Algorithms like depth-first search, Kosaraju's algorithm, and Warshall's algorithm can be used to find strongly connected components, biconnected components, and shortest paths in graphs.

1. Company
LOGO
Presentation Topic

2. What is a Graph?
 A data structure that consists of a set of nodes
(vertices) and a set of edges that relate the nodes to
each other
 The set of edges describes relationships among the
vertices

3. A graph G consists of two things:
1.A set V of elements called nodes(or points or vertices)
2.A set E of edges such that each edge e in E is identified with a unique pair
[u,v] of nodes in V, denoted by e=[u,v]
Suppose e=[u,v]. Then the nodes u and v are called endpoints of e and u and v
are said to be adjacent nodes or neighbors.

4. Node or
Point or
vertex
Edge
u
v
e=[u,v]
Adjacentnodesorneighbors

5. Degree of a graph
The degree of a node u, written as deg(u), is the
number of edges containing u.
If deg(u)=0 that is, if u does not belong to any
edge then u is called an isolated node.
A
B C
D
E
Nodes degree
A 4
B 3
C 2
D 3
E 4
F 0F
Isolated node

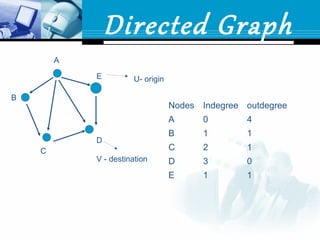
6. Directed Graph
 Each edge is assigned a direction or each edge E is
identified with ordered pair (u,v)
 (u,v) directed graph
 [u,v] undirected graph
 U=origin
 v=destination

7. Connected Graph
A graph G is said to be connected graph if
there is atleast one path between every pair
of vertices in G.
A graph which is not connected is called
disconnected graph.

8. Strongly Connected Graph
A directed graph G is said to be
strongly connected if foreach pairu,v
of nodes in G there is a path fromu to
v and there is also a path fromv to u.

9. Strongly Connected Components
A strongly connected component of a directed graph G is a
subgraph that is strongly connected, and
is maximal with this property:
no additional edges or vertices from G can be included in the
subgraph without breaking its property of being strongly
connected.
 The collection of strongly connected components forms
a partition of the set of vertices of G.

10. In simple words,
A strongly connected component (SCC) of a
directed graph is a maximal strongly connected subgraph.

12. Depth-First-Search
(DFS)
 The idea behind DFS is travel as far as
you can down a path
 DFS can be implemented efficiently using
a stack .
 This algorithm is similar to inorder
traversal of a binary tree i.e. first of all we
process the left node then root and then
the right node.

13. J
print
J
D
K
K
E
G
G
C
C
F
F E D

14. Kosaraju's algorithm
 Kosaraju's algorithm (also known as
the Kosaraju–Shariralgorithm) is a linear
time algorithm to find the strongly
connected components of a directed
graph.
 It makes use of the fact that
the transpose graph (the same graph with
the direction of every edge reversed) has

15. Algorithm
1) Let G be a directed graph and S be an empty stack.
2) Perform a depth-first search starting from any v.
3) Reverse the directions of all arcs to obtain the transpose
graph.
4) Again perform depth-first search on transpose graph.

16. A B
C
D E
A B
C
D
E

17. A group of people are generally strongly connected (For example,
students of a class or any other common place). Many people in
these groups generally like some common pages or play common
games. The SCC algorithms can be used to find such groups and
suggest the commonly liked pages or games to the people in the
group who have not yet liked commonly liked a page or played a
game.
Use of SCC algorithm in Social life

18. MultigraphMultigraph
 A graph G is said to be a multigraph if itA graph G is said to be a multigraph if it
has:has:
1.1. multiple edgesmultiple edges
2.2. LoopsLoops
A
B C
D
e1
e7 e6
e5
e4
e3
e2

19. Directed Graph
 A directed graph G also called a digraph
or graph is the same as multigraph
except that each edge in G is assigned a
direction.
Outdegree= number of outgoing edges
Indegree= number of incoming edges

20. U- origin
V - destination
A
B
C
D
E
Nodes Indegree outdegree
A 0 4
B 1 1
C 2 1
D 3 0
E 1 1
Directed Graph

21. Connected Graph
A graph G is said to be connected graph if
there is atleast one path between every pair
of vertices in G.
A graph which is not connected is called
disconnected graph.

22. Articulation PointArticulation Point
 An articulation point in a connected graph
is a vertex that, if delete would break the
graph into two or more pieces (connected
components).

24. A
B
F
D
E
C
G
L
J
H I
K
M
Articulation points:- A,H,G

25. Biconnected GraphBiconnected Graph
 A graph with no articulation point is called
biconnected graph.
 In other words, a graph is biconnected if
and only if any vertex is deleted, the graph
remains connected.

26. A
B C
D

27. Biconnected Components
 A biconnected component of a graph is a
maximal biconnected subgraph.
 A biconnected subgraph that is not
properly contained in a larger biconnected
subgraph.

29. A
B
C
D
F
E
G
H I
J K
L M

30. A
B
C
D
F
E
G

31. A
B
C
F
E
G
If we delete D

32. A
B
C
D
F
G
If we delete E

33.  Let G be a directed graph with m nodes
v1,v2…….,vm. Suppose we want to find
the path matrix P of the graph G.
Warshall gave an alogrithm for this
purpose that is much more efficient than
calculating the powers of the adjacency
matrix A
Warshall’s Algorithm: Shortest Paths

34. Where adjacency matrix A =(aij) of the graph G is m x m
matrix defined as follows:
aij= 1 If vi is adjacent to vj, i.e. if there is an edge (vi,vj)
0 otherwise
such a matrix A, which contains entries of only 0 and 1, is called a
bit matrix or a boolean matrix

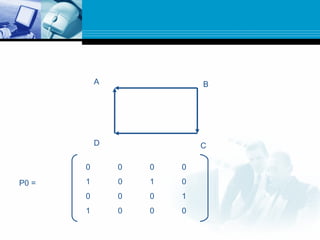
35.  This algorithm is used to find the shortest
paths in G when G is weighted.
 First we define m-square boolean matrices
P0,P1…….,Pm as follows:
 Let Pk[i,j] denote the i, j entry of the
matrix Pk.

36.  Then we define
 Pk[i,j]=
1 ,if there is a simple path from vi to vj which does
not use any other node except possibly v1,v2,
…..,vk
0 ,otherwise
In other words,
P0[i,j]=1, if there is an edge from vi to vj
P1[i,j]=1, if there is a simple path from vi to vj which does not use any other node
except possibly v1.
P2[i,j]=1, if there is a simple path from vi to vj which does not use any other node
except possibly v1 and v2.

37.  Observe that P0=A, the adjacency matrix of G.
 Since G has only m nodes, the last matrix
Pm=P, the path matrix of G.
 Warshall observed that Pk[i,j]=1 can occur only
if one of the following two cases occur:
1. There is a simple path from vi to vj which does
not use any other node except possibly v1,v2,
….,vk-1, hence
Pk-1[i,j]=1
vi ……….. vj

38. 2. There is a simple path from vi to vk and
a simple path from vk to vj where each
path does not use any other nodes
except possibly v1,v2,……,vk-1; hence
Pk-1[i,k]=1 and Pk-1[k,j]=1
vi ……….. ………..vk vj

39.  Accordingly, the elements of matrix Pk can
be obtained by:
Pk[i,j]=Pk-1[i,j] v (Pk-1[i,k] Pk-1[k,j])
Where V and denote the logical OR and AND operator
^ 0 1
0 0 0
1 0 1
v 0 1
0 0 1
1 1 1

40. A B
CD
0 0 0 0
1 0 1 0
0 0 0 1
1 0 0 0
P0 =

41.  P1[1,1]=P0[1,1]v(P0[1,1]^P0[1,1])
=0v(0^0)
=0v0=0
 P1[1,2]=P0[1,2]v(P0[1,1]^P0[1,2])
=0v(0^0)
=0v0=0
 P1[1,3]=P0[1,3]v(P0[1,1]^P0[1,3])
=0v(0^0)
=0v0=0
 P1[1,4]=P0[1,4]v(P0[1,1]^P0[1,4])
=0v(0^0)
=0v0=0
P1[2,1]=P0[2,1]v(P0[2,1]^P0[1,1])
=1v(1^0)
=1v0=1
P1[2,2]=P0[2,2]v(P0[2,1]^P0[1,2])
=0v(1^0)
=0v0=0
P1[2,3]=P0[2,3]v(P0[2,1]^P0[1,3])
=1v(1^0)
=1v0=1
P1[2,4]=P0[2,4]v(P0[2,1]^P0[1,4])
=0v(1^0)
=0v0=0
P1 =
0 0 0 0
1 0 1 0
- - - -
- - - -

42. Shortest path algorithm
 Let G be a directed graph with m nodes
v1,v2,…..vm.
 Suppose G is weighted i.e. suppose each
edge e in G is assigned a non negative
number w(e) called the weight or length of
the edge e.

43. Then G is maintained in memory by its
weight matrix W=(wij) defined as:
Wij= W(e), if there is an edge e from vi to vj
0, if there is no edge from vi to vj

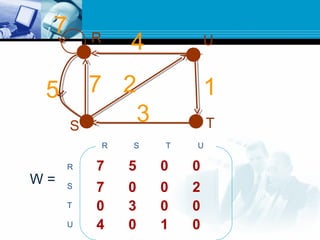
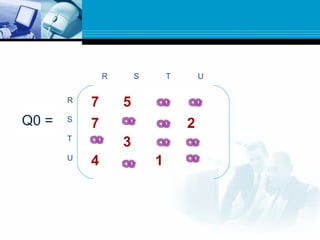
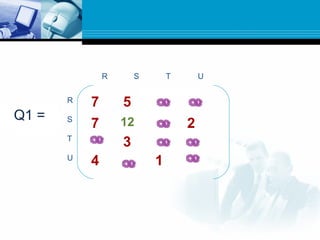
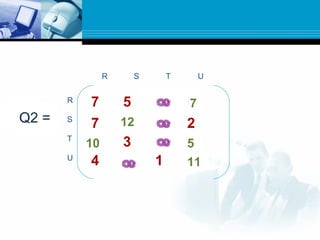
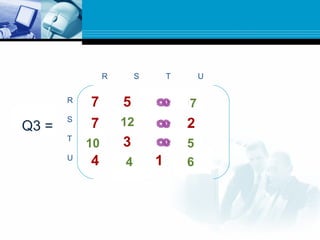
44.  Path matrix P tells us whether or not there are paths
between the nodes.
 Now we want to find a matrix Q which tell us the lengths of
the shortest paths between the nodes or a matrix Q=(qij)
where
qij= length of shortest path from vi to vj.
 Here we define a sequence of matrices Q1,Q2,…..Qm
defined as
Qk[i,j]= the smaller of the length of the preceding paths from
vi to vj or the sum of the lengths of preceeding paths from vi
to vk and from vk to vj.
Qk[i,j]=min(Qk-1[i,j],Qk-1[i,k]+Qk-1[k,j])

45. R U
S T
W =
R S T U
R
S
T
U
4
1275
3
7 5 0 0
7
7 0 0 2
0 3 0 0
4 0 1 0

46. R S T U
R
S
T
U
7 5 0 0
7 0 0 2
0 3 0 0
4 0 1 0
W =Q0 =

47. Q1(1,1) =MIN(Q0(1,1),Q0(1,1)+Q0(1,1))
=MIN(7,7+7)
=MIN(7,14)= 7
Q1(1,2) =MIN(Q0(1,2),Q0(1,1)+Q0(1,2))
=MIN(5,7+5)
=MIN(5,12)= 5
Q1(2,1) =MIN(Q0(2,1),Q0(2,1)+Q0(1,1))
=MIN(7,7+7)
=MIN(7,14)= 7
Q1(3,1) =MIN(Q0(3,1),Q0(3,1)+Q0(1,1))
=MIN( , +7)
=MIN( ,14 )= 7

48. R S T U
R
S
T
U
7 5 0 0
7 0 0 2
0 3 0 0
4 0 1 0
W =Q0 =Q1 = 12

49. Q2(1,1) =MIN(Q1(1,1),Q1(1,1)+Q1(1,1))
=MIN(7,5+7)
=MIN(7,12)= 7
Q1(1,3) =MIN(Q1(1,3),Q1(1,2)+Q1(2,3))
=MIN( , 5+ )
=MIN( ,14 )= 7
Similarly, proceeding like this we get a new matrix....

50. R S T U
R
S
T
U
7 5 0 0
7 0 0 2
0 3 0 0
4 0 1 0
W =Q0 =Q1 = 12Q2 =
10
7
5
11

51. Q3(1,1) =MIN(Q2(1,1),Q2(1,3)+Q2(3,1))
=MIN(7, +10)
=MIN(7, )= 7
Q3(2,1) =MIN(Q2(2,1),Q2(2,3)+Q2(3,1))
=MIN(7, +5)
=MIN(7, ) = 7
Q3(3,1) =MIN(Q2(3,1),Q2(3,3)+Q2(1,3))
=MIN(10, +7 )
=MIN(10,14 )= 10
Similarly, proceeding like this we get a new matrix....

52. R S T U
R
S
T
U
7 5 0 0
7 0 0 2
0 3 0 0
4 0 1 0
W = 12Q2 =
10
7
5
11
Q3 =
4 6

53. Q4(1,1) =MIN(Q3(1,1),Q3(1,4)+Q3(4,1))
=MIN(7,7+4)
=MIN(7,11)= 7
Q4(2,1) =MIN(Q3(2,1),Q3(2,4)+Q3(4,1))
=MIN(7,2+4)
=MIN(7,6)= 6
Q4(3,1) =MIN(Q3(3,1),Q3(2,4)+Q3(4,1))
=MIN(10,5+4)
=MIN(10,9)= 9

54. R S T U
R
S
T
U
7 5 0 0
7 0 0 2
0 3 0 0
4 0 1 0
W = 12Q2 =
10
7
5
11
Q3 =
4 6
Q4 = 3
8
6