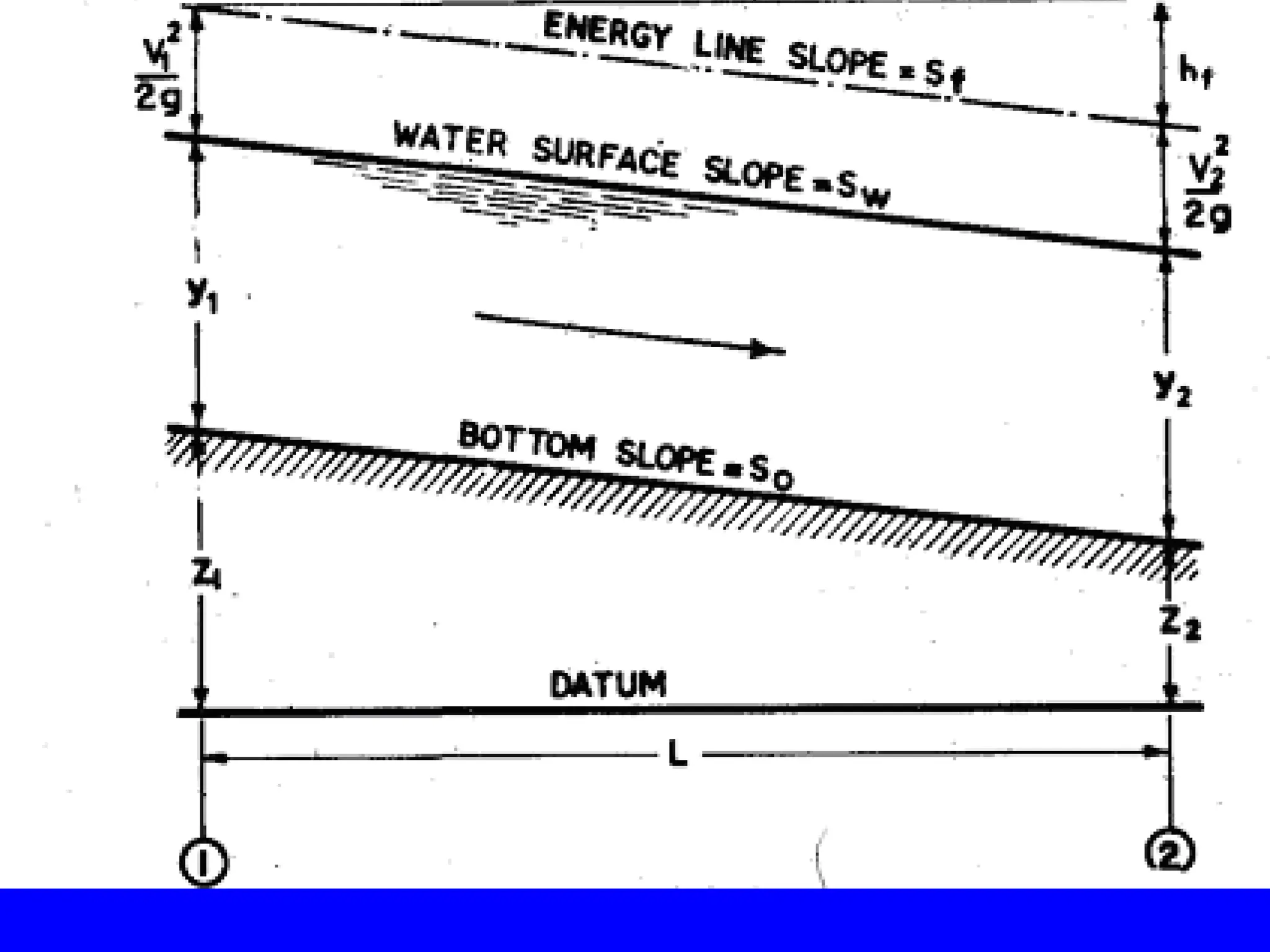
The document discusses types of flow in channels, distinguishing between uniform and non-uniform flow, as well as artificial and natural channels. It explains the mechanics of flow, including hydraulic gradients, energy lines, and the effects of resistance and gravity on flow characteristics. Additionally, it covers the classification of flow types based on depth change, flow stability, and the Reynolds and Froude numbers to assess flow conditions.

1. Lecture 21
Types of flow in channel – uniform flow –
most economical section of channel –
rectangular – trapezoidal

2. ➢ A channel may be defined as a passage through which
water flows under atmospheric pressure
➢ In the case of flow through a pipe there is no free
surface as in the case of flow through a channel. The
water level in the piezometric tube installed at different
sections of a pipe indicate the hydraulic gradient
➢ In the case of channel flow the water surface itself is
the hydraulic gradient

3. ➢ The total energy lines in both the cases lie at a distance
(V2/2g) above the hydraulic gradient at every section
➢ In order to overcome the resistance and to cause the flow
of water in a channel, it is constructed with bottom sloping
towards the direction of flow
➢ Thus a component of the weight of the flowing water in the
direction of flow is developed which cause the flow of water
in the channel.

5. A natural channel is the one which has irregular
sections of varying shapes, which is developed in
natural way. The examples of natural channels are
rivers, streams etc.
An artificial channel is the one which is built
artificially for carrying water for various purposes.
Obviously artificial channels have their cross
sections with regular geometrical shapes, which
usually remain so throughout the length of the
channel.
The artificial channels may be further classified
according to the shape of the cross-section as,
rectangular channel, trapezoidal channel, triangular
channel, parabolic channel, and circular channel

6. The artificial channels may be further
classified according to the shape of the
cross-section as, rectangular channel,
trapezoidal channel, triangular channel,
parabolic channel, and circular channel

7. The channels without any cover at the top are
known as open channels.
The channels having cover at the top are known as
closed channels. However, the closed channels will
always be running partly full of water, in order that
the flow may be a channel flow with atmospheric
pressure prevailing over its entire top surface.
Some of the common examples of closed channels
are closed conduits or pipes flowing partly full of
water, underground drains, tunnels etc., not running
full of water.

8. A channel having the same shape of various
sections along its length and laid on a
constant bottom slope is known as prismatic
channel, otherwise the channel is non-
prismatic.

9. The flow in channels can be classified into following types
depending upon the change in the depth of flow with respect
to space and time.
Flow in a channel is said to be steady if the flow
characteristics at any point do not change with time that is
(∂V/∂t) = 0, (∂y/∂t) = 0 etc.
if any of the flow characteristics changes with time the flow is
unsteady.
Flow in a channel is said to be uniform if the depth, slope,
cross-section and velocity remain constant over a given
length of the channel.
Flow in channels is termed as non-uniform or varied if the
depth of flow y, changes from section to section, along the
length of the channel, that is (∂y/∂s) is not equal to zero.

10. Varied flow may be further classified as rapidly
varied flow (RVF) and gradually varied flow (G.V.F.).
If the depth of flow changes abruptly over a
comparatively short distance, the flow is
characterised as a rapidly varied flow. Typical
examples of rapidly varied flow are hydraulic jump
and hydraulic drop.
In a gradually varied flow the change in the depth
takes place gradually in a long reach of the channel.

11. Just as in pipe in channels may also be
characterized as laminar, turbulent or in a
transitional state, depending on the relative effect of
viscous and inertia forces.
In channels, the Reynolds number for flow in
channel is commonly defined as
Re = ρVR/ μ
where V is the mean velocity of flow,
R is the hydraulic radius of the channel section and
ρ and μ, are the mass density and absolute viscosity
of water.

12. Re equal to 500 to 600 the flow may be
considered to be laminar
Re greater than 2000 channels is turbulent.
Re in between 500 to 2000 the flow may be
considered to be in transitional state.

13. The gravity is a predominant force in the case of channel
depending on the relative effect of gravity and inertia
force flow may be designated as subcritical, critical or
supercritical.
The inertia and the gravity forces is another dimensionless
parameter called Froude number Fr which is defined as
gD
V
Fr =
where
V is the mean velocity of flow, m/s,
g is acceleration due to gravity and
D is hydraulic depth of the section.

14. When Fr = 1.0, the channel flow is said to be
in a critical state.
If Fr < 1.0 the flow is described as subcritical
or tranquil or streaming
if Fr>1.0 , the flow is said to be supercritical or
rapid or shooting

15. When water flows in an open channel
resistance is offered to it, which results
in causing a loss of energy.
The resistance encountered by the
flowing water is generally counteracted
by the components of gravity forces
acting on the body of the water in the
direction of motion.
A uniform flow will be developed if the
resistance is balanced by the gravity
forces

16. The magnitude of the resistance, when other
physical factors of the channel are kept
unchanged, depends on the velocity of flow.
When water enters the channel, the velocity
and hence the resistance are smaller than the
gravity forces, which results in an
accelerating flow in the upstream reach of the
channel.
The velocity and the resistance increase
gradually until a balance between the
resistance and gravity forces is reached.
From this point onwards the flow becomes
uniform.

18. The main features of uniform flow in a
channel can be summarised as follows:
(1) The depth of flow, wetted area,
velocity of flow and discharge are
constant at every section along the
channel reach.
(2) The total energy line, water surface
and the channel bottom are all parallel,
that is, their slopes are all equal, or
Sf = Sw = S0 = S where Sf is energy line
slope, Sw is water surface slope and S0 is
channel bottom slope.

19. f
h
z
g
V
y
z
g
V
y +
+
+
=
+
+ 2
2
2
2
1
2
1
1
2
2
w
f
f
S
S
L
h
S
L
Z
Z
=
=
=
=
−
0
2
1
Consider a short reach of prismatic channel
having uniform flow. Applying Bernoulli's equation
between sections 1 and 2 at a distance L apart,
where hf is the loss of energy between the two
sections. Since the flow is uniform, y1=y2; V1 = V2.
Thus from the above expression Z1-Z2 =hf
The depth of a uniform flow is called the normal
depth and it is generally represented by yn.

20. In uniform flow since the velocity of flow does not
change along the length of the channel, there is no
acceleration. Hence the sum of the components of
all the external forces in the direction of flow must
be equal to zero.

21. 0
sin 0 =
− 
 PL
wAL 0
0 sin wRS
P
A
w =
= 

S
S =
 
sin
0
According to Newton's second law of motion, in
the direction of flow
or
Where R is the hydraulic radius and
S is the slope of the channel bottom.

22. wRS
V
f
=
= 2
0
8


RS
C
RS
f
g
RS
f
w
V =
=
=
8
8

But when mass density ρ, average velocity and
Darcy’s friction co-efficient f are known
or
The above equation is known as Chezy’s formula
and C is called Chezy’s co-efficient.

23. y
A
B = y
y
A
P 2
+
=
A = B y P = B + 2y
For a rectangular section the c/s area and wetted
perimeter are given by

24. 0
2
2
=
+
−
=
y
A
dy
dP y
B
y
A =
= 2
2
y
B 2
= 2
B
y =
For efficient section, Hydraulic radius,
2
4
2
2
2
2
2
2
2
y
y
y
y
y
y
y
B
By
P
A
R =
=
+
=
+
=
=
For an efficient section,

25. A Trapezoidal section has three dimensions –
bed width B, depth of flow y and side slope z

26. ( )y
zy
B
A +
= 2
1
2 z
y
B
P +
+
=
zy
y
A
B −
=
2
1
2 z
y
zy
y
A
P +
+
−
=
For a Trapezoidal section the c/s area and wetted
perimeter are given by

27. 0
1
2 2
2
=
+
+
−
−
= z
z
y
A
dy
dP
2
2
1
2 z
z
y
A
+
=
+
( ) 2
2
1
2 z
z
y
y
zy
B
+
=
+
+
( ) 2
1
2
2
z
y
zy
B
+
=
+
zy
z
y
B 2
1
2 2
−
+
=
For an efficient section,
or

28. P
A
R =
( )
2
1
2 z
y
B
y
zy
B
+
+
+
=
( )
2
2
2
1
2
2
1
2
2
1
2
z
y
zy
z
y
y
zy
zy
z
y
R
+
+
−
+
+
−
+
=
2
y
R =
Hydraulic radius,
For efficient section,