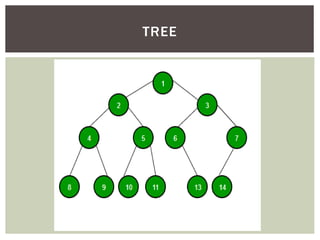
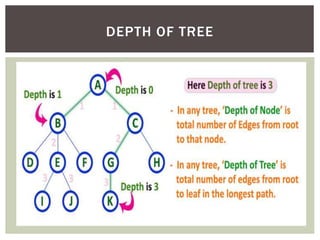
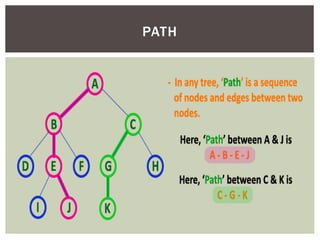
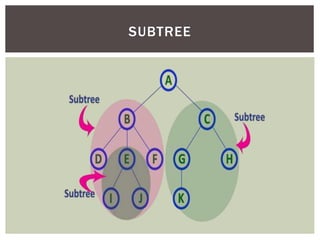
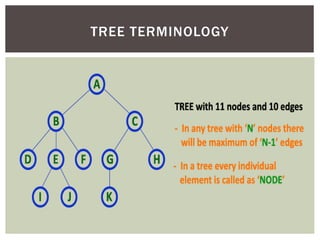
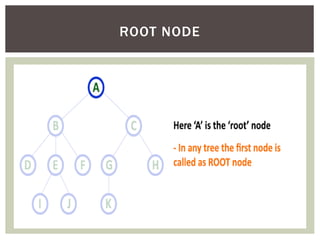
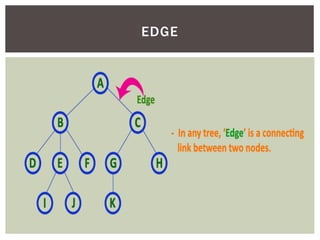
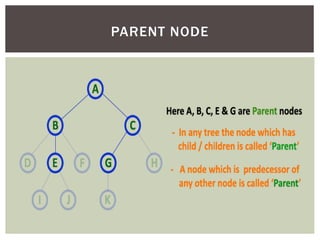
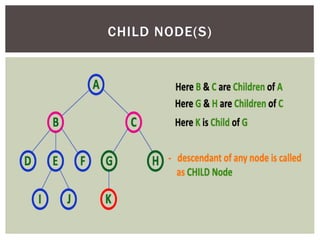
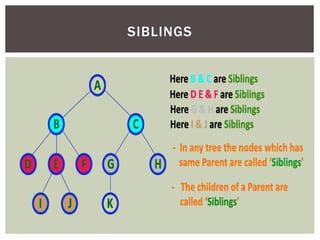
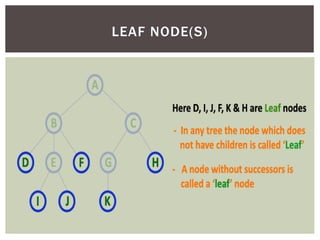
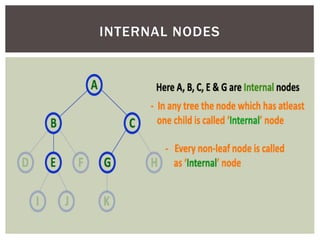
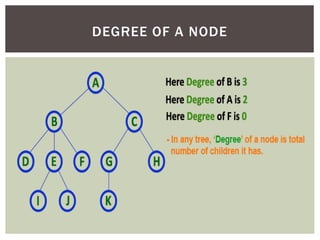
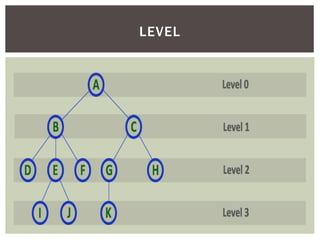
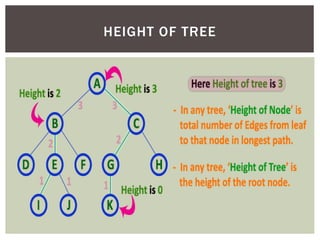
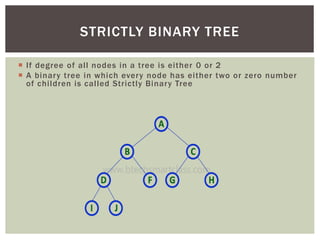
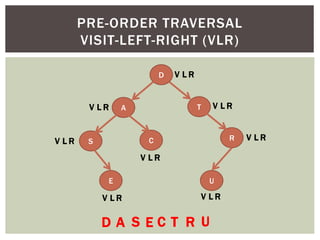
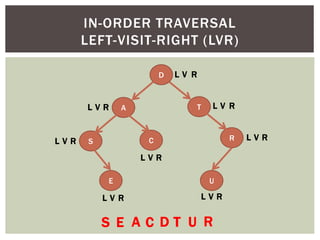
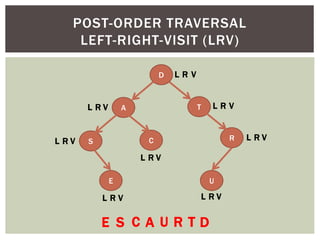
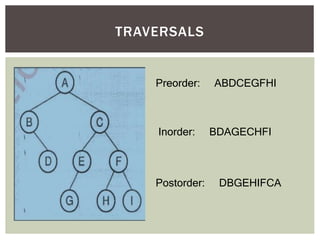
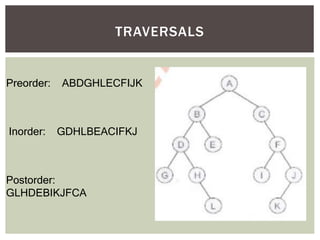
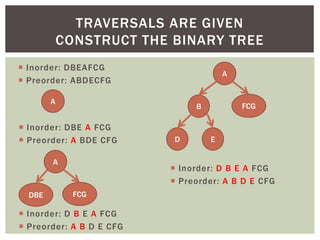
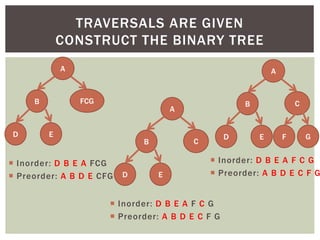
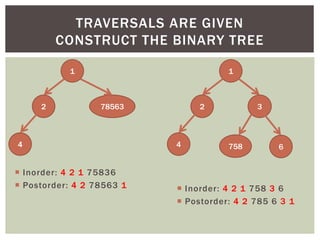
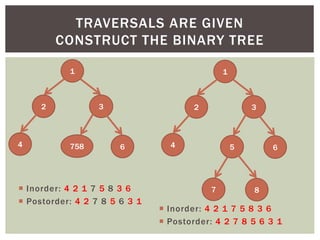
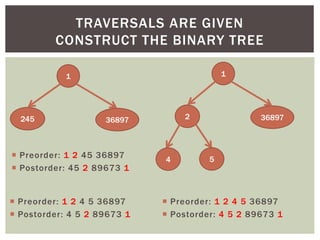
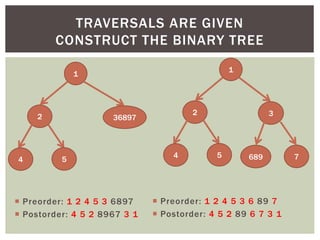
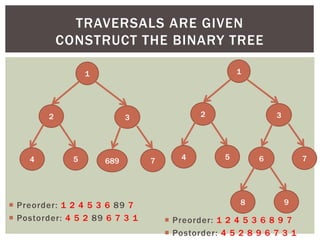
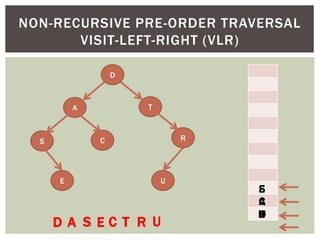
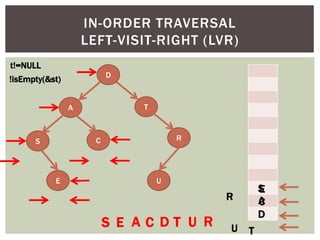
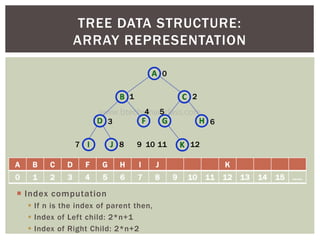
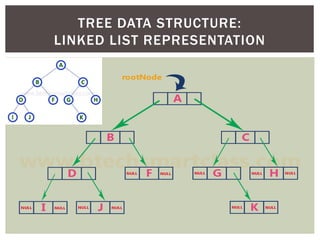
This document discusses various tree data structures and algorithms: - It defines common tree terminology like root, child, leaf nodes. - It describes different types of binary trees like binary, strictly binary, and complete binary trees. - It covers tree traversal algorithms like preorder, inorder and postorder traversals. - It discusses binary tree representations using arrays and linked lists. 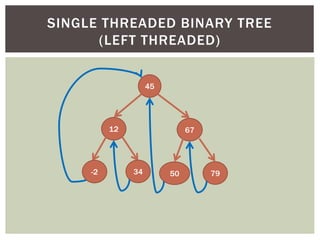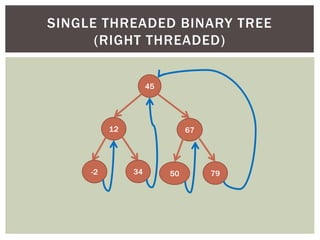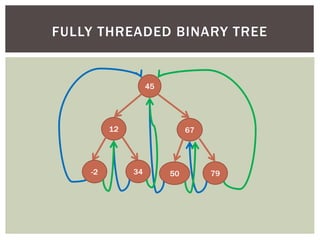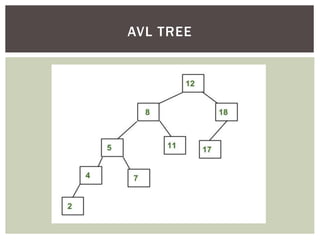- Additional tree topics covered include binary search trees, threaded binary trees, AVL trees, B-trees, and other tree variations.

1. Prof. Sonali
Mhatre
DATA STRUCTURES AND
ANALYSIS

2. TREE

3. TREE

4. TREE TERMINOLOGY

5. ROOT NODE

6. EDGE

7. PARENT NODE

8. CHILD NODE(S)

9. SIBLINGS

10. LEAF NODE(S)

11. INTERNAL NODES

12. DEGREE OF A NODE

13. LEVEL

14. HEIGHT OF TREE

15. DEPTH OF TREE

16. PATH

17. SUBTREE

18.  If degree of all nodes in a tree is either 0, 1 or 2
 A tree in which every node can have a maximum of two
children is called Binary Tree.
BINARY TREE

19.  If degree of all nodes in a tree is either 0 or 2
 A binary tree in which every node has either two or zero number
of children is called Strictly Binary Tree
STRICTLY BINARY TREE

20.  A binary tree in which every internal node has exactly two
children and all leaf nodes are at same level is called Complete
Binary Tree.
 At level L there must be 2L no. of Nodes
COMPLETE BINARY TREE

21.  Array representation
 Linked list representation
BINARY TREE DATA STRUCTURE

22. TREE DATA STRUCTURE:
ARRAY REPRESENTATION
0
1 2
3
4 5
6
7 8 9 10 11 12
A B C D F G H I J K
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 …..
 Index computation
 If n is the index of parent then,
 Index of Left child: 2*n+1
 Index of Right Child: 2*n+2

23. TREE DATA STRUCTURE:
LINKED LIST REPRESENTATION

24.  Visiting order of nodes in a binary tree is called as Binary Tree
Traversal.
 Three traversals
 Pre - Order Traversal (Visit-Left-Right)
 In - Order Traversal (Left-Visit-Right)
 Post - Order Traversal (Left-Right-Visit)
BINARY TREE TRAVERSALS

25. PRE-ORDER TRAVERSAL
VISIT-LEFT-RIGHT (VLR)
D
A T
S C
U
R
E
V L R
D
V L R
A
V L R
S
V L R
E
V L R
V L R
V L R
V L R
C T R U

26. IN-ORDER TRAVERSAL
LEFT-VISIT-RIGHT (LVR)
D
A T
S C
U
R
E
L V R
S
L V R
E
L V R
A
L V R
C
L V R
L V R
L V R
L V R
D T U R

27. POST-ORDER TRAVERSAL
LEFT-RIGHT-VISIT (LRV)
D
A T
S C
U
R
E
L R V
E
L R V
S
L R V
C
L R V
A
L R V
L R V
L R V
L R V
U R T D

28. struct Node
{
int el;
struct Node * left;
struct Node * right;
};
STRUCT NODE

29. struct Node * createNode()
{
struct Node * n=(struct Node *)malloc(sizeof(struct Node));
printf("nEnter Node Value: ");
scanf("%d",&n->el);
n->left=NULL;
n->right=NULL;
return n;
}
MEMORY ALLOCATION FOR NODE

30. struct Node * createTree(struct Node * r)
{
struct Node * t;
int c;
if(r==NULL)
{
r=createNode();
}
TREE CREATION (ROOT NODE)

31. t=r;
printf("n%d has Left Child? ",t->el);
scanf("%d",&c);
if(c==1)
{
t->left=createNode();
t->left=createTree(t->left);
}
printf("n%d has Right Child? ",t->el);
scanf("%d",&c);
if(c==1)
{
t->right=createNode();
t->right=createTree(t->right);
}
return r;
}
TRE CREATION (LEFT & RIGHT SUBTREE)

32. void preOrder(struct Node * t)
{
if(t!=NULL)
{
printf("%d ",t->el);
preOrder(t->left);
preOrder(t->right);
}
}
PREOREDER TRAVERSAL

33. void inOrder(struct Node * t)
{
if(t!=NULL)
{
inOrder(t->left);
printf("%d ",t->el);
inOrder(t->right);
}
}
INORDER TRAVERSAL

34. void postOrder(struct Node * t)
{
if(t!=NULL)
{
postOrder(t->left);
postOrder(t->right);
printf("%d ",t->el);
}
}
POSTORDER TRAVERSAL

35. TRAVERSALS
Preorder: ABDCEGFHI
Inorder: BDAGECHFI
Postorder: DBGEHIFCA

36. TRAVERSALS
Preorder: ABDGHLECFIJK
Inorder: GDHLBEACIFKJ
Postorder:
GLHDEBIKJFCA

37.  Inorder: DBEAFCG
 Preorder: ABDECFG
TRAVERSALS ARE GIVEN
CONSTRUCT THE BINARY TREE
A
 Inorder: DBE A FCG
 Preorder: A BDE CFG
A
DBE
 Inorder: D B E A FCG
 Preorder: A B D E CFG
FCG
A
B FCG
D E
 Inorder: D B E A FCG
 Preorder: A B D E CFG

38. TRAVERSALS ARE GIVEN
CONSTRUCT THE BINARY TREE
A
B FCG
D E
 Inorder: D B E A FCG
 Preorder: A B D E CFG
A
B C
D E
 Inorder: D B E A F C G
 Preorder: A B D E C F G
A
B C
D E F G
 Inorder: D B E A F C G
 Preorder: A B D E C F G

39.  Inorder: 42175836
 Postorder: 42785631
TRAVERSALS ARE GIVEN
CONSTRUCT THE BINARY TREE
1
 Inorder: 42 1 75836
 Postorder: 42 78563 1
1
42 78563
 Inorder: 4 2 1 75836
 Postorder: 4 2 78563 1
1
2 78563
4
 Inorder: 4 2 1 75836
 Postorder: 4 2 78563 1

40. TRAVERSALS ARE GIVEN
CONSTRUCT THE BINARY TREE
1
2 78563
4
 Inorder: 4 2 1 75836
 Postorder: 4 2 78563 1
1
2 3
4
 Inorder: 4 2 1 758 3 6
 Postorder: 4 2 785 6 3 1
758 6

41. 1
2 3
4
 Inorder: 4 2 1 7 5 8 3 6
 Postorder: 4 2 7 8 5 6 3 1
758 6
TRAVERSALS ARE GIVEN
CONSTRUCT THE BINARY TREE
1
2 3
4 5 6
7 8
 Inorder: 4 2 1 7 5 8 3 6
 Postorder: 4 2 7 8 5 6 3 1

42.  Preorder: 124536897
 Postorder: 452896731
TRAVERSALS ARE GIVEN
CONSTRUCT THE BINARY TREE
1
 Preorder: 1 24536897
 Postorder: 45289673 1
 Preorder: 1 245 36897
 Postorder: 452 89673 1
1
245 36897
 Preorder: 1 2 45 36897
 Postorder: 45 2 89673 1

43. TRAVERSALS ARE GIVEN
CONSTRUCT THE BINARY TREE
1
245 36897
 Preorder: 1 2 45 36897
 Postorder: 45 2 89673 1
 Preorder: 1 2 4 5 36897
 Postorder: 4 5 2 89673 1
1
2 36897
4 5
 Preorder: 1 2 4 5 36897
 Postorder: 4 5 2 89673 1

44. 1
2 36897
4 5
 Preorder: 1 2 4 5 3 6897
 Postorder: 4 5 2 8967 3 1
TRAVERSALS ARE GIVEN
CONSTRUCT THE BINARY TREE
1
2 3
4 5
 Preorder: 1 2 4 5 3 6 89 7
 Postorder: 4 5 2 89 6 7 3 1
689 7

45. TRAVERSALS ARE GIVEN
CONSTRUCT THE BINARY TREE
1
2 3
4 5
 Preorder: 1 2 4 5 3 6 89 7
 Postorder: 4 5 2 89 6 7 3 1
689 7
1
2 3
4 5 6 7
8 9
 Preorder: 1 2 4 5 3 6 8 9 7
 Postorder: 4 5 2 8 9 6 7 3 1

46.  Preorder: 1234
 Postorder: 4321
TRAVERSALS ARE GIVEN
CONSTRUCT THE BINARY TREE
1
 Preorder: 1 2 34
 Postorder: 43 2 1
1
234
 Preorder: 1 234
 Postorder: 432 1
1
2
34
 Preorder: 1 2 3 4
 Postorder: 4 3 2 1 1
2
3
4
2
3
4

47.  Unique Binary Tree can be constructed from
 Inorder and Preorder sequences
 Inorder and Postorder sequences
 But Preorder and Postorder sequences do not guarantee
construction of Unique Binary Tree.
ANALYSIS

48.  Recursive traversals make implicit use of Stack
 Non-Recursive traversals make explicit use of Stack
NON RECURSIVE TRAVERSAL

49. NON-RECURSIVE PRE-ORDER TRAVERSAL
VISIT-LEFT-RIGHT (VLR)
D
A T
S C
U
R
E
D A S E C T R U
D
T
A
C
S
E
R
U

50. push(&st,t);
while(!isEmpty(&st))
{
n=pop(&st);
printf("%d ",n->el);
if(n->right!=NULL)
push(&st,n->right);
if(n->left!=NULL)
push(&st,n->left);
}
NON-RECURSIVE PRE-ORDER TRAVERSAL
VISIT-LEFT-RIGHT (VLR)

51. IN-ORDER TRAVERSAL
LEFT-VISIT-RIGHT (LVR)
D
A T
S C
U
R
E
S E A C D T U R
D
T
A
C
S
E
R
U
t!=NULL
!isEmpty(&st)

52. while(t!=NULL || !isEmpty(&st))
{
if(t!=NULL)
{
push(&st,t);
t=t->left;
}
else
{
t=pop(&st);
printf("%d ",t->el);
t=t->right;
}
}
NON-RECURSIVE IN-ORDER TRAVERSAL
LEFT-VISIT-RIGHT (LVR)

53. push(&st,t);
while(!isEmpty(&st))
{
n=peek(&st);
if(pn==NULL || pn->left==n || pn->right==n)
{
if(n->left!=NULL)
push(&st,n->left);
else if(n->right!=NULL)
push(&st,n->right);
else
{
printf("%d ",n->el);
pop(&st);
}
}
NON-RECURSIVE POST-ORDER TRAVERSAL
LEFT-RIGHT-VISIT (LRV)

54. if(pn==n->left)
{
if(n->right!=NULL)
push(&st,n->right);
else
{
printf("%d ",n->el);
pop(&st);
}
}
if(pn==n->right)
{
printf("%d ",n->el);
pop(&st);
}
pn=n;
}
NON-RECURSIVE POST-ORDER TRAVERSAL
LEFT-RIGHT-VISIT (LRV)

55.  For all Internal Nodes
 Value of Left child node is less than the value of all its ancestors
 Value of Right child node is greater than the value of all its ancestors
BINARY SEARCH TREE (BST)
45
12 67
-2 34 50 79

56.  In-order traversal of BST is a sorted list of elements in
ascending order
BINARY SEARCH TREE (BST)
 Pre-order: 45 12 -2 34 67 50 79
 In-order: -2 12 34 45 67 50 79
 Post-order: -2 34 12 50 79 67 45

57.  Empty NULL pointers are used as threads
 Threaded Binary Tree
 Single Threaded
 Left threaded
 Right threaded
 Fully threaded
 In the left threaded mode if some node has no left child, then
the left pointer will point to its inorder predecessor
 In the right threaded mode if some node has no right child,
then the right pointer will point to its inorder successor I
 If no successor or predecessor is present, then it will point to
header node.
THREADED BINARY TREE

58. 45
12 67
-2 34 50 79
SINGLE THREADED BINARY TREE
(LEFT THREADED)

59. 45
12 67
-2 34 50 79
SINGLE THREADED BINARY TREE
(RIGHT THREADED)

60. 45
12 67
-2 34 50 79
FULLY THREADED BINARY TREE

61.  Adelson, Velski & Landis
 AVL trees are height balancing binary search tree.
 The difference between heights of left and right subtrees
cannot be more than one for all nodes.
AVL TREE

62. AVL TREE

63.  Binary search tree: Traversal, searching, insertion and
deletion in binary search tree. Threaded Binary Tree: Finding
in-order successor and predecessor of a node in threaded
tree. Insertion and deletion in threaded binary tree. AVL Tree:
Searching and traversing in AVL trees. Tree Rotations: Right
Rotation, Left Rotation. Insertion and Deletion in an AVL Tree.
 B-tree: Searching, Insertion, Deletion from leaf node and non-
leaf node.
 B+ Tree, Digital Search Tree, Game Tree & Decision Tree