Springer base paper

Progressive medical image coding using
binary wavelet transforms

Tirupathiraju Kanumuri, M. L. Dewal &
R. S. Anand

Signal, Image and Video Processing

ISSN 1863-1703

SIViP
DOI 10.1007/s11760-012-0325-1

1 23

Your article is protected by copyright and all
rights are held exclusively by Springer-Verlag
London Limited. This e-offprint is for personal
use only and shall not be self-archived in
electronic repositories. If you wish to self-
archive your work, please use the accepted
author’s version for posting to your own
website or your institution’s repository. You
may further deposit the accepted author’s
version on a funder’s repository at a funder’s
request, provided it is not made publicly
available until 12 months after publication.

1 23

Author's personal copy
SIViP
DOI 10.1007/s11760-012-0325-1

ORIGINAL PAPER

Progressive medical image coding using binary wavelet transforms
Tirupathiraju Kanumuri · M. L. Dewal · R. S. Anand

Received: 25 September 2011 / Revised: 21 April 2012 / Accepted: 23 April 2012
© Springer-Verlag London Limited 2012

Abstract In this paper, a new algorithm for progressive transmission. In telemedicine, the medical images are trans-
medical image coding is presented. An 8-bit gray scale mitted over long distances through Internet. This is mainly
image is divided into eight binary bit-planes, and then, binary used in remote places such as villages, ships and air planes
wavelet transform is performed on each bit-plane to extract where the specialized doctor is not available for diagnosis.
the three-level multi-resolution binary wavelet transformed As the communication channel in such places is very narrow,
images. Starting from the most significant bit-plane, each bit- embedded image coding method that can provide progressive
plane is encoded using quadtree-based partitioning scheme to reconstruction is preferred so that the doctor can stop decod-
exploit the energy concentration in the high-frequency sub- ing based on the individual requirements at the decoding
bands. Experiments are conducted on ultrasound, MRI and end. In this paper, a new method is proposed for progressive
CT images to prove the effectiveness of the proposed algo- coding of medical images. The previously available progres-
rithm. The results show a significant improvement in terms sive image coding methods can be classified into three cat-
of bit-rate for the required peak signal-to-noise ratio and cor- egories: spatial domain methods [1–6], pyramidal structure
relation coefficient as compared to the existing state-of-art methods [7–10] and transform domain methods [11–27]. Out
progressive image coding methods. of the available techniques, transform domain techniques are
more efficient due to their compression efficiency and hence
Keywords Binary wavelet transforms (BWT) · Progressive employed in JPEG and JPEG 2000 image coding standards
image coding · Medical image compression [11,16].
A progressive coding method based on prioritized coding
of DCT coefficients is proposed in [11]. DCT suffers from
1 Introduction blocking artifacts for low bit-rates, and to avoid this, many
wavelets-based embedded image coding methods are pro-
With the advent development of digital imaging and image posed. Shapiro [12] introduced lossy to lossless progressive
processing technology, all the hospitals are moving toward embedded image coding method, embedded zerotree wave-
digitization of medical images for processing, storage and let coding (EZW). Further, Zandi et al. extended the EZW
transmission purposes. This requires huge amount of stor- with the reversible wavelets (CREW) [13]. Said and Pearl-
age space for data storage and higher band width for image man introduced an algorithm known as set partitioning in
hierarchical trees (SPIHT) [14] which utilizes the concept
of parent–child relationship across wavelet subbands. Fur-
T. Kanumuri (B) · M. L. Dewal · R. S. Anand
ther, Pearlman and Asad have extended the SPIHT, set par-
Department of Electrical Engineering, Indian Institute of Technology,
Roorkee, Roorkee, 247667 Uttarakhand, India titioning embedded block coder (SPECK) [15] that exploits
e-mail: ktrajuiitr@gmail.com the parent–child relationship as well as clustering of energy
M. L. Dewal in the frequency domain. Taubman proposed a block-based
e-mail: mohanfee@iitr.ernet.in coding method, embedded block coding with optimized trun-
R. S. Anand cation of the embedded bit-streams (EBCOT) [16], and it is
e-mail: anandfee@iitr.ernet.in included in JPEG 2000. Pan and Siu introduced progressive

123

SIViP

partitioning binary wavelet tree coder (PPBWC) [17] using ¯
a|s=k defines a vector with elements formed from a circular
binary wavelet transforms (BWT). They have combined the ¯
shifted sequence of a by k. and
features of zigzag scanning in EZW [12] and partitioning
a = {a0 , a1 , . . . , a S−1 }T
¯
priority coding of progressive DCT [11] to encode the BWT. (3)
A concise review of the available related literature, tar- ¯
d = {d0 , d1 , . . . , d S−1 }T
geted for development of our algorithm, is presented. Binary
where S is the number of scales, ai and di are the approximate
wavelet transform (BWT) is first proposed for binary image
(lowpass) and detail (highpass) coefficients, respectively.
compression [17–22]. Later, it has been extended to gray
The BWT is then defined [23] as:
scale image by separating the gray scale image into series of
binary bit-planes, and then, the BWT is performed on each y = Wx (4)
bit-plane [23]. Law and Sui proposed the in-place implemen-
tation for BWT [17] using lifting scheme that is similar to Law and Sui proposed the in-place implementation for BWT
the lifting scheme in the real wavelet transform. BWT has [17]. The 32 length-8 binary filters are classified into four
several advantages over the bi-orthogonal wavelets [25] and groups depending on the number of ‘1’s in the binary fil-
integer wavelets [26], such as only basic Boolean operations ters. Examples of the binary filters in each group are given
are involved, no quantization during transformation, no need in Table 1. In the proposed method, filters of group 1 are
to transmit the sign bit and the transformed image have the used because the entropy of the transformed image is less
same number of gray levels as the original image. compared to other filters and hence more suitable for image
In BWT, the energy clusters in the transformed subbands compression.
correspond to the spatial locations associated with edges in In order to have an in-place implementation structure, the
the original image. So, the energy is mainly concentrated odd number and even number samples of the original signal
in high-frequency subbands and the parent–child relation- are split into two sequences. These two sequences are then
ship is very weak [17]. So, the state-of-art progressive cod- updated according to the filter coefficients from the low pass
ing methods SPIHT and SPECK are not efficient for binary and high pass filters. The low pass and the high pass outputs
image coding. In this paper, a new coding method is pro- are then interleaved together to get the transformed output.
posed, which uses the energy concentration property of BWT The scheme is depicted in Fig. 1. If length of the input signal
in high-frequency subband. is odd, the last sample is separated out and BWT is applied
The paper is organized as follows: a concise review and for remaining signal and the last sample is added at the end
implementation of 1-D and 2-D BWT is discussed in Sect. 2. of low pass output. For example, if the input signal is of
The Sect. 3 presents the proposed method for encoding 2-D 15 bits length, the low pass filter will have 8 samples and
BWT coefficients. The decoding process is given in Sect. 4. high pass filter will have 7 samples. To go for the next level
The experimental results in support of the proposed algo- decomposition, BWT is applied to the lowpass output.
rithm are discussed in Sect. 5. Finally, the proposed work is
concluded in Sect. 6. 2.2 2-D binary wavelet transform (2-D BWT)

A separable 2-D BWT [28] can be computed efficiently in
binary space by applying the associated one-level 1-D fil-
2 Binary wavelet transform ter bank to each row of the input binary image and to each
column of the resultant low pass and high pass output coef-
2.1 1-D binary wavelet transform (1-D BWT) ficients as shown in Fig. 2. This can be extended to gray
scale image by separating it into binary bit-planes, and then
The BWT is implemented on binary images in the similar performing the BWT to each individual bit-plane of image
manner to the lifting scheme for real wavelet transforms on as shown in Fig. 2. To go for second-level decomposition,
gray scale images [17]. the 2-D BWT is applied to the LL subband.
Let x be an 1 × N signal, the transformed BWT coeffi-
cients matrix W can be constructed as follows
Table 1 Length-8 binary wavelet filters
W = [AD] T
(1) Group Lowpass filter Highpass filter

1 {1, 0, 0, 0, 0, 0, 0, 0} {1, 1, 0, 0, 0, 0, 0, 0}
where
2 {1, 1, 1, 0, 0, 0, 0, 0} {1, 1, 0, 0, 0, 0, 0, 0}
A = (a|s=0 , a|s=2 , . . . , a|s=N −2 )
¯ ¯ ¯ T 3 {1, 1, 1, 1, 0, 0, 0, 1} {1, 1, 0, 0, 0, 0, 0, 0}
(2) 4 {1, 1, 1, 1, 1, 1, 1, 0} {1, 1, 0, 0, 0, 0, 0, 0}
¯ ¯ ¯
D = (d|s=0 , d|s=2 , . . . , d|s=N −2 )T

123

SIViP

3 The proposed encoder subbands by considering them as parents and then go for
the high-frequency subbands. SPECK [15] uses block-based
In real and integer wavelet transforms, the energy is concen- coding by checking low-frequency subbands first, and then,
trated in low-frequency subbands and a parent–child relation- it checks the high-frequency subbands. The energy clusters
ship exists. So, SPIHT [14] starts from the low-frequency in the binary transform subbands correspond to the spatial
locations associated with edges in the original image. So, the
energy is mainly concentrated in high-frequency subbands.
In the proposed method, higher priority is given for encoding
high-frequency subbands than the low-frequency subbands.
In PPBWC [17], each pixel is checked for significance in
every loop until it becomes significant. In case of ultrasound
images, most of the pixels have very low values, and thus, it
necessitates transmitting more bits for checking the signifi-
cance alone. Thus, it is not efficient. In the proposed method,
block-based coding is used, which requires only 4 bits to
be transmitted if the entire bit-plane is zero. In the proposed
method, more emphasis is given for checking high-frequency
subbands to exploit energy concentration.
The flow chart of the proposed method is given in Fig 3.
The input gray scale image is first decomposed into binary
bit-planes, and then, three-level 2-D BWT is calculated for
each bit-plane starting from the most significant bit-plane
(MSB) to the least significant bit-plane (LSB). Initially, the
binary wavelet transformed image of each bit-plane is divided
Fig. 1 In-place implementation of 1-D BWT for one level into 4 blocks as shown in Fig. 4. To give higher priority for

Fig. 2 One-level 2-D BWT implementation for one bit-plane of gray scale image

123

SIViP

Fig. 3 Flow chart of the
proposed encoder

Fig. 4 Quadtree partitioning of
transformed binary image

encoding high-frequency subbands, HH1 is taken as B1 , LH1 and each of the blocks is checked for significance. As each
is taken as B2 , HL1 is taken as B3 , and the remaining block time 4 blocks are checked for significance, each 4 bits of the
is taken as B4 . output are combined together and converted to the decimal
The significance of the block B is checked by form. After completely processing each bit-plane, output is
encoded using Huffman coding. Now, it moves on to the next
1, i f max |ci, j | = 1
τn (B) = (i, j)∈B (5) bit-plane and undergoes the same process. As the proposed
0, else method involves only simple checking and division opera-
tions, it is easy to implement.
where ci, j is transformed coefﬁcient at pixel location (i, j)
B1 , B2 , B3 and B4 are checked for significance in serial
order using Eq. (5). If Bi (i = 1 : 4) is not significant, 0
is added to output and further processing of Bi is discarded, 4 Decoding process
and it goes for the next block. If it is significant, 1 is added
to output to indicate to the decoder that it is significant and The data are received from MSB bit-plane to LSB bit-plane.
it is decomposed into four equal parts as shown in Fig. 5, User can stop decoding after any bit-plane when the required

123

SIViP

Table 2 Length-8 inverse binary wavelet filters
Group Lowpass filter Highpass filter

1 {1, 1, 0, 0, 0, 0, 0, 0} {0, 1, 0, 0, 0, 0, 0, 0}
2 {0, 0, 1, 1, 0, 0, 0, 0} {0, 1, 1, 1, 0, 0, 0, 0}
3 {0, 0, 0, 0, 0,0, 1, 1} {1, 0, 0, 0, 1, 1, 1, 1}
4 {0, 0, 0, 0, 0,0, 1, 1} {0, 1, 1, 1, 1, 1, 1, 1}
Fig. 5 Quadtree partitioning of B

sponding block in the original image. For example, if the
clarity is reached. The flow chart for the decoder of the
image size is 512 × 512, we keep B1 = (257, 257, 256),
proposed method is shown in Fig. 6. The flow chart being
B2 = (257, 1, 256), B3 = (1, 257, 256), B4 = (1, 1, 256).
self-explanatory, the procedure is explained briefly. For each
If the value of OUT(O) is 0, keep all the pixels of block as
loop (bit-plane), apply Huffman decoding and then convert
zeros, increment the value of O by one and go to next block.
each decimal value to 4 bit binary and keep in variable OUT.
Else, divide the block into 4 blocks, increment the value of
Initialize O to 1. Divide the current bit-plane of image into
O by one and check each block for significance as shown in
4 blocks B1, B2, B3, and B4 that is, we keep the starting
pr ocess B(). For example, if we are processing B1, the new
pixel location and size of each block to locate the corre-
blocks will be B1 = (129, 129, 128), B2 = (129, 1, 128),

Fig. 6 flow chart for the
decoder of the proposed method

123

SIViP

Fig. 7 The output of EBCOT
method after each loop for
ultrasound image

Fig. 8 The output of SPIHT
ultrasound image

123

SIViP

Fig. 9 The output of SPECK
ultrasound image

Fig. 10 The output of PPBWC
ultrasound image

123

SIViP

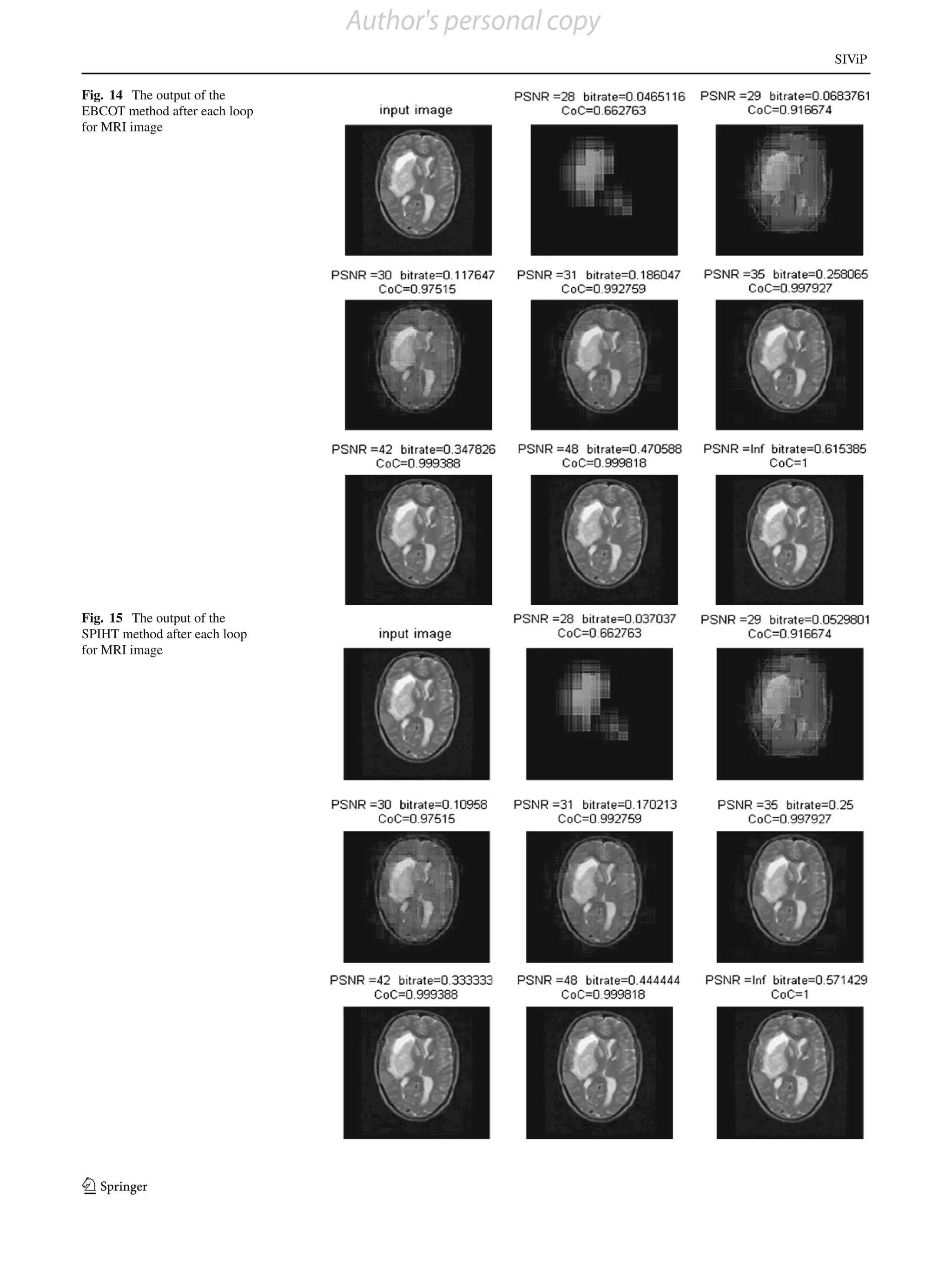
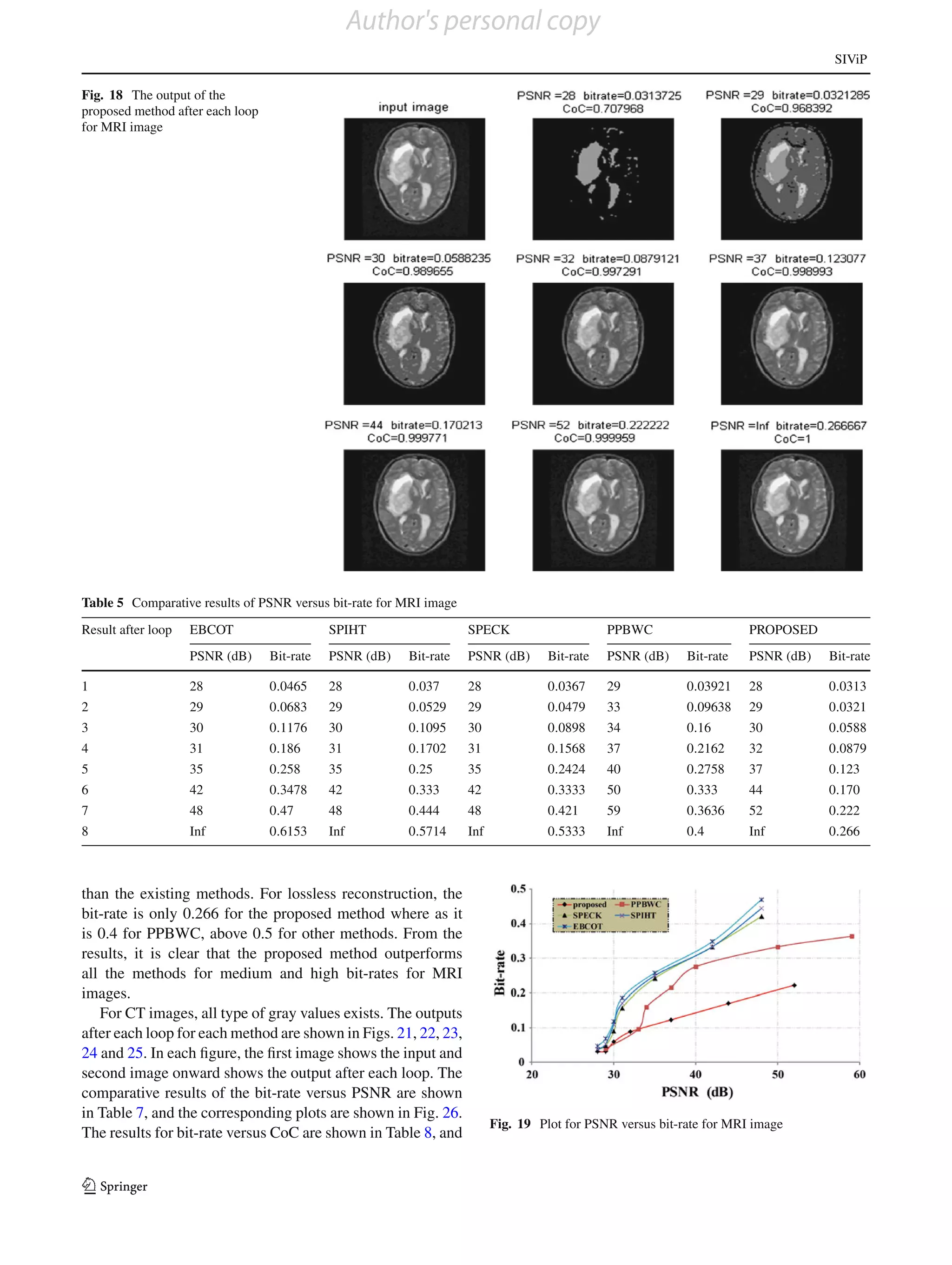
Fig. 11 The output of the
proposed method after each loop
for ultrasound image

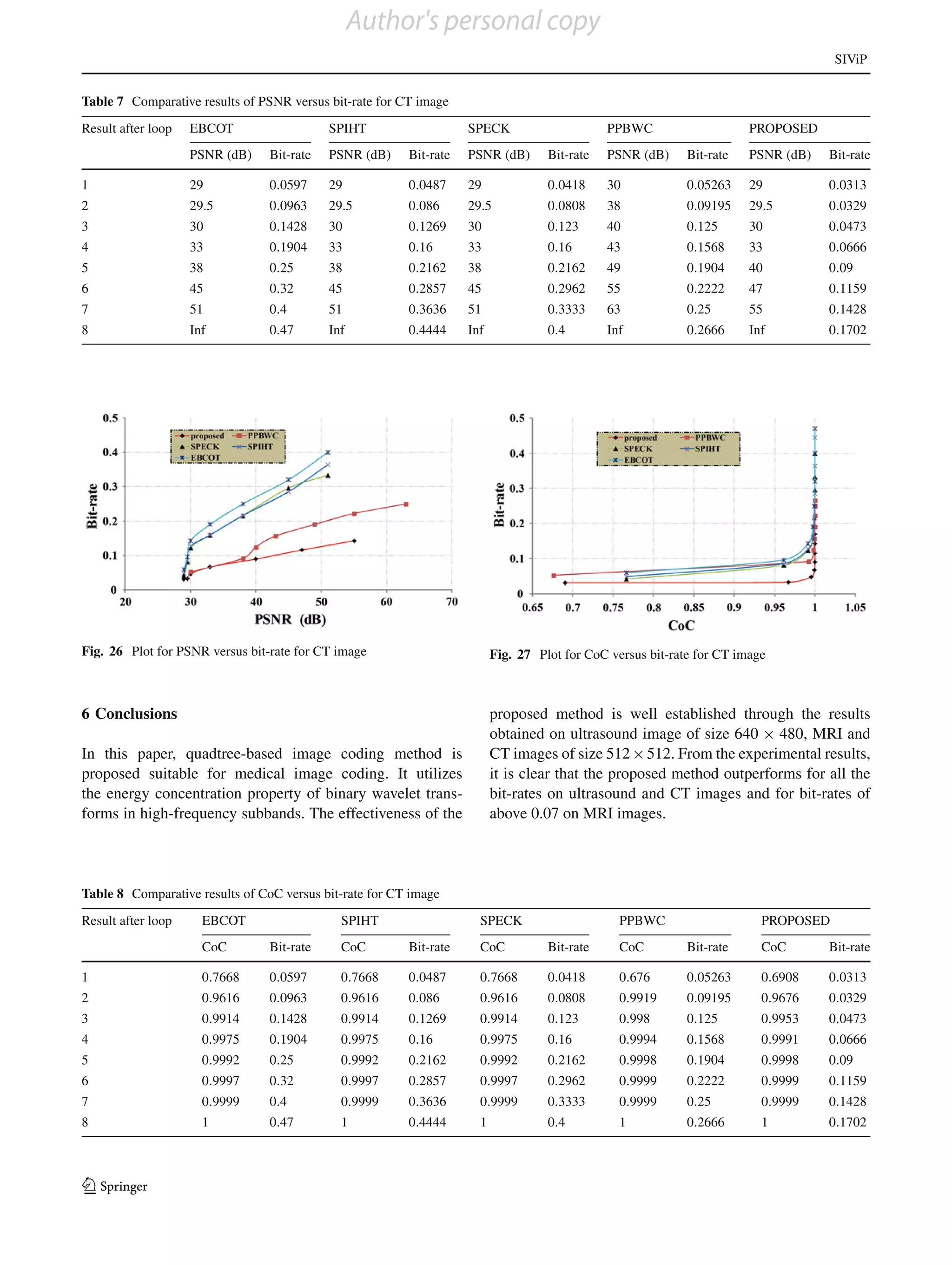
Table 3 Comparative results of PSNR versus bit-rate for ultrasound image
Result after loop EBCOT SPIHT SPECK PPBWC PROPOSED
PSNR (dB) Bit-rate PSNR (dB) Bit-rate PSNR (dB) Bit-rate PSNR (dB) Bit-rate PSNR (dB) Bit-rate

1 27 0.0465 27 0.0313 27 0.0313 27 0.03636 27 0.0313
2 28 0.0720 28 0.0571 28 0.057 29 0.1194 28 0.0792
3 28.5 0.125 28.5 0.1212 28.5 0.1066 31 0.2 32 0.1212
4 30 0.21 30 0.2 30 0.2 38 0.2758 38 0.1632
5 35 0.32 35 0.3076 35 0.32 46 0.32 45 0.2051
6 42 0.42 42 0.4210 42 0.4 55 0.3636 54 0.25
7 48 0.53 48 0.533 48 0.5 64 0.3809 Inf 0.2962
8 Inf 0.666 Inf 0.6153 Inf 0.6153 Inf 0.3892

B3 = (1, 129, 128), B4 = (1, 1, 128). While processing a 5 Experimental results and discussions
block if it is reached to single pixel and value of OUT(O)
is 1, then replace that pixel value in the current bit-plane of The performance of the proposed method is evaluated using
the image with 1. After completing the decoding of the entire the bit-rate for the given peak signal-to-noise ratio (PSNR)
bit-plane, apply three-level inverse BWT and combine all the and the correlation coefficient (CoC) [27]. A set of ten MRI,
bit-planes to form gray scale image. Examples of the inverse ten CT images and five ultrasound images are taken for our
binary filters in each group are given in Table 2. Now check experiment. The proposed method is compared with the state-
whether the required clarity is reached. If it has not reached, of-art progressive image coders. SPIHT [14], SPECK [15]
go for the next loop. and EBCOT [16] are implemented using (2, 2) integer wave-

123

SIViP

Fig. 12 Plot for PSNR versus bit-rate for ultrasound image Fig. 13 Plot for bit-rate versus CoC for ultrasound image

let transforms, and the PPBWC [17] is implemented using decoding after any loop depending on the clarity required for
BWT. We got almost similar results for all the images of each making the diagnosis. For lossless reconstruction, the bit-rate
set, and hence, the results for one image from each group are required for the proposed method is only 0.2962 where as it
presented in this section. is 0.3892 for PPBWC and is above 0.6 for the other methods.
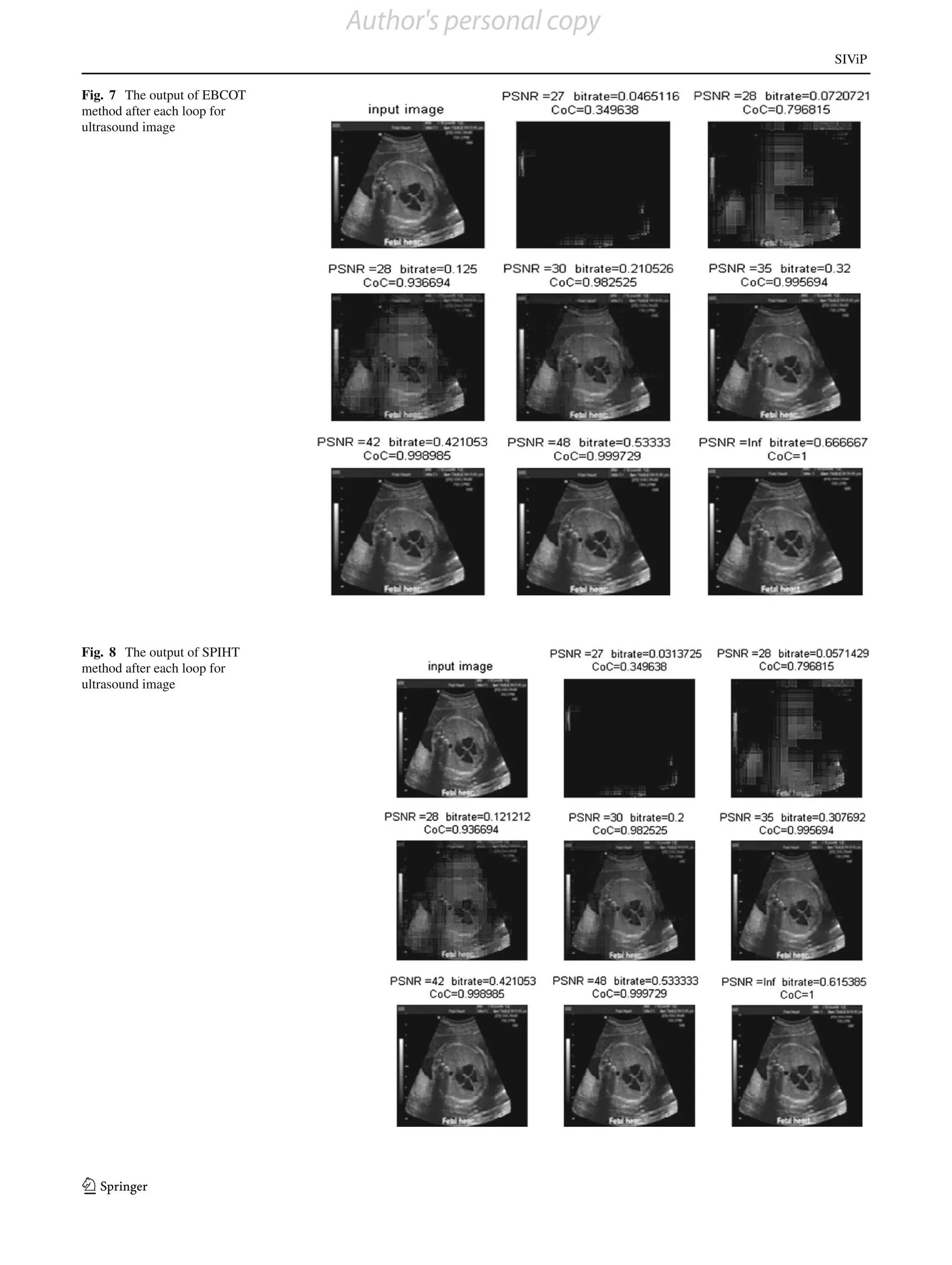
For ultrasound images, most of the pixels’ gray levels are From the results and above observations, it is cleared that the
near to zero. Hence, most of the bit-planes consist of only proposed method outperforms all the methods on ultrasound
zeros, and they need not be encoded. In the proposed method, images.
only four bits are transmitted if all the pixels in the bit-plane For MRI images, most of the pixels’ gray levels have
are zero. But, in PPBWC and SPIHT, more bits are to be medium values. Hence, the proposed method needs more
transmitted. Thus, the proposed method requires lesser bit- bits initially giving inferior results for low bit-rate trans-
rate for the required PSNR and CoC. The outputs after each mission. But, for medium and high bit-rates, the proposed
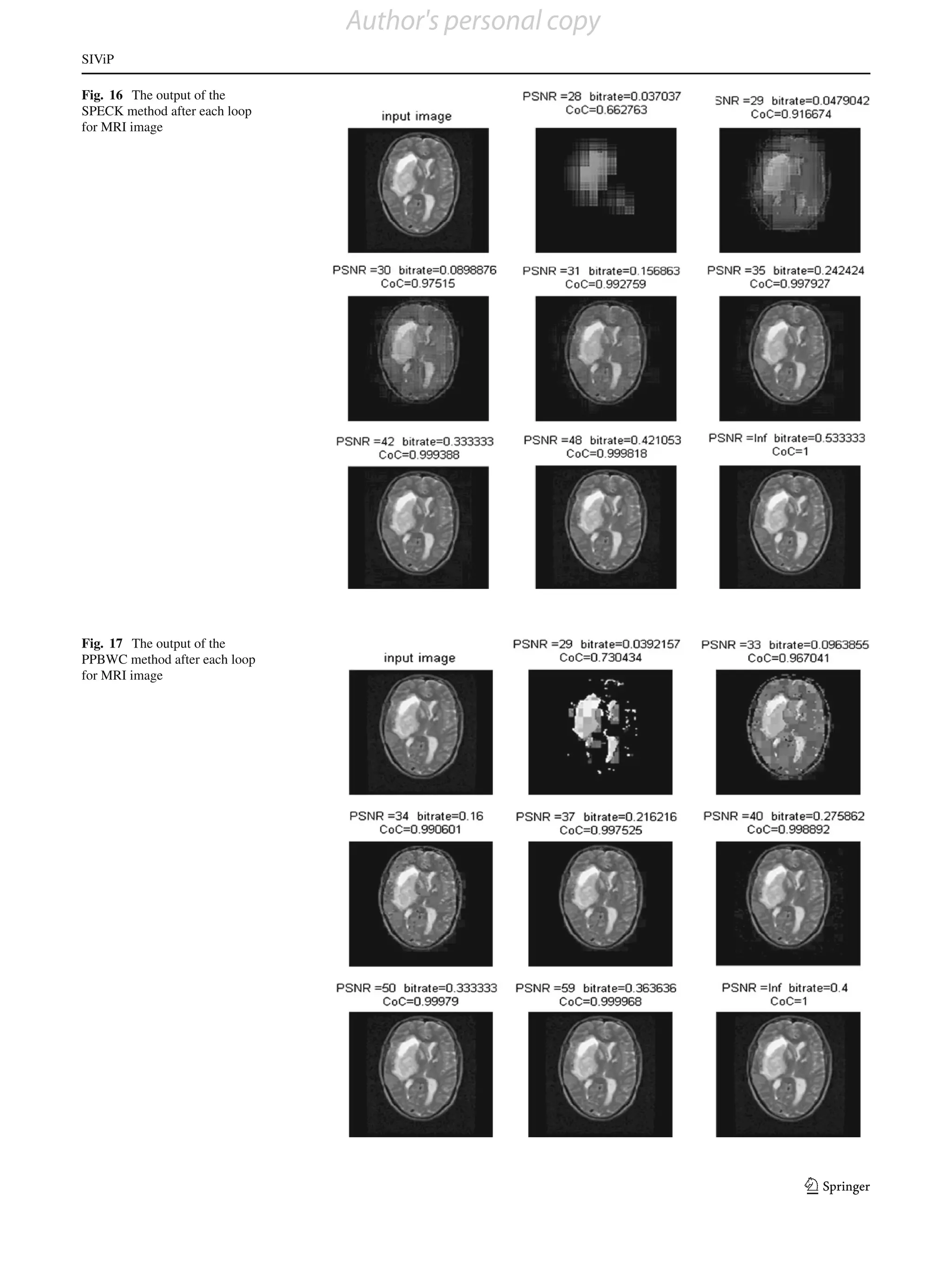
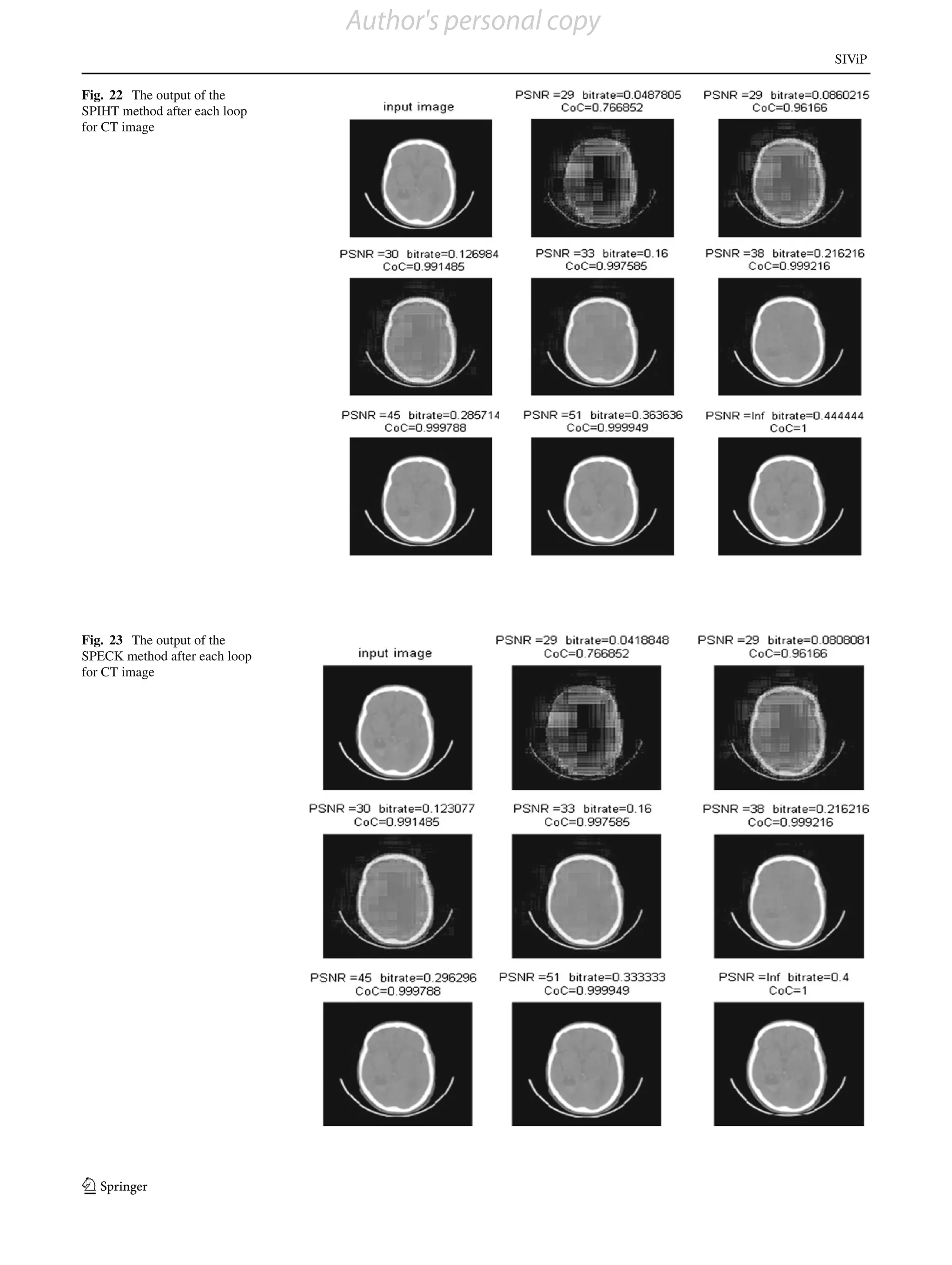
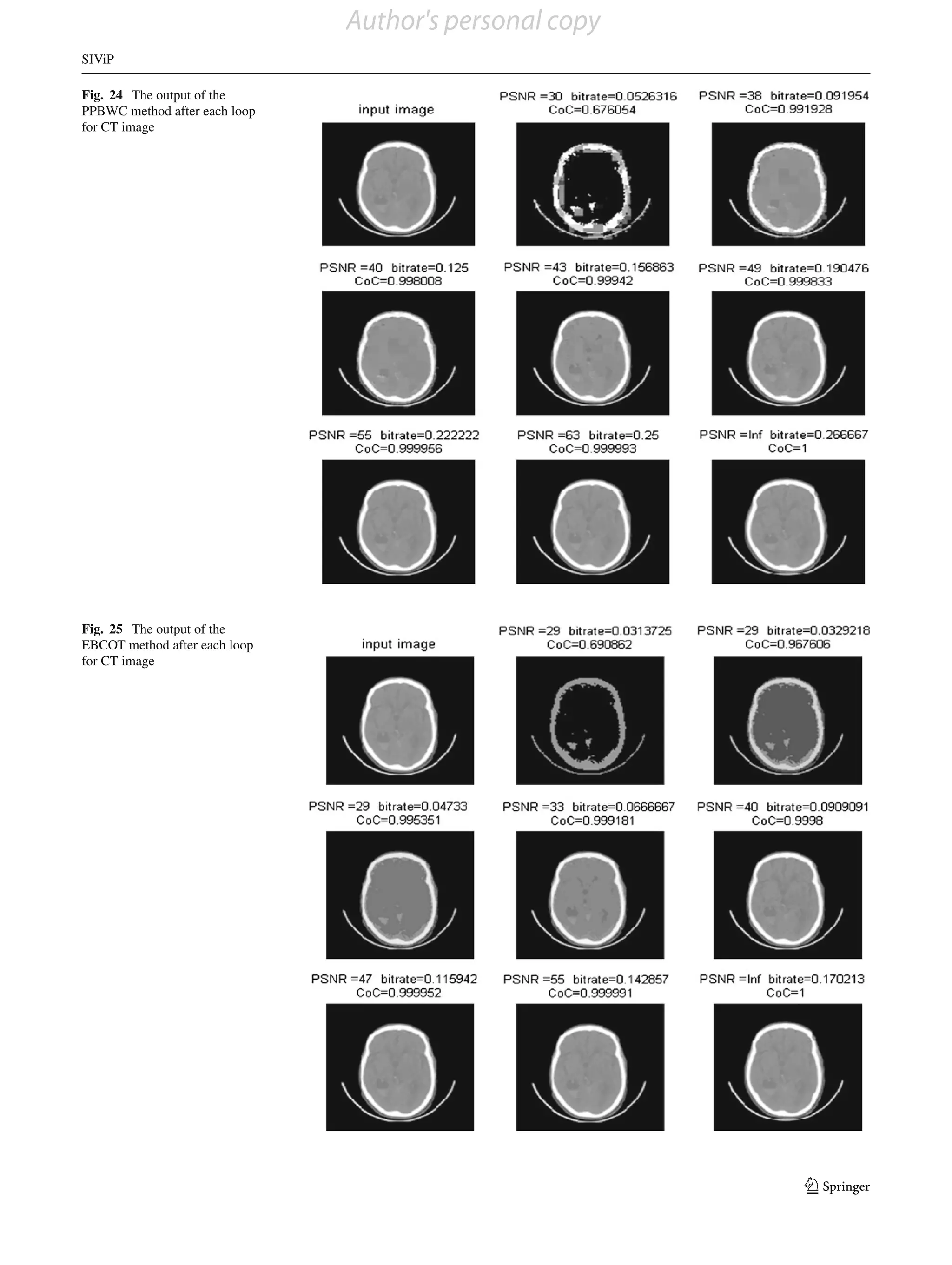
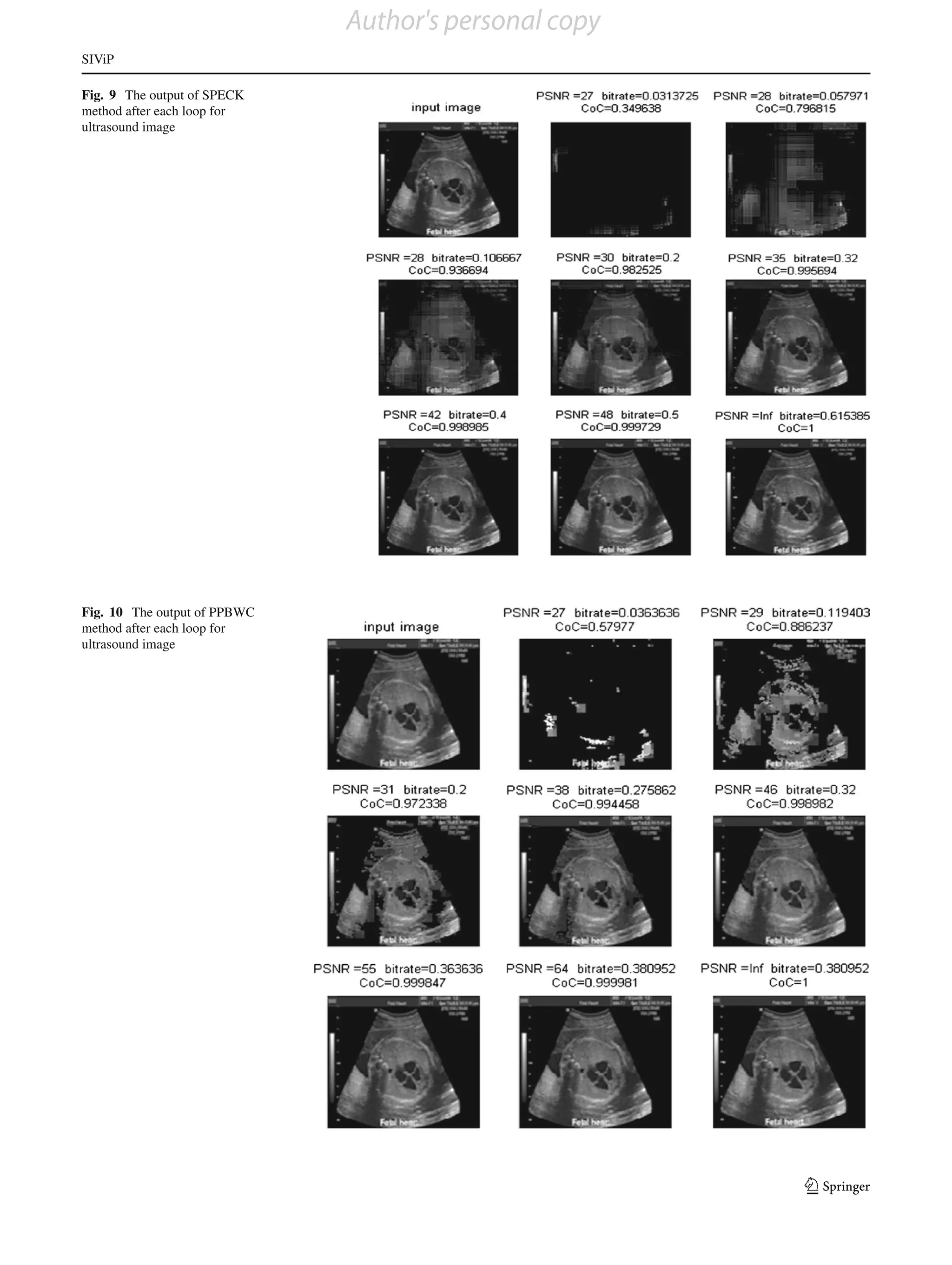
loop for each method are shown in Figs. 7, 8, 9, 10 and 11. method gives better results than existing methods. The out-
In each figure, the first image shows the input and second puts after each loop for each method are shown in Figs. 14,
image onward shows the output after each loop. The com- 15, 16, 17 and 18. In each figure, the first image shows the
parative results of the bit-rate versus PSNR after each loop input and second image onward shows the output after each
for one image are shown in Table 3, and the corresponding loop. The comparative results of the bit-rate versus PSNR
plots are shown in Fig. 12. The results for bit-rate versus CoC are shown in Table 5, and the corresponding plots are shown
after each loop are shown in Table 4, and the corresponding in Fig. 19. The results for bit-rate versus CoC are shown in
plots are shown in Fig. 13. From the plot, it can be seen that Table 6, and the corresponding plots are shown in Fig. 20.
up to 2nd loop, the proposed method is giving comparable From the plots, it can be seen that for a PSNR of 33 and
results and from the 3rd loop onwards, requires very less CoC of 0.96, the PPBWC is giving better results than the
bit-rate when compared with bit-rates obtainable from other proposed method and for PSNR of above 33 and CoC of
methods for the required PSNR and CoC. The user can stop above 0.96, the proposed method is giving better results

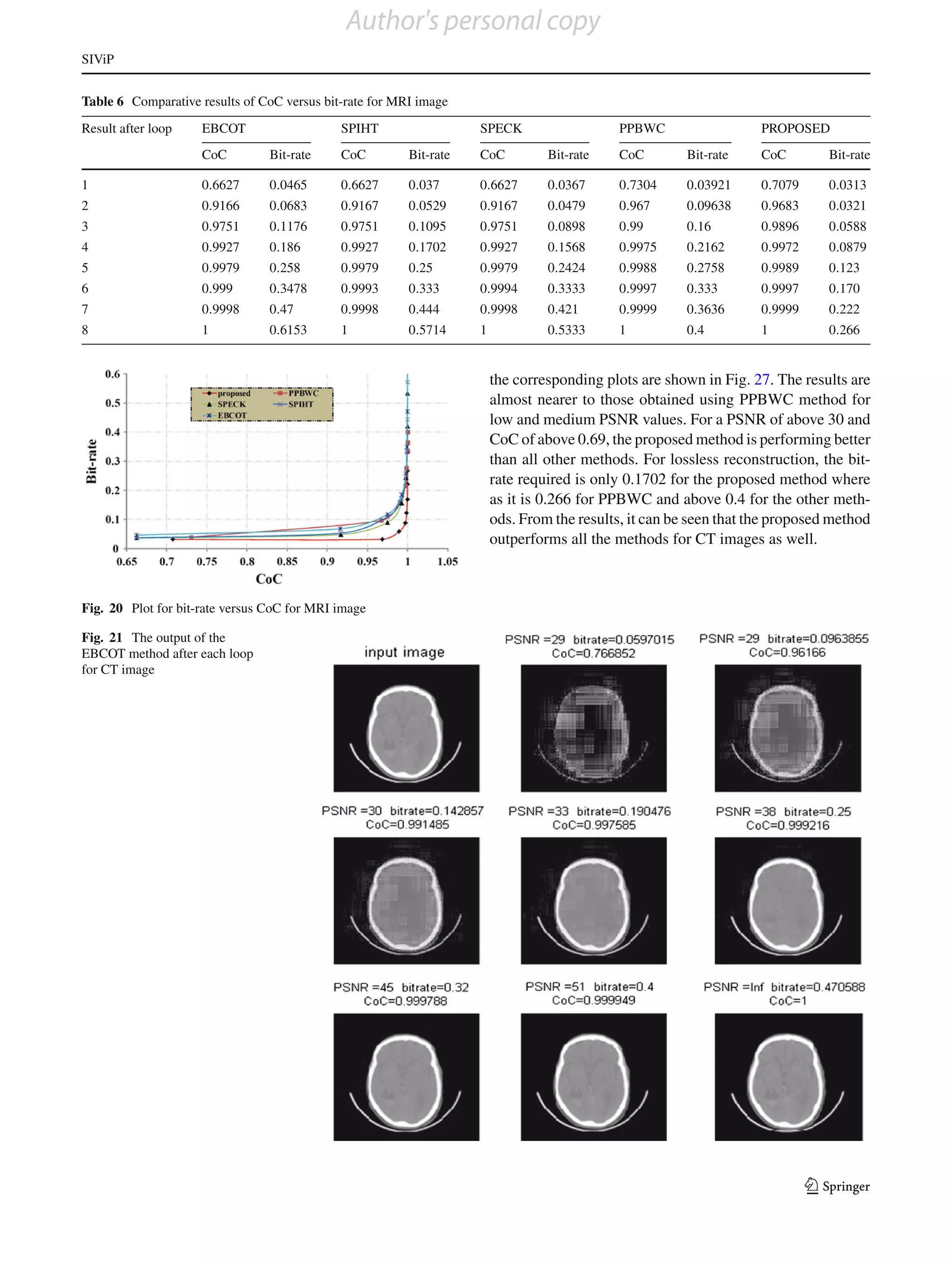
Table 4 Comparative results of CoC versus bit-rate for ultrasound image
CoC Bit-rate CoC Bit-rate CoC Bit-rate CoC Bit-rate CoC Bit-rate

1 0.3496 0.0465 0.3496 0.3137 0.349 0.0313 0.5797 0.03636 0.5723 0.3137
2 0.7968 0.0720 0.7968 0.0571 0.7968 0.057 0.8862 0.1194 0.9711 0.0792
3 0.9366 0.125 0.9366 0.1212 0.9366 0.1066 0.9723 0.2 0.9931 0.1212
4 0.9820 0.21 0.9825 0.2 0.9825 0.2 0.9944 0.2758 0.9985 0.1632
5 0.9956 0.32 0.99 0.3076 0.9956 0.32 0.998 0.32 0.999 0.2051
6 0.998 0.42 0.9989 0.4210 0.9989 0.4 0.9998 0.3636 0.9999 0.25
7 0.999 0.53 0.999 0.533 0.999 0.5 0.9999 0.3809 1 0.2962
8 1 0.666 1 0.6153 1 0.6153 1 0.3892

123

SIViP

EBCOT method after each loop
for MRI image

SPIHT method after each loop
for MRI image

123

SIViP

SPECK method after each loop
for MRI image

PPBWC method after each loop
for MRI image

123

SIViP

proposed method after each loop
for MRI image

Table 5 Comparative results of PSNR versus bit-rate for MRI image

1 28 0.0465 28 0.037 28 0.0367 29 0.03921 28 0.0313
2 29 0.0683 29 0.0529 29 0.0479 33 0.09638 29 0.0321
3 30 0.1176 30 0.1095 30 0.0898 34 0.16 30 0.0588
4 31 0.186 31 0.1702 31 0.1568 37 0.2162 32 0.0879
5 35 0.258 35 0.25 35 0.2424 40 0.2758 37 0.123
6 42 0.3478 42 0.333 42 0.3333 50 0.333 44 0.170
7 48 0.47 48 0.444 48 0.421 59 0.3636 52 0.222
8 Inf 0.6153 Inf 0.5714 Inf 0.5333 Inf 0.4 Inf 0.266

than the existing methods. For lossless reconstruction, the
bit-rate is only 0.266 for the proposed method where as it
is 0.4 for PPBWC, above 0.5 for other methods. From the
results, it is clear that the proposed method outperforms
all the methods for medium and high bit-rates for MRI
images.
For CT images, all type of gray values exists. The outputs
after each loop for each method are shown in Figs. 21, 22, 23,
24 and 25. In each ﬁgure, the ﬁrst image shows the input and
second image onward shows the output after each loop. The
comparative results of the bit-rate versus PSNR are shown
in Table 7, and the corresponding plots are shown in Fig. 26.
Fig. 19 Plot for PSNR versus bit-rate for MRI image
The results for bit-rate versus CoC are shown in Table 8, and

123

SIViP

Table 6 Comparative results of CoC versus bit-rate for MRI image

1 0.6627 0.0465 0.6627 0.037 0.6627 0.0367 0.7304 0.03921 0.7079 0.0313
2 0.9166 0.0683 0.9167 0.0529 0.9167 0.0479 0.967 0.09638 0.9683 0.0321
3 0.9751 0.1176 0.9751 0.1095 0.9751 0.0898 0.99 0.16 0.9896 0.0588
4 0.9927 0.186 0.9927 0.1702 0.9927 0.1568 0.9975 0.2162 0.9972 0.0879
5 0.9979 0.258 0.9979 0.25 0.9979 0.2424 0.9988 0.2758 0.9989 0.123
6 0.999 0.3478 0.9993 0.333 0.9994 0.3333 0.9997 0.333 0.9997 0.170
7 0.9998 0.47 0.9998 0.444 0.9998 0.421 0.9999 0.3636 0.9999 0.222
8 1 0.6153 1 0.5714 1 0.5333 1 0.4 1 0.266

the corresponding plots are shown in Fig. 27. The results are
almost nearer to those obtained using PPBWC method for
low and medium PSNR values. For a PSNR of above 30 and
CoC of above 0.69, the proposed method is performing better
than all other methods. For lossless reconstruction, the bit-
rate required is only 0.1702 for the proposed method where
as it is 0.266 for PPBWC and above 0.4 for the other meth-
ods. From the results, it can be seen that the proposed method
outperforms all the methods for CT images as well.

Fig. 20 Plot for bit-rate versus CoC for MRI image

for CT image

123

SIViP

SPIHT method after each loop
for CT image

SPECK method after each loop
for CT image

123

SIViP

PPBWC method after each loop
for CT image

for CT image

123

SIViP

Table 7 Comparative results of PSNR versus bit-rate for CT image

1 29 0.0597 29 0.0487 29 0.0418 30 0.05263 29 0.0313
2 29.5 0.0963 29.5 0.086 29.5 0.0808 38 0.09195 29.5 0.0329
3 30 0.1428 30 0.1269 30 0.123 40 0.125 30 0.0473
4 33 0.1904 33 0.16 33 0.16 43 0.1568 33 0.0666
5 38 0.25 38 0.2162 38 0.2162 49 0.1904 40 0.09
6 45 0.32 45 0.2857 45 0.2962 55 0.2222 47 0.1159
7 51 0.4 51 0.3636 51 0.3333 63 0.25 55 0.1428
8 Inf 0.47 Inf 0.4444 Inf 0.4 Inf 0.2666 Inf 0.1702

Fig. 26 Plot for PSNR versus bit-rate for CT image Fig. 27 Plot for CoC versus bit-rate for CT image

6 Conclusions proposed method is well established through the results
obtained on ultrasound image of size 640 × 480, MRI and
In this paper, quadtree-based image coding method is CT images of size 512 × 512. From the experimental results,
proposed suitable for medical image coding. It utilizes it is clear that the proposed method outperforms for all the
the energy concentration property of binary wavelet trans- bit-rates on ultrasound and CT images and for bit-rates of
forms in high-frequency subbands. The effectiveness of the above 0.07 on MRI images.

Table 8 Comparative results of CoC versus bit-rate for CT image

1 0.7668 0.0597 0.7668 0.0487 0.7668 0.0418 0.676 0.05263 0.6908 0.0313
2 0.9616 0.0963 0.9616 0.086 0.9616 0.0808 0.9919 0.09195 0.9676 0.0329
3 0.9914 0.1428 0.9914 0.1269 0.9914 0.123 0.998 0.125 0.9953 0.0473
4 0.9975 0.1904 0.9975 0.16 0.9975 0.16 0.9994 0.1568 0.9991 0.0666
5 0.9992 0.25 0.9992 0.2162 0.9992 0.2162 0.9998 0.1904 0.9998 0.09
6 0.9997 0.32 0.9997 0.2857 0.9997 0.2962 0.9999 0.2222 0.9999 0.1159
7 0.9999 0.4 0.9999 0.3636 0.9999 0.3333 0.9999 0.25 0.9999 0.1428
8 1 0.47 1 0.4444 1 0.4 1 0.2666 1 0.1702

123

SIViP

References 15. Pearlman, W.A., Islam, A., Nagaraj, N., Said, A.: Efficient
low-complexity image coding with a set-partitioning embed-
1. Chang, C.C., Shine, F.C., Chen, T.S.: A new scheme of progressive ded block coder. Proc. IEEE Trans. Circuits Syst. Video Tech-
image transmission based on bit-plane method. In: Proceedings of nol. 14(11), 1219–1235 (2004)
Fifth Asian Pacific Conference on Communications and Fourth 16. Taubman, D.: High performance scalable image compression with
Optoelectronics and Communications Conference, Beijing, China, EBCOT. Proc. IEEE Trans. Image Process. 9(7), 1159–1170 (2000)
pp. 892–895 (1999) 17. Pan, H., Siu, W.C., Law, N.F.: Lossless image compression employ-
2. Jiang, J.H., Chang, C.C., Chen, T.S.: Selective progressive image ing binary wavelet transforms. Proc. IET Image Process. 1(4), 353–
transmission using diagonal sampling technique. In: Proceedings 362 (2007)
of International Symposium on Digital Media Information Base, 18. Swanson, M.D., Tewfik, A.H.: A binary wavelet decomposition
Nara, Japan, pp. 56–67 (1997) of binary images. Proc. IEEE Trans. Image Process. 5, 1637–
3. Chang, C.C., Ja, J., Chen, T.S.: A fast reconstruction method for 1650 (1996)
transmitting images progressively. Proc. IEEE. Trans. Consumer 19. Kamstra, L.: The design of linear binary wavelet transforms and
Electron. 44(4), 1225–1233 (1998) their application to binary image compression. In: Proceedings
4. Chung, K.L., Tseng, S.Y.: New progressive image transmission of IEEE International Conference Image Processing, ICIP’03, pp.
based on quadtree and shading approach with resolution control. 241–244 (2003)
Proc. J. Pattern Recognit. 22, 1545–1555 20. Kamstra, L.: Nonlinear binary wavelet transforms and their appli-
5. Hung, K.L., Chang, C.C.: New irregular sampling coding method cation to binary image compression. In: Proceedings of 2003 IEEE
for transmitting images progressively. Proc. IEEE Vis. Image Sig- International Conference Image Processing, pp. 593–596 (2002)
nal Process. 105(1), 44–50 (2003) 21. Gerek, Ö.N., Çetin, A.E., Tewfik, A.H.: Subband coding of binary
6. Yu-Chen, H., Ji-Han, J.: Low complexity progressive image trans- textual images for document retrieval. In: Proceedings of IEEE
mission scheme based on quadtree tree segmentation. Proc. J. Real International Conference Image Processing, ICIP ’96, pp. 899–902
Time Imaging 11, 59–70 (2005) (1996)
7. Wang, L., Goldberg, M.: Progressive image transmission using vec- 22. Pan, H., Jin, L.Z., Yuan, X.H., Xia, X.Y., Xia, L.Z.: Context
tor quantization on images in pyramid form. Proc. IEEE Trans. based embedded image compression using binary wavelet trans-
Commun. 37(12), 1341–1348 (1989) form. Proc. J. Image Vis. Comput. 28, 991–1002 (2010)
8. Goldberg, M., Wang, L.: Comparative performance of pyramid data 23. Law, N.F., Siu, W.C.: A filter design strategy for binary field wave-
structures for progressive image transmission. Proc. IEEE Trans. let transform using the perpendicular constraint. Proc. J. Signal
Commun. 39(4), 540–548 (1991) Process. 87(11), 2850–2858 (2007)
9. Aiazzi, B., Alparone, L., Baronti, S.: A reduced Laplacian pyramid 24. Sweldens, W.: The lifting scheme: a construction of second gener-
for lossless and progressive image transmission. Proc. IEEE Trans. ation wavelets. Proc. SIAM J. Math. Anal. 29(2), 511–546 (1997)
Commun. 44(1), 18–22 (1996) 25. Adams, M.D., Kossentini, F.: Reversible integer-to-integer wave-
10. Qiu, G.: A progressively predictive image pyramid for efficient let transform for image compression: performance evaluation and
lossless coding. Proc. IEEE Trans. Image Process. 8(1), 109– analysis. Proc. IEEE Trans. Image Process. 8(6), 1010–1024 (2000)
115 (1999) 26. Antonini, M., Barlaud, M., Mathieu, P., Daubechies, I.: Image
11. Huang, Y., Driezen, H.M., Galatsanos, N.P.: Prioritized DCT for coding using wavelet transforms. Proc. IEEE Trans. Image Pro-
compression and progressive transmission of images. Proc. IEEE cess. 1, 205–220 (1992)
Trans. Image Process. 1(4), 477–487 (1992) 27. Kanumuri, T., Dewal, M.L., Anand, R.S.: Lossy to lossless medical
12. Shapiro, J.M.: Embedded image coding using zerotrees of wave- image coding using joint bit scanning method. Proc. Comput. Eng.
let coefficients. Proc. IEEE Trans. Image Process. 41(12), 3445– Intell. Syst. 2(4), 101–109 (2011)
3462 (1993) 28. Murala, S, Maheshwari, R.P., Balasubramanian, R.: Directional
13. Zandi, A., Allen, J.D., Schwartz, E.L., Boliek, M.: CREW: com- binary wavelet patterns for biomedical image indexing and
pression with reversible embedded wavelets. In: Proceedings of retrieval. Proc. J. Med. Syst. doi:10.1007/s10916-011-9764-4
IEEE Data Computer Conference, pp. 212–221 (1995)
14. Said, A., Pearlman, W.A.: A new fast and efficient image codec
based on set partitioning in hierarchical trees. Proc. IEEE Trans.
Circuits Syst. Video Technol. 6(3), 243–250 (1996)

123

Springer base paper

More Related Content

What's hot

Similar to Springer base paper

Springer base paper