Downloaded 13 times
Uploaded byDmitriy Selivanov
Recsys matrix-factorizations
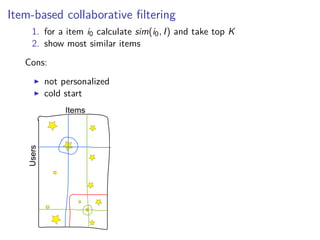
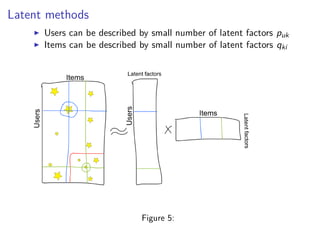
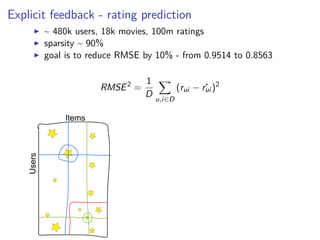
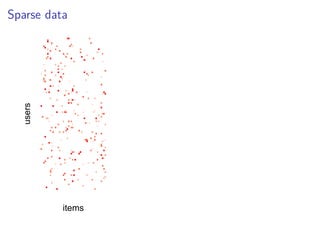
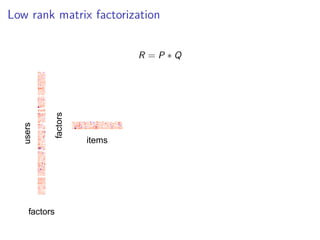
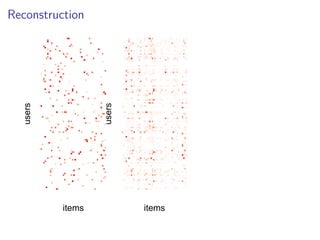
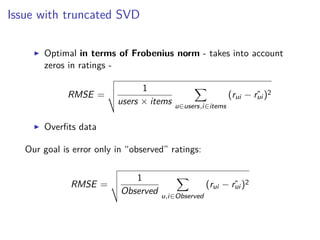
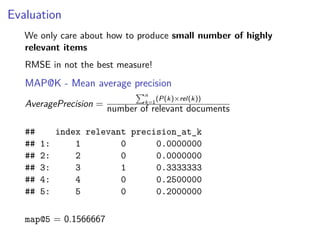
This document discusses matrix factorization techniques for recommender systems. It begins by describing common approaches like content-based, collaborative filtering, and hybrid recommender systems. It then focuses on collaborative filtering, discussing memory and cold start issues with user-based and item-based approaches. The document introduces latent factor models like matrix factorization that address these issues by representing users and items as vectors of factors. It covers optimization techniques like alternating least squares for explicit and implicit feedback datasets. Finally, it discusses evaluation metrics like MAP and NDCG that are more appropriate than RMSE for recommender systems.
Recsys matrix-factorizations
- 1. Matrix Factorizations forRecommender Systems Dmitriy Selivanov 2017-08-26
- 2. Recommender systems areeverywhere Figure 1:
- 3. Recommender systems areeverywhere Figure 2:
- 4. Recommender systems areeverywhere Figure 3:
- 5. Recommender systems areeverywhere Figure 4:
- 6. Goals Personalized offers recommended itemsfor a customer given history of activities (transactions, browsing history, favourites) Similar items substitutions frequently bought together . . . Exploration
- 7.
- 8. Main approaches Content based goodfor cold start not personalized Collaborative filtering vanilla collaborative fitlering matrix factorizations . . . Hybrid and context aware recommender systems best of both worlds
- 9. Collaborative filtering Trivial algorithm: 1.take cutomers who also bought item i0 2. check other items they’ve bought - i1, i2, ... 3. calculate similarity with other items sim(i0, i1), sim(i0, i2), . . . just frequency similarity of the descriptions correlation . . . 4. sort by similarity Cons: recommendations are trivial - usually most popular items not personalized cold start - how to recommend new items? need to keep and work on whole matrix
- 10. User-based collaborative filtering 1.for a user u0 calculate sim(u0, U) and take top K 2. aggregate their opinions about items weighted sum of their ratings Cons: cold start nothing to recommend to new/untypical users need to keep and work on whole matrix
- 11. Item-based collaborative filtering 1.for a item i0 calculate sim(i0, I) and take top K 2. show most similar items Cons: not personalized cold start
- 12. Latent methods Users canbe described by small number of latent factors puk Items can be described by small number of latent factors qki Figure 5:
- 13.
- 14. Explicit feedback -rating prediction ~ 480k users, 18k movies, 100m ratings sparsity ~ 90% goal is to reduce RMSE by 10% - from 0.9514 to 0.8563 RMSE2 = 1 D u,i∈D (rui − ˆrui )2
- 15.
- 16. Low rank matrixfactorization R = P ∗ Q factors users items factors
- 17.
- 18. SVD For any matrixX: X = USV T X ∈ Rm∗n U, V - columns are orthonormal bases (dot product of any 2 columns is zero, unit norm) S - matrix with singular values on diagonal
- 19. Truncated SVD Take klargest singular values: X ≈ UkSkV T k Truncated SVD is the best rank k approximation of the matrix X in terms of Frobenius norm: ||X − UkSkV T k ||F P = Uk √ Sk Q = √ SkV T k
- 20. Issue with truncatedSVD Optimal in terms of Frobenius norm - takes into account zeros in ratings - RMSE = 1 users × items u∈users,i∈items (rui − ˆrui )2 Overfits data Our goal is error only in “observed” ratings: RMSE = 1 Observed u,i∈Observed (rui − ˆrui )2
- 21. SVD-like matrix factorization J= u,i∈Observed (rui − pu × qi )2 + λ(||Q|| + ||P||) Non-convex - hard to optimize, but SGD and ALS works good in practice Alternating Least Squares min i∈Observed (ri − qi × P)2 + λ u j=1 p2 j min u∈Observed (ru − pu × Q)2 + λ i j=1 q2 j Ridge regression: P = (QT Q + λI)−1QT y, Q = (PT P + λI)−1PT y
- 22. Types of feedback Explicit Ratings,likes/dislikes, purchases cleaner data smaller hard to collect Implicit Browsing, clicks, purchases, . . . dirty data larger datasets generally gives better results
- 23. Implicit feedback missed entriesin matrix are mix of negative preferences and positive preferences consider them as negative with low confidence observed entries are positive preferences should have high confidence Model - “Collaborative Filtering for Implicit Feedback Datasets” Preferences Pij = 1 if Rij > 0 0 otherwise Confidence Cui = 1 + f (Rui ) Objective J u=user i=item Cui (Pui − XuYi ) + λ(||X||F + ||Y ||F )
- 24. Alternating Least Squaresfor implicit feedback For fixed Y : dL/dxu = −2 i=item cui (pui − xT u yi )yi + 2λxu = −2 i=item cui (pui − yT i xu)yi + 2λxu = −2Y T Cu p(u) + 2Y T Cu Yxu + 2λxu Setting dL/dxu = 0 for optimal solution gives us (Y T CuY + λI)xu = Y T Cup(u) xu can be obtained by solving system of linear equations: xu = solve(Y T Cu Y + λI, Y T Cu p(u))
- 25. Alternating Least Squaresfor implicit feedback Similarly for fixed X: dL/dyi = −2XT Ci p(i) + 2XT Ci Yyi + 2λyi yi = solve(XT Ci X + λI, XT Ci p(i)) Another optimization: XT Ci X = XT X + XT (Ci − I)X Y T CuY = Y T Y + Y T (Cu − I)Y XT X and Y T Y can be precomputed
- 26. Evaluation We only careabout how to produce small number of highly relevant items RMSE in not the best measure! MAP@K - Mean average precision AveragePrecision = n k=1 (P(k)×rel(k)) number of relevant documents ## index relevant precision_at_k ## 1: 1 0 0.0000000 ## 2: 2 0 0.0000000 ## 3: 3 1 0.3333333 ## 4: 4 0 0.2500000 ## 5: 5 0 0.2000000 map@5 = 0.1566667
- 27. Evaluation NDCG@K - NormalizedDiscounted Cumulative Gain Intuition is the same as for MAP@K, but also takes into account value of relevance. DCGp = p i=1 2reli − 1 log2(i + 1) nDCGp = DCGp IDCGp IDCGp = |REL| i=1 2reli − 1 log2(i + 1)
- 28.