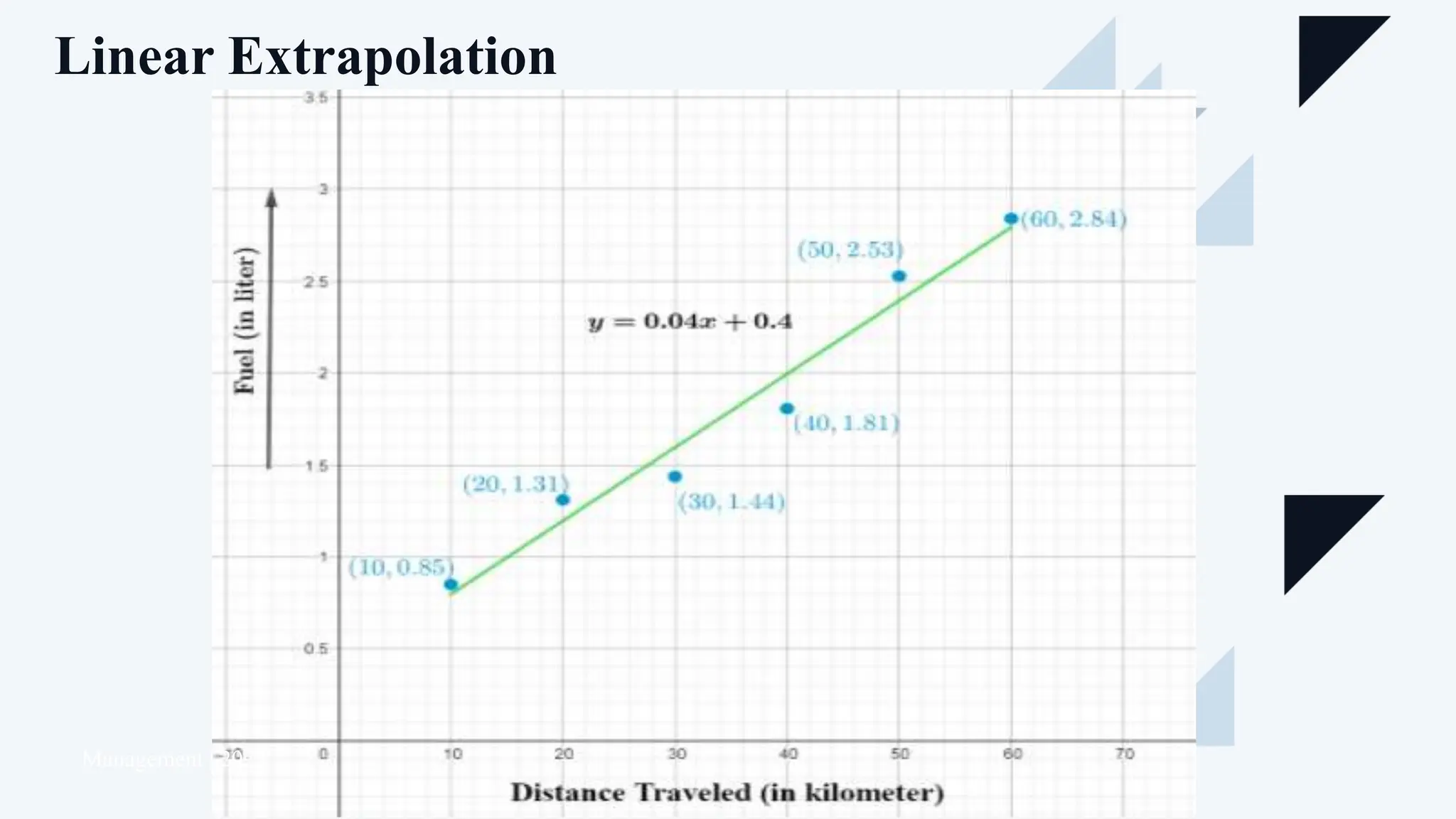
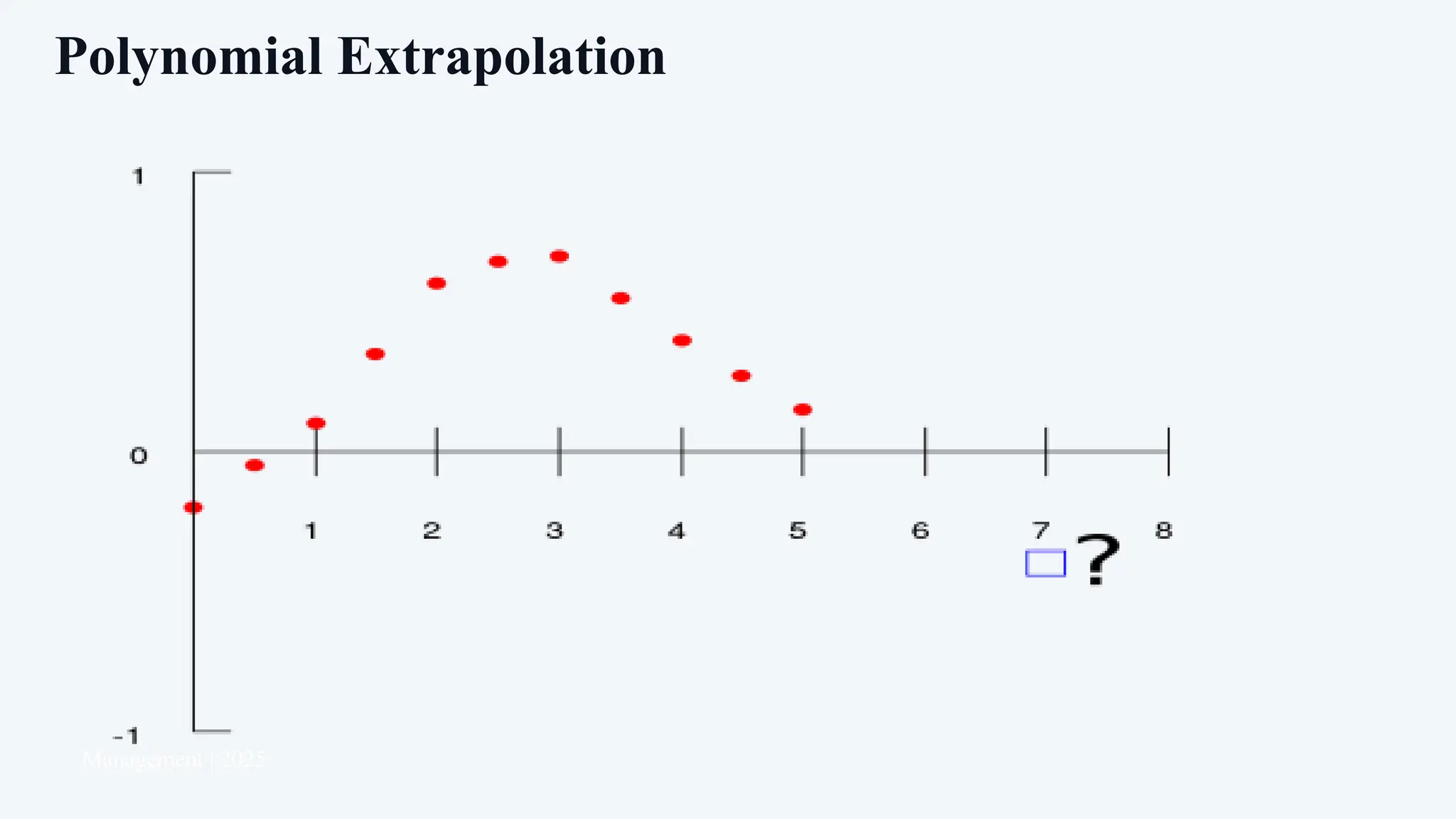
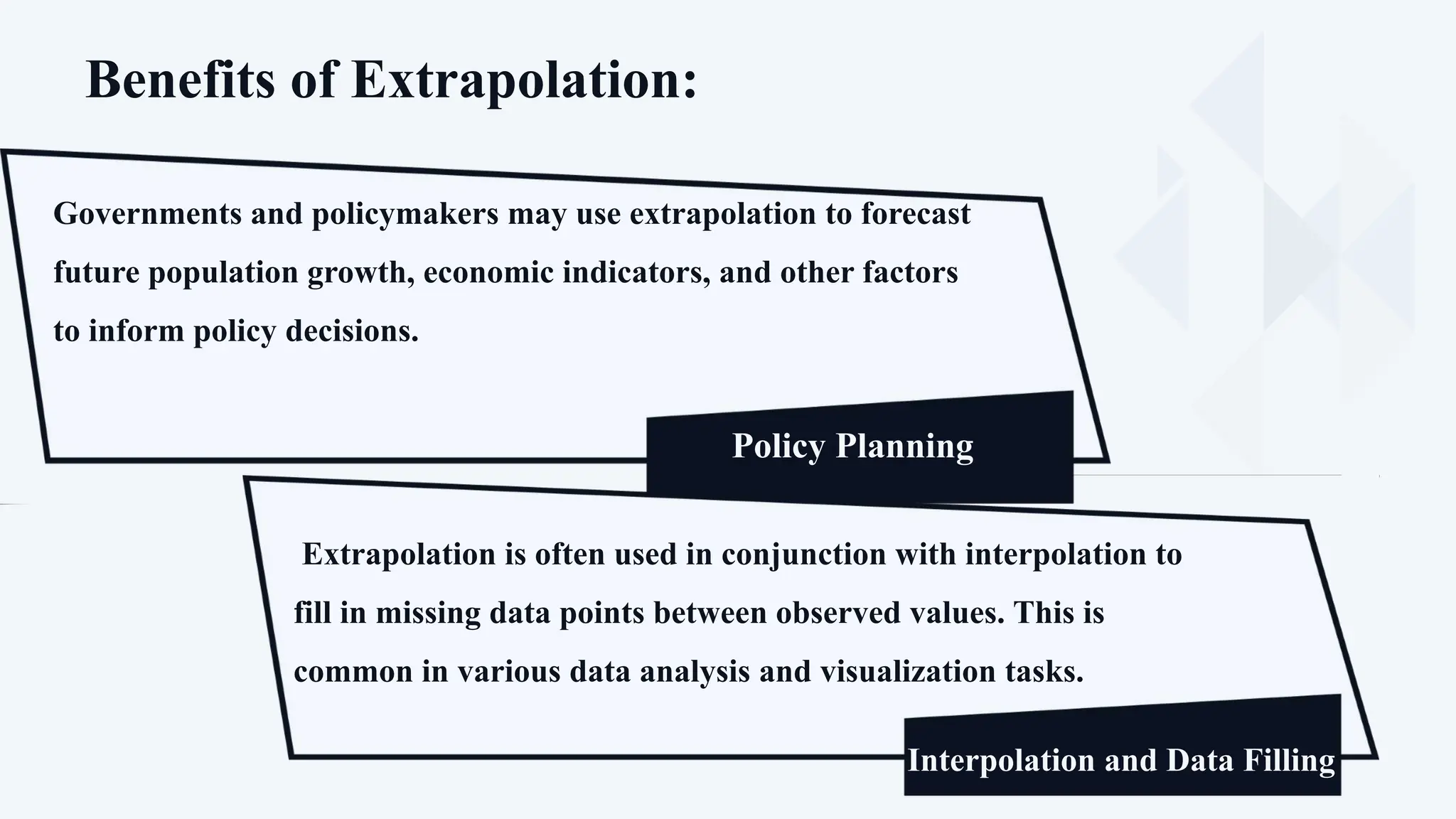
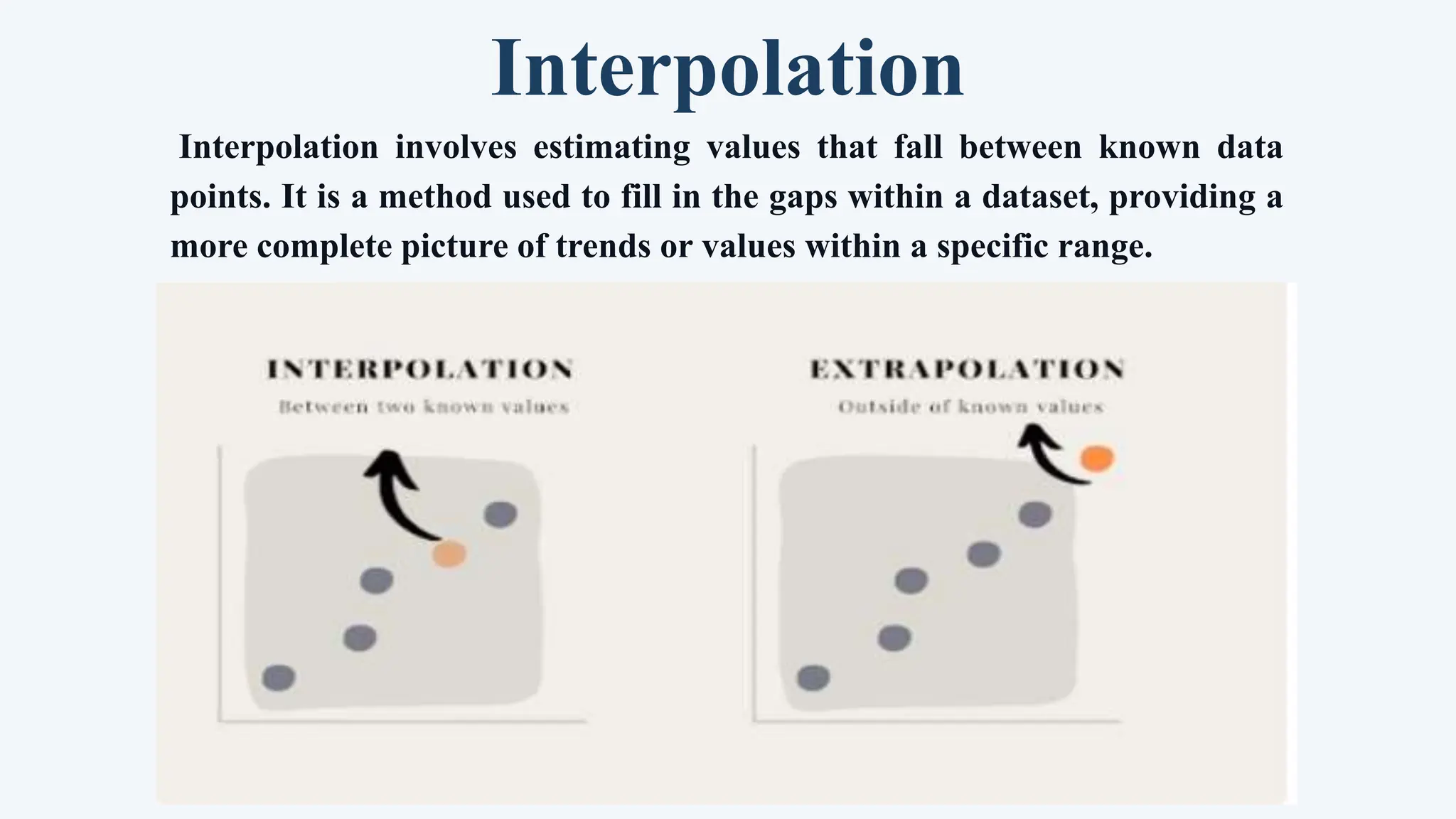
The document discusses extrapolation and interpolation as statistical techniques used to predict and estimate data points beyond or between known values. Extrapolation involves extending trends observed in existing data to make predictions about future values, while interpolation estimates values within the range of known data points. Both methods are essential in various fields such as finance, science, and data analysis, but each comes with its own set of limitations and assumptions that should be considered.