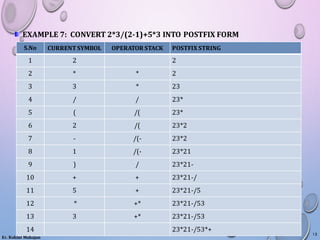
The document explains the conversion of infix expressions to postfix notation, emphasizing the advantages of postfix over infix in terms of ease of evaluation without needing operator priorities or parentheses. It outlines a stack-based algorithm for this conversion, detailing rules for processing operators and operands. Several examples illustrate the step-by-step conversion process, along with C++ code implementations for stack operations.

1. STACKS IN DATA
STRUCTURES:
CONVERSION OF
INFIX
EXPRESSION INTO
POSTFIX
FACULTY: Er. Rohini Mahajan
DEPARTMENT OF CSE
CEC(FOE),JHANJERI

2. WHY TO USE PREFIX AND POSTFIX NOTATIONS WHEN
WE HAVE SIMPLE INFIX NOTATION?
• INFIX notations are not as simple as they seem specially while
evaluating them. To evaluate an infix expression we need to consider
operators’ priority and associative property
e.g. Expression 3+5*4
evaluate to 32 i.e. (3+5)*4 OR to 23 i.e. 3+(5*4).
• To solve this problem precedence or priority of the operators were
defined.
• Operator precedence governs evaluation order. An operator with higher
precedence is applied before an operator with lower precedence
Er. Rohini Mahajan
2

3. INFIX EXPRESSION IS HARD TO PARSE
Need operator priorities, tie breaker,and delimiters.
This makes computer evaluation more difficult than is necessary.
Postfix and prefix expression forms do not rely on operator priorities, a tie
breaker,or delimiters.
Both prefix and postfix notations have an advantage over infix that while
evaluating an expression in prefix or postfix form, we need not consider the
priority and associativeproperty (order of brackets).
e.g. x/y*z becomes */xyz in prefix and xy/z* in postfix.
Both prefix and postfix notations make expression evaluation a lot easier.
So it is easier to evaluate expressions that are in these forms.
Er. Rohini Mahajan
3

4. ADVANTAGES OF POSTFIX:
You don’t need rules of precedence
You don’t need rules for rightand left associativity
You don’t need parentheses to override the above rules
ADVANTAGES OF INFIX:
You grew up with it
It’s easierto see visually what is done first
Er. Rohini Mahajan
4

5. INFIX TO POSTFIX USING STACK
ALGORITHM :
Given an expressionin the infixform.
Create and initializea stack to hold operators.
Print operands as they arrive.
If the stack is empty or contains a left parenthesis on top, push the
incomingoperator onto the stack.
If the incomingsymbol is a left parenthesis, push it on the stack.
If the incoming symbol is a right parenthesis, pop the stack and print the
operators until you see a left parenthesis. Discardthepair of parentheses.
Er. Rohini Mahajan
5

6. INFIX TO POSTFIX USING STACK(CONTD…)
If the incoming symbol has higher precedence than the top of the stack,
push it on the stack.
If the incoming symbol has equal precedence with the top of the stack,
use association. If the association is left to right, pop and print the top of
the stack and then push the incoming operator. If the association is right
to left, push the incoming operator.
If the incoming symbol has lower precedence than the symbol on the top
of the stack, pop the stack and print the top operator. Then test the
incomingoperator againstthe new top of stack.
At the end of the expression, pop and print all operators on the stack. (No
parentheses should remain.)
Er. Rohini Mahajan 6

7. INFIX TO POSTFIX USING STACK
EXAMPLE1: A * B + C becomes A B * C +
We will show this in a table with three columns.
The first will show the symbol currently being read.
The second will show what is on the stack and the third will show the
current contents of the postfix string.
The stack will be written from left to right with the 'bottom' of the stack to
the left.
Er. Rohini Mahajan 7

8. INFIX TO POSTFIX USING STACK
EXAMPLE1: A * B + C becomes A B * C +
S.No CURRENT
SYMBOL
OPERATOR
STACK
POSTFIX STRING
1 A A
2 * * A
3 B * A B
4 + + A B * {pop and print the '*' before pushing
the '+'}
5 C + A B * C
6 A B * C +
Er. Rohini Mahajan
8

9. CONTD…
The rule used in lines 1, 3 and 5 is to print an operand when it is read.
The rule for line 2 is to push an operator onto the stack if it is empty.
The rule for line 4 is if the operator on the top of the stack has higher
precedence than the one being read, pop and print the one on top and
then push the new operator on.
The rule for line 6 is that when the end of the expression has been
reached, pop the operators on the stack one at a time and print them.
Er. Rohini Mahajan
9

10. INFIX TO POSTFIX USING STACK
EXAMPLE2: A + B * C becomes A B C * +
S.No CURRENT
SYMBOL
OPERATOR
STACK
POSTFIX STRING
1 A A
2 + + A
3 B + A B
4 * + * A B
5 C + * A B C
6 A B C * +
In line 4, the '*' sign is pushed onto the stack because it has higher precedence than the '+' sign
which is already there. Then when the are both popped off in lines 6 and 7, their order will be
reversed.
Er. Rohini Mahajan 10

11. INFIX TO POSTFIX USING STACK
EXAMPLE3: A * (B + C) becomes A B C + *
S.No CURRENT
SYMBOL
OPERATOR
STACK
POSTFIX STRING
1 A A
2 * * A
3 ( * ( A
4 B * ( A B
5 + * ( + A B
6 C * ( + A B C
7 ) * A B C +
8 A B C + *
Er. Rohini Mahajan 11

12. INFIX TO POSTFIX USING STACK
EXAMPLE4: A - B + C becomes A B - C +
S.No CURRENT
SYMBOL
OPERATOR
STACK
POSTFIX STRING
1 A A
2 - - A
3 B - A B
4 + + A B -
5 C + A B - C
6 A B - C +
In line 4, the '-' will be popped and printed before the '+' is pushed onto the stack. Both
operators have the same precedence level, so left to right association tells us to do the first
one found before the second.
Er. Rohini Mahajan 12

13. INFIX TO POSTFIX USING STACK
EXAMPLE5: A * B ^ C + D becomes A B C ^ * D +
S.No CURRENT
SYMBOL
OPERATOR
STACK
POSTFIX STRING
1 A A
2 * * A
3 B * A B
4 ^ * ^ A B
5 C * ^ A B C
6 + + A B C ^ *
7 D + A B C ^ * D
8 A B C ^ * D +
Er. Rohini Mahajan 13

14. EXAMPLE6: A * B ^ C + D becomes A B C ^ * D +
S.No CURRENTSYMBOL OPERATOR STACK POSTFIX STRING
1 A A
2 * * A
3 ( * ( A
4 B * ( A B
5 + * ( + A B
6 C * ( + A B C
7 * * ( + * A B C
8 D * ( + * A B C D
9 ) * A B C D * +
10 + + A B C D * + *
11 E + A B C D * + * E
12 A B C D * + * E +
Er. Rohini Mahajan 14

15. EXAMPLE 7: CONVERT 2*3/(2-1)+5*3 INTO POSTFIX FORM
S.No CURRENT SYMBOL OPERATOR STACK POSTFIX STRING
1 2 2
2 * * 2
3 3 * 23
4 / / 23*
5 ( /( 23*
6 2 /( 23*2
7 - /(- 23*2
8 1 /(- 23*21
9 ) / 23*21-
10 + + 23*21-/
11 5 + 23*21-/5
12 * +* 23*21-/53
13 3 +* 23*21-/53
14 23*21-/53*+
Er. Rohini Mahajan
15

16. EXAMPLE 8: CONVERT A+(B*C-(D/E↑F)*G)*H INTO POSTFIX FORM
Er. Rohini Mahajan
16

17. IMPLEMENTATION OF STACK IN C++
#include<iostream>
#include<stack>
usingnamespace std;
int main()
{
stack<int>stck;
int product= 1;
stck.push(1);
stck.push(2);
stck.push(3);
stck.push(4);
stck.push(5);
stck.push(6);
while (!stck.empty()){
product= product* stck.top();
cout<<"n P="<<product;
cout<<"n SIZE OF STACK IS: "<<stck.size();
stck.pop();
}
return 0;
}
OUTPUT:
P=6
SIZE OF STACK IS: 6
P=30
SIZE OF STACK IS: 5
P=120
SIZE OF STACK IS: 4
P=360
SIZE OF STACK IS: 3
P=720
SIZE OF STACK IS: 2
P=720
SIZE OF STACK IS: 1
Er. Rohini Mahajan
17

18. WRITE A PROGRAM TO INSERT FIVE ELEMENTS IN THE STACK AND PRINT THE
TOP ELEMENT USING TOP() AND PRINT THE SIZE OF THE STACK AND CHECK IF
THE STACK IS EMPTY OR NOT.
int main()
{
stack<int> stack1; //empty stack of integer type
stack1.push(100);
stack1.push(200);
stack1.push(300);
stack1.push(400);
stack1.push(500);
cout << "THE TOPMOSTELEMENTOF THE STACK IS:"
<<stack1.top()<< endl;
cout << "THE SIZE OF THE STACK IS=" << stack1.size()
<< endl;
if (stack1.empty())
{
cout<< "STACK IS EMPTY"<< endl;
}
else
{
cout<< "STACK IS NOT EMPTY"<< endl; }}
OUTPUT:
THE TOPMOSTELEMENTOFTHE STACK IS:500
THE SIZE OF THE STACK IS=5
STACK IS NOT EMPTY
Er. Rohini Mahajan
18

19. WRITE A PROGRAM TO INSERT 5 ELEMENTS IN A STACK AND DELETE 2
ELEMENTS THEN PRINT THE STACK.
int main()
{
stack<int> stack1; //empty stack of integer type
stack1.push(100);
stack1.push(200);
stack1.push(300);
stack1.push(400);
stack1.push(500);
stack1.pop();
stack1.pop();
while (!stack1.empty())
{
cout << "Element =" << stack1.top() << endl;
stack1.pop();
}
}
OUTPUT:
ELEMENT =300
ELEMENT =200
ELEMENT =100
Er. Rohini Mahajan
19

20. STACK IMPLEMENTAION USING ARRAY
#include <iostream>
using namespace std;
int stack[100], n = 100, top = -1;
void push(int val) {
if(top >= n-1)
cout<<"stack overflow"<<endl;
else { top++;
stack[top] = val;
}
}
Er. Rohini Mahajan 20

21. STACK IMPLEMENTAION USING ARRAY
void pop() {
if(top <= -1)
cout<<"stack underflow"<<endl;
else {
cout<<"the popped element is "<< stack[top] <<endl;
top--;
}
}
Er. Rohini Mahajan 21

22. STACK IMPLEMENTAION USING ARRAY
void display() {
if(top>= 0) {
cout<<"stack elements are:";
for(int i = top; i>= 0; i--)
cout<<stack[i]<<" ";
cout<<endl;
} else
cout<<"stack is empty";
}
Er. Rohini Mahajan 22

23. int main() {
int ch, val;
cout<<"1)pushin stack"<<endl;
cout<<"2)pop from stack"<<endl;
cout<<"3)display stack"<<endl;
cout<<"4)exit"<<endl;
do {
cout<<"enter choice: "<<endl;
cin>>ch;
switch(ch) {
case 1: {
cout<<"enter valueto be pushed:"<<endl;
cin>>val;
push(val);
break;
}
case 2: { pop();
break;}
case 3: { display();
break;
}
case 4: {
cout<<"exit"<<endl;
break;
}
default: {
cout<<"invalid choice"<<endl;
}
}
}while(ch! = 4);
return 0;
}
Er. Rohini Mahajan
23

24. OUTPUT
1) Pushin stack
2) Pop from stack
3) Display stack
4) Exit
Enter choice: 1
Enter valueto be pushed: 200
Enter choice: 1
Enter valueto be pushed: 300
Enter choice: 1
Enter valueto be pushed: 400
Enter choice: 1
Enter valueto be pushed: 500
Enter choice: 3
Stack elements are:500 400 300200
Enter choice: 2
The popped elementis500
Enter choice: 3
Stack elements are:400 300 200
Enter choice: 4
Er. Rohini Mahajan 24

25. #include<iostream>
#include<stack>
usingnamespace std;
void postfix(char *exp)
{ stack <char> s;
char output[50],t;
for(inti=0;exp[i]!='0';i++)
{ char ch = exp[i];
switch(ch)
{
case '^':
case '-':
case '+':
case '/':
case '*': s.push(ch); break;
C++ PROGRAM TO CONVERT INFIX TO POSTFIX
case ')': t=s.top();
s.pop();
cout<<t;
break;
}
if (isalpha(ch))
cout<<ch;
}
}
int main( )
{
char exp[ ] = "a+b*(c^d-e)^(f+g*h)-i";
postfix(exp);
return 0;
}
25
Er. Rohini Mahajan

26. OUTPUT
CONVERTED POSTFIX EXPRESSION=abcde-fgh*i
Er. Rohini Mahajan 26