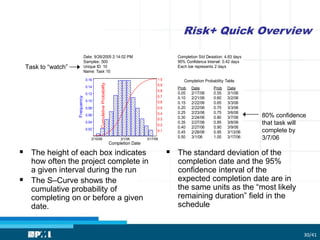
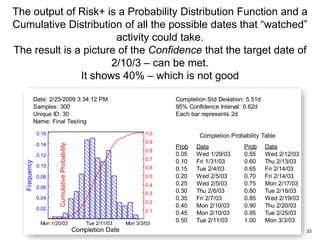
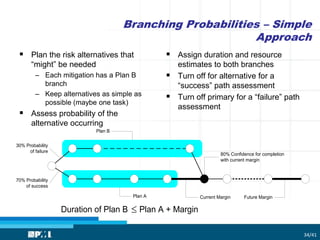
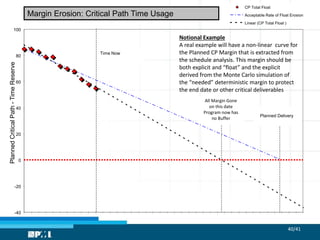
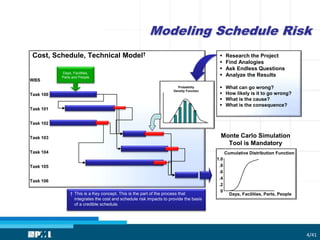
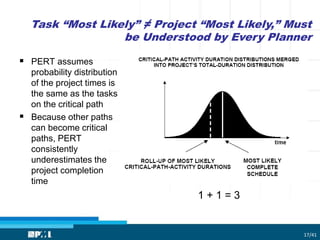
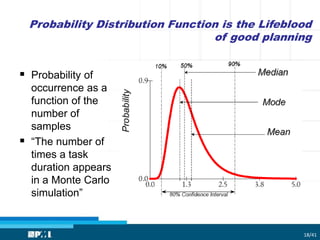
The document focuses on utilizing Monte Carlo simulation to identify schedule margins and manage uncertainties within project scheduling. It contrasts deterministic and probabilistic approaches to scheduling, emphasizing the necessity for proper integration of risk assessments in developing a credible project timeline. Key issues with traditional estimating methods are discussed, highlighting the flaws in single-point estimates and the importance of understanding underlying probability distributions for project duration.

1. Identifying Schedule Margin using Monte Carlo
Simulation
Glen B. Alleman
May 16-18, 2011
PMI EVM Community of Practice
EVM World 2011

2. Our First Order Goal
Develop a resource loaded, risk tolerant,
Integrated Master Schedule, derived from the
Integrated Master Plan that clearly shows the
increasing maturity of the program’s deliverables,
through vertical and horizontal traceability to the
program’s requirements.
2/41

3. Deterministic Versus Probabilistic
3/41
Deterministic
Each activity has a planned value
For the schedule each task has a
predecessor and a successor.
The longest path through the network
is the critical path
The total duration of the project is a
fixed value - it is deterministic
The total cost is the sum of all the
activity costs
Risks are defined and handled as static
entities
Probabilistic
The program elements are not random,
but they are random variables drawn
from a probability distribution.
Three point estimates "can" be used to
describe task duration random
variables
The total duration of the project is a
random number
The total cost is a random number
Risks are stochastic processes that have
probabilistic outcomes for cost,
schedule and technical performance

4. Modeling Schedule Risk
4/41
Cost, Schedule, Technical Model†
WBS
Task 100
Task 101
Task 102
Task 103
Task 104
Task 105
Task 106
† This is a Key concept. This is the part of the process that
integrates the cost and schedule risk impacts to provide the basis
of a credible schedule.
Probability
Density Function
 Research the Project
 Find Analogies
 Ask Endless Questions
 Analyze the Results
 What can go wrong?
 How likely is it to go wrong?
 What is the cause?
 What is the consequence?
Monte Carlo Simulation
Tool is Mandatory
1.0
.8
.6
.4
.2
0
Days, Facilities, Parts, People
Cumulative Distribution Function
Days, Facilities,
Parts and People

5. Breaking News
 DCMA has something to
say about “schedule
margin.”
5/41

6. Implications affecting
compliance
1. Cannot be directly related to a control account because it is not a defined
element of work
2. Cannot be traced to only one CWBS, IMP, and performing organizational
element because it is not a defined element of work, thus
3. Prevents integration of the schedule through the framework of the WBS and
OBS.
4. Does not have associated budget
5. Has no scope
6. Does not consume resources
7. Does not trace to cost/technical artifacts of same
8. Cannot be included on any authorized work scope documentation
9. cannot be traced to only one WBS or OBS element because it is not a defined
element of work
10. Directly impacts the correct calculation of critical path
6/41

7. Schedules Are Networks Of Random Variables not
Collections of Deterministic Statements
 Task completion durations are random variables not just dates:
– These random variables have underlying probability distributions
– These distributions can not be “added” to arrive at a project completion date
– Trying to force the work into a fixed duration does not increase the likelihood of
completion
 The PERT approach to estimating project duration contains several faulty
assumptions:
– The assumed independence is rarely the case
– Uniform distribution of completion times can not be confirmed
– The 3–Point estimates have built in optimistic bias
 Monte Carlo Simulation provides more accurate estimates of project
completion times:
– But only if the network topology is “well formed”
– And if the interactions of the underlying probability distributions are understood
7/41

8. Some “Unpleasant” Questions Can Easily Occur If
We Don’t Pay Attention To The Details
8/41
 What is the degree of risk in our
baseline? How do we measure this
risk?
 What are the branching probabilities
for the critical path in the IMS? How
are they derived?
 How many “near critical” paths will
become critical as the program
proceeds? What drives these?
 Have the “risk drivers” been identified and mitigations put in place
through explicit tasks in the IMS to deal with each identified risk? If
so, how are they shown in the IMS?
 Do we understand the underlying task completion probability
distributions? How are they derived?
 How do these probability distributions change as the program
proceeds? What is the analytical basis for this?

9. 3 Troubles With Deterministic Schedule Estimating
in a Traditional Manner
9/41
1. Single point estimates can be accurate
a) Without stating the distribution
statistics, the number has no frame of
reference
b) The median temperature in Cody
Wyoming is a balmy 78º
c) Don’t be there in February in your shirt
sleeves
2. There is no standard definition for “best” estimate
a) A hoped for best
b) A planned for best
c) The actual best derived from the underlying statistical model
3. Rollup of the “most likelies” is not the same as Most Likely Total
Duration
a) They are probability distributions not integers
b) Probability distribution function (pdf) convolution is needed
The flaw with using averages alone
Average depth is 3 feet

10. No Single Point Estimate Can Be Accurate, Since
It Ignores The Underlying Statistics
10/41
 Schedule durations are always vague
in the beginning
– Existing technical capability often falls
short of project needs
– Firm requirements, especially
software requirements cannot be
described in a simple list
– “Normal” schedule slippage of
varying lengths result from integration
problems and test failures
– Various other anticipated and
unforeseen events resulting from the
natural variation (Deming variation)
 “Point” estimates can not be correct because…
– Task point estimates of activity durations are not correct
– Project point estimate is the sum of these “incorrect” activity estimates
 “Actual” project duration will fall within some range around the point estimate
– The best that can be done is to understand the uncertainty

11. The Traditional Roll Up Approach Starts with the
“Best” estimates for the Most Likely Durations
 Build a network of the project’s activities
 Determine the “best” estimate of the duration for each
activity in the network
 Compare the activities’ “best” estimates to find the
critical path
 Sum all the “best estimate” durations of activities on the
critical path
 Define this sum of tasks to be “best” estimate of the
project’s schedule duration
 This will almost always be optimistically wrong
 Or it is pessimistically wrong
 Either way – it is wrong
11/41

12. The Problem is the Term “Best” Has
No Standard Definition
 For each activity the “best” estimate is …
– The “most likely” duration – the mode of the distribution of
durations? (Mode is the number that appears most often)
– It’s 50th percentile duration – the median of the distribution?
(Median is the number in the middle of all the numbers)
– It’s expected duration – the mean of the distribution? (Mean
is the average of all the numbers)
 These definitions lead to values that are almost always
different from each other
 Rolling up the “best” estimate of completion is almost
never one of these.
12/41

13. Durations Are Probability Samples not
Single Point Values
 We know this because…
– “Best” estimate is not the only possible estimate, so other
estimates must be considered “worse”
– Common use of the phrase “most likely duration” assumes that
other possible durations are “less likely”
– “Mean,” “median,” and “mode” are statistical terms characteristic
of probability distributions
 This implies activity distributions have probability distributions
– They are random variables drawn from the probability distribution
function (pdf)
 “Actual” project duration is an uncertain quality that can be
modeled as a sum of random variables
– The pdf may be known or unknown
13/41

14. Durations are Educated “Guesses,” but Rarely
Have underlying Probability Distributions
 Define the problem
 Identify the prediction variable
 Build the prediction model
– Develop a list of relevant factors
– Consider the effects
– Collect data
– Plot each factor independently
– Develop a prediction model using linear regression
– Understand the model
– Check the model
 Make guesses with the model
 Take care with the results
14/41

15. Modeling Duration Probability starts with experts
but must include statistical estimates
 Compile duration estimates from different sources and rank
the estimates:
– Subcontractors or IPTs estimate
– Project manager’s estimate
– “Independent” estimate
– Risk–impacted estimate
 Associate confidence levels with ranges between estimates,
using information available from different situations and at
different stages in the project development cycle
– These can not be looked up in a book
– Are not directly derived from historical data
– Must be subjective, knowledge based consensus of technical
experts in a particular WBS
– Should be a standard part of the risk mitigation plan
15/41

16. Mr. Gauss’s Distribution is found in many text
book examples, too bad is not applicable
16/41
 The Gaussian distribution can be proved (by the Central Limit
Theorem) in the situation that each measurement is the result of a
large amount of small, independent error sources. These errors have
to be of the same magnitude, and as often positive as negative.
 When a physical item is
measured and systematic errors
are eliminated the measured
values will spread around the
average value.
 The average value of a measured
value is the “best value.”

17. Task “Most Likely” ≠ Project “Most Likely,” Must
be Understood by Every Planner
17/41
 PERT assumes
probability distribution
of the project times is
the same as the tasks
on the critical path
 Because other paths
can become critical
paths, PERT
consistently
underestimates the
project completion
time
1 + 1 = 3

18. Probability Distribution Function is the Lifeblood
of good planning
18/41
 Probability of
occurrence as a
function of the
number of
samples
 “The number of
times a task
duration appears
in a Monte Carlo
simulation”

19. Approaches to Decisions with
Uncertainty
19/41
 Decision trees
 Line of balance
 PERT
 Monte Carlo

20. PERT As The Starting Point For
Probabilistic Schedule Management
20/41
 PERT is a method to determine how long a project should take
– Which activities are most critical
– Deterministic PERT and Probabilistic PERT are common
 PERT algorithms
– Activity duration:
– Activity Standard Deviation:
– Activity Variance:
– Total Standard Deviation:
 4 /6et a m b  
 /6et b a  
 
22
/6ev t b a     
   
2 2
1 2e e eT t t   

21. Deterministic PERT Uses The Three
Point Estimates In A Static Manner
21/41
 Durations are defined as three point estimates
– These estimates are very subjective if captured individually by asking…
– “What is the Minimum, Maximum, and Most Likely”
 Critical path is defined from these
estimates is the algebraic addition
of three point estimates
 Project duration is based on the
algebraic addition of the times
along the critical path
 This approach has some serious
problems from the outset
– Durations must be independent
– Most likely is not the same as the
average

22. Probabilistic PERT Uses The Underlying
Probability Distributions For Each Task
22/41
 Any path could be critical depending on the convolution of the underlying task
completion time probability distribution functions
 The independence or
dependency of each task with
others in the network, greatly
influences the outcome of the
total project duration
 Understanding this
dependence is critical to
assessing the credibility of the
plan as well as the total
completion time of that plan

23. Statistics V. Probability – We Need Both To Build
A Risk Tolerant Schedule
23/41
 In building a risk tolerant IMS,
we’re interested in the probability
of a successful outcome:
– “What is the probability of making
a desired completion date?”
 But the underlying statistics of the
tasks influence this probability
 The statistics of the tasks, their
arrangement in a network of tasks
and correlation define how this
probability based estimated
developed.
Statistical thinking will one day be as
necessary for efficient citizenship as the
ability to read and write.
– H.G. Wells

24. The Dreaded 3–Point Estimates
24/41
 Optimistic Estimate
– The shortest duration
– “It can’t be done in less time than this”
 Most Likely Estimate
– The median time (middle most), not
the mean time (the average)
– This builds in a symmetric distribution
of the probability distribution function
 Pessimistic Estimate
– The additional time needed if things go
wrong
– It is not the maximum time it would
take
– It is not a “worst case scenario”
estimate

25. Thinking About Risk Classification
25/41
 These classifications can be used to avoid asking the “3 point”
question for each task
 This information will be maintained in the IMS
 When updates are made the percentage change can be applied
across all tasks
Classification Uncertainty Overrun
A Routine, been done before Low 0% to 2%
B Routine, but possible difficulties Medium to Low 2% to 5%
C Development, with little technical difficulty Medium 5% to 10%
D Development, but some technical difficulty Medium High 10% to 15%
E Significant effort, technical challenge High 15% to 25%
F No experience in this area Very High 25% to 50%

26. Steps in Characterizing Uncertainty in Task
Duration Estimating Data
26/41
 Use an “envelope” method to characterize the minimum, maximum
and “most likely”
 Fit this data to a statistical distribution
 Use conservative assumptions
 Apply greater uncertainty to less mature technologies
 Confirm analysis matches intuition
Remember Sir Francis Bacon’s quote about
beginning with uncertainty and ending with
certainty.
If we start with a what we think is a valid number
we will tend to continue with that valid number.
When in fact we should speak only in terms of
confidence intervals and probabilities of success

27. Some Sobering Observations
 In 1979, Tversky and Kahneman proposed an alternative to utility
theory. Prospect theory asserts that people make predictably irrational
decisions. [45], [52]
 The way that a choice of decisions is presented can sway a person to
choose the less rational decision from a set of options.
 Once a problem is clearly and reasonably presented, rarely does a
person think outside the bounds of the frame.
 Source:
– “The Causes of Risk Taking By Project Managers,” Proceedings of
the Project Management Institute Annual Seminars & Symposium
November 1–10, 2001 • Nashville, Tenn
– Tversky, Amos, and Daniel Kahneman. 1981. The Framing of
Decisions and the Psychology of Choice. Science 211 (January 30):
453–458
27/41

28. A Quick Look at Monte Carlo
Simulation
George Louis Leclerc, Comte de
Buffon, asked what was the
probability that the needle would
fall across one of the lines, marked
here in green. That outcome will
occur only if
sinA l 
28/41

29. Risk+ Quick Overview
29/41
Task to “watch”
(Number3)
Most Likely
(Duration3)
Pessimistic
(Duration2)
Optimistic
(Duration1)
Distribution
(Number1)

30. Risk+ Quick Overview
30/41
 The height of each box indicates
how often the project complete in
a given interval during the run
 The S–Curve shows the
cumulative probability of
completing on or before a given
date.
 The standard deviation of the
completion date and the 95%
confidence interval of the
expected completion date are in
the same units as the “most likely
remaining duration” field in the
schedule
Date: 9/26/2005 2:14:02 PM
Samples: 500
Unique ID: 10
Name: Task 10
Completion Std Deviation: 4.83 days
95% Confidence Interval: 0.42 days
Each bar represents 2 days
Completion Date
Frequency
CumulativeProbability
3/1/062/10/06 3/17/06
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
0.02
0.04
0.06
0.08
0.10
0.12
0.14
0.16 Completion Probability Table
Prob ProbDate Date
0.05 2/17/06
0.10 2/21/06
0.15 2/22/06
0.20 2/22/06
0.25 2/23/06
0.30 2/24/06
0.35 2/27/06
0.40 2/27/06
0.45 2/28/06
0.50 3/1/06
0.55 3/1/06
0.60 3/2/06
0.65 3/3/06
0.70 3/3/06
0.75 3/6/06
0.80 3/7/06
0.85 3/8/06
0.90 3/9/06
0.95 3/13/06
1.00 3/17/06
Task to “watch”
80% confidence
that task will
complete by
3/7/06

31. Schedule Contingency Analysis
31/41
 The schedule contingency needed
to make the plan credible can be
derived from the Risk+ analysis
 The schedule contingency is the
amount of time added (or
subtracted) from the baseline
schedule necessary to achieve the
desired probability of an under run
or over run.
 The schedule contingency can be determined through
– Monte Carlo simulations (Risk+)
– Best judgment from previous experience
– Percentage factors based on historical experience
– Correlation analysis for dependency impacts
Is This Our
Contingency
Plan ?

32. 32
Schedule for a Monte Carlo Risk analysis starts with a
credible schedule and defines the probabilistic behavior
of each activities and how it drives the deliverables
The Risk+ tool sets the upper and lower bounds of the possible durations

33. 33
Date: 2/25/2009 3:34:12 PM
Samples: 300
Unique ID: 30
Name: Final Testing
Completion Std Deviation: 5.51d
95% Confidence Interval: 0.62d
Each bar represents 2d
Completion Date
Frequency
CumulativeProbability
Tue 2/11/03Mon 1/20/03 Mon 3/3/03
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
0.02
0.04
0.06
0.08
0.10
0.12
0.14
0.16 Completion Probability Table
Prob ProbDate Date
0.05 Wed 1/29/03
0.10 Fri 1/31/03
0.15 Tue 2/4/03
0.20 Wed 2/5/03
0.25 Wed 2/5/03
0.30 Thu 2/6/03
0.35 Fri 2/7/03
0.40 Mon 2/10/03
0.45 Mon 2/10/03
0.50 Tue 2/11/03
0.55 Wed 2/12/03
0.60 Thu 2/13/03
0.65 Fri 2/14/03
0.70 Fri 2/14/03
0.75 Mon 2/17/03
0.80 Tue 2/18/03
0.85 Wed 2/19/03
0.90 Thu 2/20/03
0.95 Tue 2/25/03
1.00 Mon 3/3/03
The output of Risk+ is a Probability Distribution Function and a
Cumulative Distribution of all the possible dates that “watched”
activity could take.
The result is a picture of the Confidence that the target date of
2/10/3 – can be met.
It shows 40% – which is not good

34. Branching Probabilities – Simple
Approach
34/41
 Plan the risk alternatives that
“might” be needed
– Each mitigation has a Plan B
branch
– Keep alternatives as simple as
possible (maybe one task)
 Assess probability of the
alternative occurring
 Assign duration and resource
estimates to both branches
 Turn off for alternative for a
“success” path assessment
 Turn off primary for a “failure” path
assessment
30% Probability
of failure
70% Probability
of success
Plan B
Plan A Current Margin Future Margin
80% Confidence for completion
with current margin
Duration of Plan B Plan A + Margin

35. Managing Margin in the Risk Tolerant IMS
requires the reuse of unused durations
35/41
 Programmatic Margin is added
between Development, Production and
Integration & Test phases
 Risk Margin is added to the IMS where
risk alternatives are identified
 Margin that is not used in the IMS for
risk mitigation will be moved to the next
sequence of risk alternatives
– This enables us to buy back schedule
margin for activities further downstream
– This enables us to control the ripple
effect of schedule shifts on Margin
activities
5 Days Margin
5 Days Margin
Plan B
Plan A
Plan B
Plan AFirst Identified Risk Alternative in IMS
Second Identified Risk
Alternative in IMS
3 Days Margin Used
Downstream
Activities shifted to
left 2 days
Duration of Plan B < Plan A + Margin
2 days will be added
to this margin task
to bring schedule
back on track

36. Examples Of Monte
Carlo
A simple overview of Risk+ shows how to produce
an estimate of a project completion date.
Interpreting this information takes thought and
practice and most importantly reading and
rereading the manual and the resources provided
at the end of this presentation
Sewall Wright’s
probabilistic
network notation
(1921)
36/41

37. The Baseline Schedule
 Sample construction project plan
37/41

38. PERT Assessment
Most
Likely
Min Max
PERT Adjusted Duration
PERT Adjusted Date
Original Target Date: 2/8/06
38/41

39. Risk+ Assessment
Most
Likely
Min Max
Date: 10/4/2005 1:58:06 PM
Samples: 23
Unique ID: 143
Name: Construction Schedule Margin
Completion Std Deviation: 1.55 days
95% Confidence Interval: 0.63 days
Each bar represents 1 day
Completion Date
Frequency
CumulativeProbability
2/9/062/3/06 2/14/06
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
0.05
0.10
0.15
0.20
0.25
0.30
0.35 Completion Probability Table
Prob ProbDate Date
0.05 2/6/06
0.10 2/6/06
0.15 2/7/06
0.20 2/7/06
0.25 2/7/06
0.30 2/8/06
0.35 2/8/06
0.40 2/9/06
0.45 2/9/06
0.50 2/9/06
0.55 2/9/06
0.60 2/9/06
0.65 2/9/06
0.70 2/10/06
0.75 2/10/06
0.80 2/10/06
0.85 2/10/06
0.90 2/10/06
0.95 2/10/06
1.00 2/14/06
Target Date
80% confidence
39/41

40. 40/41
-40
-20
0
20
40
60
80
100
PlannedCriticalPath-TimeReserve
CP Total Float
Acceptable Rate of Float Erosion
Linear (CP Total Float )
Time Now
Planned Delivery
Margin Erosion: Critical Path Time Usage
All Margin Gone
on this date
Program now has
no Buffer
Notional Example
A real example will have a non-linear curve for
the Planned CP Margin that is extracted from
the schedule analysis. This margin should be
both explicit and “float” and the explicit
derived from the Monte Carlo simulation of
the “needed” deterministic margin to protect
the end date or other critical deliverables

41. 41/186
What is the
Purpose of
Schedule Risk
Analysis?
What do users want from a project risk
analysis?
How accurate must we be to provide value to
the program?
Can we confirm this accuracy and integrity to
build confidence in the projected completion
date?
: What is the Purpose of Project Risk Analysis?
Risk appears in all aspects of spaceflight

42. Accuracy
 Given a specified final cost or project duration, what
is the probability of achieving this cost or duration?
 Frequentist approach
– Over many different projects, four out of five will cost
less or be completed in less time than the specified cost
or duration
 Bayesian approach
– We would be willing to bet at 4 to 1 odds that the project
will be under the 80% point in cost or duration
 Accuracy is needed to plan reserves
 Accuracy is needed when comparing competing
proposals
42/186: What is the Purpose of Project Risk Analysis?

43. 43/186
Structured Thinking
 All estimates will be in error
 Trying to quantify these errors will result in bounds
too wide to be useful for decision making
 Risk analysis should be used to
– Think about different aspects of the project
– Try to put numbers against probabilities and impacts
– Discuss with colleagues the different ideas and
perceptions
 Thinking things through carefully results in
– Which elements of the programmatic and technical risk
are represented in the IMS
– The process becomes more valuable than the numbers
: What is the Purpose of Project Risk Analysis?