The document reviews various credit scoring models and statistical methods, emphasizing the use of logistic regression (LR), neural networks (ANN), and genetic algorithms (GA) for assessing credit risk. It discusses the importance of data quality and explores emerging models like multidimensional neural networks and Bayesian inference, aiming to maximize predictive accuracy and minimize errors in credit default predictions. Key findings indicate that while predictive capabilities range from 70-80% accuracy, challenges remain in achieving high accuracy, particularly in homogeneous populations.

1. Eero Siljander VALLUM / BI DEPARTMENT
VTL, VTM, IPMAD 2020-10, October.
CREDIT SCORING MODELS – SMALL LITERATURE REVIEW .V3
SHORT SUMMARY:
Currentmodelsandprograms(R,Python):the baseline or standardmethodforcreditscoringby
statistical methodsislogisticregression(LR). Newmethodsincludeneural networks(ANN),genetic
algorithms(GA),non-parametricmethods(discriminantanalysis(LDA),K-nearestneighborscoring
(whichisa non-parametricmethod),roughestimation(RE),decisiontree (DT) algorithmC4.5or
CART.Most oftenatleast2-3 methodsare usedandcompared.The leastisto compare LR models
withdifferentfixed- andrandomparameterandpanel datamodels.Mostoftenusedmethods
currentlyare LR, ANN,GA,DT. Each of these have theirprosandcons.Proportional hazardand
Weibull hazardare usedforSME data by Rabobank.DeloitteusesLRforB2C consumercreditdata.
You can do manyof these withRstudios,Python.
Proof of-Case (Stata):a) Statasoftware offersinaddition neural networks,partial creditscoring
models(EMoptimization) andItem-response &Raschmodels.The advantage withStataisthat you
can calculate derivativesandelasticityof X-variables.b) Thatisa change% inprobabilityof defaultor
otherY-variable withrespecttoone%change incontinuesX(income say) orc) classificationvariable
X (marital status,numberof creditcardsetc.),d) we getresultsintoExcel andPdf-tables,e) we can
applyBaysestimationinadditiontoMLE and mathematical techniques.We getHighValue Addedby
adoptingthisSoftware!See P) belowformore detailsatthe endof thispaper.
Goal: Maximize discriminatorypowerof X-variableswithrespecttoY-variables.Findright
explanatoryX-variables.Targetondefault-risk,bankruptcyrisk,
TARGET FOR ANALYSIS:
1) We wantto maximize discriminatorypowerof X-variableswithrespecttoY-variables,
2) We wantto minimize Type IIerror(1- Type II error = Right classificationof defaulters,inpercent,
%),
3) maximize Log-likelihoodorminimize MSE-errorforstatistical methods.
4) Maximize areaunderROC-curve.
5) Minimize model ERRORRATES,whethermathematical orstatistical.
Thiscan be inmany casesall done at the same time usingbestfittingstatistical ormathematical
modelsandcomparingbasedonthese TARGETS above.
Emergingmodels:Neural networkswithmultidimensional-layers(SVM),Bayesianinference (BI) of
creditworthinessprobabilities (priorandposteriordistributions)andAIC/BIC-informationcriterion
to compare goodness-of-fitof statistical models.Propensityscore matching(commoneconometrics
method) couldbe yetanothermethodtobe tried(notfoundinliterature reviewed).A good
reference forpropensityscore matchingisUusitalo&Korkeamäki 2003 (Employmenteffectsof a
payroll tax cut – Evidence fromaregional tax exemptionexperiment).The ideaistomatch X-
variablessothatdifferentgroupscanbe comparedbasedon similarityasopposedtodiscriminant
that isbaseline increditscoringdecision(creditworthyvsnon-creditworthy). Whatthingsunite
“good” riskfor example.Orderedlogit(OLR) andRandomParameterLogit(RPL) modelsshouldbe
triedoutbecause theyare newin standardmethods.

2. There are twocreditmodelingdomains:1) Origination score usedtopredictwhethertogive aloan
to someone 2) Behavioral modelsusedtopredictcustomerhistoryandbehaviorrelatedvariablesto
predictcollectionorline of creditperformance laterinthe life of loanproduct.
Data: our data is inthe range N=10 000 – 100 000 etc.This isdescribedindetail inHand& Henley
1997 althoughtheirmethodsare obsoleteandratherold.Data usedinthe researchliterature
usuallyconsistsof (somewhatunfortunately)about1 000 – 4 000 observationsof which70-90 % are
“good” riskcreditand 5-30 % “bad” creditrisk.Whennewestandinsome sense “most-fashionable”
geneticalgorithmsare usedtheyworkbestinthe situationwhere“bad”and“good” riskare 50-50
%. Howeverthisisquite rare instandardcreditrating. Data Qualityisabsolutelykeyforgood
Results! Inmostof the academicresearchitis not as goodas hoped.
Missingdata andoutlieranalysisare coveredindetail Hand&Henley1997. Alsoin Deloitte’spaper.
We needtoreplace missingdatabysome methods(ordropdata as lastresort).Outlierdetectionby
explorativeanalysisandboxplotsiskeyinpreliminaryphase of analysis.Inregressionanalysisitis
well knownthatinfluential observationscanchange resultstosome extentinanot-wished
direction.
Y-values:Desai et.al.1997 go through3 modesmostextensively(”good”,”intermediate”and”bad”
riske.g.creditworthiness,fringe.casesanddefaulters.).Inotherresearchusuallyonlycreditworthy
(non-default)“good”riskandnon-creditworthy(default) “bad”riskare examined.HandandHenley
(1997) describe indetail whatcreditscoringandcreditratingcan be usedfor inALL aspects.Models
can be continuesscore-cards(continuesY) ordiscrete outcome Y(creditworthyvs.non-
creditworthy).
X-values:Desai et.al.1997 and Hand & Henley1997 go throughX-valuesorAttributesor
Characteristic.MostresearchpapersreviewedcategorizeanddiscretizecontinuosX-variables.For
example incomeorage are put intogroups.
Missingvalues:Hand & Henley1997 tacle thisand X’sindepth.Missingvaluesare alsoreviewed
extensivelyinthe Deloitte paper.One canreplace themwithvarioustechniquesandboxplot
outliers.See DeloitteandHand& Henley.
Results:basedonthe reviewedliterature workextremelywellthe statisticalmodelspredictabout
70-80 %of DEFAULT RISK correctly.Howeverforhighcreditworthiness(“good”risk) orsome-trouble
of pay“intermediate”riskthe modelsworklesswell (50-60% correct prediction) Thisisagood value
accordingto statisticsprofessorSeppoMustonen(Multivariete methods-book,Univof Helsinki,
1995) whoisa specialistof discriminantanalysisandAImethods. Itishard to go above 90 % correct
prediction evenwithoriginal population data.We are alwaysworking with sampledata.Thisisthe
mostimportantriskwhenconsideringprofit.Thisisusuallyachievedinthe heterogenous(general)
population.Inpractice,variableimportance rankingsinLRmodels canbe usedto testone way
interactioneffects andaddthemto logitmodels,resultinginperformance whichmatchesor
sometimesoutperformsrandomforests
Howeverwhenpopulationishomogenous(forexamplea) only teachersor b) only telephone
company employees) the modelscansometimesgive onlyatbest50 % correct predictionfor “good”
or “intermediate”riskthe correctpredictionisinmostcasesat bestevenwithANN anddifferent
optimizationmethods.The errorrate of predictionvariesinarecentpaperwithAustralianand
Germandata from 10 to 40 %.
Papersreviewed:literature searchbyGoogle onterms“creditscoring”and“statistical methods”.
Thisleadsto papersinthe range of 10 pieceswhere logisticregressionandneural networksand
non-parametricmethodsare discussed.Sorteddescendingbyrelevancebelowexcept forpaperN)
that shouldbe starting pointfor any readingof the creditscoring literature.

3. 5 KEY PRINCIPLESFOUNDIN LITERATURE
1. “A creditscoringmodel isjustone of the factorsused inevaluatingacreditapplication.
Assessmentbya creditexpertremainsthe decisivefactor” – Deloitte,riskscorers,2016.
2. “For CreditCompanyprofititismostimportantto classifyRightthose inRiskof Default” -Ophal
et.al.,2017.
3. “It isimportantto getevena 0,1 % increase inthe fittingof the model,e-g-probabilitiesof
defaultandcreditworthiness”-Almostall academicresearchpapers.
4. “Experimentwithmanystatistical methods(ANN,LDA,GA,k-nearestneigh.) andcompare the
ROC,AUC, correct classificationof customersbyPROBABILITYresultsholdinglogisticregression
LR as baseline”-industrystandard,Deloitte,2016.
5. “Compare expertcreditdecisionwithcreditscoringstatistical decision –same or not, if not
Why?” -Deloitte,2016.
EVALUATION OFPAPERS
In thisdocumentwe reportthe keyFindingsof eachreportor researchpaperas follows.The focus:
1. Data and its keyattributes usedinthe researchpaperinquestion(Possiblya
subjective evaluationof quality).
2. Statistical methods: a) logisticregression(LR),b) neural network(NN)andother
neural networkstype models(SVM’s,randomforest,decisiontree),c) genetic
algoritmmethod(GA),d) multivariate anddiscriminantanalysis(inexplanatoryphase)
e) basicdescriptivesf) informationvalue IV(x) g)
3. Validityof methodse.g. statistical testingof model and its variables:other
technical details(outliers,leverage,Mahalanobisdistance,heteroskedasticity,non-
normality,misspecificationof model).Misspecification meansthatourtestsand
distributionsare notvalidwhichleadsatworstto invalidstatisticalinference.
Inputtingmissingdatabyforexample k-meansmethodorEM-methodor
intrapolation.
4. ExplainedY (“good”,“intermediate”,and“bad” loans) and X-variables(attributes,
charasteristics of customers) used.
5. Conclusionsand results on each researchpaper presented.Reservationsto
results.
I) Rating of creditscoringin a) “good” e.g.regularlypayingcustomers=non-defaulters
b) ((fringe customers e.g. “intermediate”)) andc) non-loanedcustomerore.g. “bad”
customers=defaulters. Mostpapersdivide credit intocreditworthy and non-
creditworthy.This is a dichotomy.
II) Howevercontinuesscoringcardscanbe usedalsoandare used. These apply
thresholdand cut-offvalues for continuosranges of Y-variable/s.
III) Some papersdiscussautomatizationwithStatisticscomparedtomanual credit
decisions. Forexample Hand& Henley(1997). WhenFAST DECISION (asisthe case)
are neededthe LRor ANN algorithmprovidesthe initialdecisionINSTANTLY.These
StatisticsalgorithmandLR model decisionare usuallyHIGHLYACCURATEIN
SCREENINGDEFAULTERS and NON-CREDITWORTHYapplicants.
6. Critique ofresearch paper. (our opinion)

4. 7. Usefulness.(ouropinion) (Ourpersonal valuationof the qualityof the paperand
rating 1-5 stars (1 poor,5 excellent)).
THE RESEARCH PAPERS
A) Credit scoring – Case study indata analytics
by NikosSkantzosand NicolasCastelein at Deloitte, 2016.
1. x-data(2 categories,goodand bad loans) andy-data(2 categories,goodandbad loans)
presentedinbarchart and table.The ratioof badand good loans(B/G) is11 % and 8 % for
x1 and x2 data. For y1 it is15 % and y2 4 %.Informationvaluesare IV(x)=0.0064 and
IV(y)=0.158.Overall there are Nx1=775 obs,Nx2=325 obs,Ny1=630 obs,Ny2=470 obs.
2. Logisticregressionmultivariate (LR),IV(x)andIV(y) informationvalue.Takingintoaccount
nonlinearx-variablesandinteractionsof x-variables(x1*2,x2*2,x1*x2,….) inLR model.This
shouldbe testedusingWald,Likelihoodratiotests.
3. Ratingloandecisions=creditscoringintotwo categoriesy1=default=1,y0=non-default=0.
Splittingthe dataintoA) TRAININGDATA B) FITTINGDATA.
4. ROC-CURVEanalysis“ReceiverOperatingCharacteristic”. Predictionpowerof LRmodels.
AreaunderROC-curve > acceptable >70 % obs, 80 % obsgoodprediction,verygood> 85 %
obs.Confusionmatrix (threshold:>60 acceptable,Good> 70 %,VeryGood> 85 %).
5. Conclusionsare thatROC curve,Informationvalue(IV(x)) andConfusionmatrix with
60,70,80 % correct predictionlevelsshouldbe used.
6. ES, VS,WE SAY: 5-STAR researchpaper-> note outlieranalysisof Boxplotsandleverage.
HeteroskedasticityiswithWhite-robuststandarderrorsinregressionmodels.
7. We have nowadaysRANDOMPARAMETERLOGISTIC MODELS ANDMULTINOMIAL AND
ORDERED LOGIT REGRESSION that performmuchmore betterthanthese.STATA CAN
PROVIDETHESE !
B) Credit-scoringmodelsinthe credit unionenvironmentusingneural networks and genetic
algorithms.
V.S.Desai,D.G. Conway,J.N.Crook,G.A.OverstreetJnr,IMA Journalof Math Appsin Bus& Ind
(1997:8:323-346)
1. CreditunionsM,N, L (3 creditcompanies).Mare more or lessgeneral populationpeople.L
are teachers.N are telephone companyemployees.The sample sizesare Nm=918 obs,
Nn=853 obs,Nl=962 obs.
2. Statistical methodsare descriptive analysis(mean,median,CV),logisticregression(LR)
neural networksusingmultilayerperceptrons(CMPL) andgeneticalgoritmsfordiscriminant
analysis(GA).Neural networkarchitecture(MLP),Logisticregression(LR),lineardiscriminant
analysis(LDA),geneticanalysisof LDA.
3. Customersare “good”,“poor” and “bad” customersdependingontheirbillingpayment
habits.The aimis to classifyasmanyas possible correctlybystatistical methods.
Thismeansfor example;numberof customersobserved“good”denominatorandpredicted
numberof customers“good”nominator= (#predicted “good”/#observed “good”,%).And
observed“bad”denominatorandpredicted“bad”nominator(#predicted “bad”/#observed
“bad”,%).The percentage of relations
e.g.the class of “good” customersisdividedintotwoclassesof “good”and“poor”. A
DEFINITIONS:“good”customerhasNOpaymentsthatareoverdue31daysor more.A

5. customeris classifiedas “poor”if the paymenthasEVERbeen overduefor60 daysormore. A
“bad” customerisa customerif,atany time inthe last 48 months(4 years),eitherthe
customer’smostrecent loan i) wascharged off or the customerwent ii) bankrupt.
4. See the table forY andX-variablesbelow.Theseare justexamples.
5. ResultsforLR modelsare GOOD whenpredictingthe general populationdefaultersor“bad”
risk(CreditUnionM) byDeloitte papergivenclasses.The teacherscreditunionLisa
boundarycase (good/poorprediction) with50-60correct predictionof defaulters.Credit
unionN for telephoneworkersisaPOORpredictinginLRmodelsof defaulters.
Geneticalgorithmsprovidethe GOODpredictionof Teachers(Lcreditunion) defaulters.
MLP algoritmsof neural networksbringessential nothingnew todefaultersprediction.
The Best predictingmodel isthe GeneticAlgoritm!ThisisaMonte Carlosimulationmethod
that isadoptedfromBiostatistics.Neuralnetworksevenwithmajoradjustmentsgive no
advantage overLR in thispaper.
6. WE GIVE4-stars: ES: Oldpaper.Neural networksprovidessuprisinglylow scores.Requires
highmathematical skillsandknowledgeof thisgeneticalgorithmmethodthatworksbestin
Biostatics.Vikke asamathematiciancould evaluate thismethodbetter.
7. Overall the methodsare describedattheoretical level.Needtouse Stata,R and Python
packagesinpractice.We needtostart-upon searchingR/PythonMachine learningof Neural
Networks(NN).

9. C) Will machinelearningandhyperparameter optimizationbecomea game changerfor
credit scoring?Paper presented at the XV Conferenceon Credit Scoring,Edinburgh,
Scotland.
Authors: KnutOpdal,Rikard Bohm,ThomasHill, 2017.
1. UKCredit company dataisused.Lead acquisition information.Loan application form
information.Creditrating agency information.InternetorMobileapplication or other?
2. Logistic regression (LR) and Neuralnetwork(NN) methods.Deep-learning neuralnetwork.
3. Ratingloandecisions=creditscoring intotwo categoriesy1=default=1,y0=non-default=0.
Splittingthe datainto90 % -> A) TRAININGDATA (75 %) B) TESTING DATA (25 %) and C)
VALIDATION DATA 10%.Missingvalueswere intrapolated(extrapolated?)withstatistical
techniquesnamelyWoE.
4. 450 predictorX-candidates,N=8858 observations.“Good”loan/creditisa loan with
installment/invoicesbefore30 daysafterdue datewere defined as“Good”.“Bad” is a
loan/creditthatis installments/invoicesnotpaid within 30 daysafterduedate.The target
forloansthat still had notreached 30 daysafterdue datewere defined to be missing.
5. Goodness-of-fit== AUC-CURVE=ROC_CURVE.
Result: money earned is 8-24 % or 30 eurosper bill more(178 GBP collected per bill of NN
versus144 GBP per bill of LR) and differencebetween TOTALprediction measured by ROCis
2,6 % in favorof Optimized NeuralNetworkmodels.Thisis atthe averagebill collection level.
Every 0,1 % counts!!
6. The authorsgivelittle evidence of how they build the logistic regression modelor neural
networksthey use.Howeverthey show that3-layer deep-networksmay overfitand
“overlearn”the training dataand can not adjustto NEW ENVIRONMENT!
7. Overall this paperis 4-STAR and Good description of CAREFULLYDONE the NeuralNetwork
technology.Howeverbusinessdisclosureleavesusto do a lot ourselves.
D) Buildingcreditscoring modelsusinggenetic programming,ExpertSystems with
Applications29 (2005) 41-47
Authors:Chorng-Shyong Ong,Jin-Jeng Huang,Gwo-Hshiung Tzeng
1. Australian(N1=700) andGerman data (N2=1000) are usedwiththe followingproportion
of positive creditdecisionsN1=46%!N2=70%. Note the extremely“bad”behaving
Australiandata.
2. Logisticregression(LR) andNeural network(NN) methods.Geneticalgorithms(GA).
Non-parametricdiscriminantandK-nearestneighboranalysis.
3. Ratingloandecisions=creditscoringintotwo categoriesy1=default=1,y0=non-
default=0.X-variablesnotdescribedthatgood.Reference to“common”X-variables.
4. Splittingthe datainto 90 % -> A) training(75 %) B) testingdata(25 %) and C) validation
data 10%. Missingvalueswere intrapolated(extrapolated?)
5. Discretizationandcategorizationof continuousattributes(X).Tuningandtrainingthe
geneticalgoritm.Calculatingresultsfromall commonmethodsof creditscoring.
6. a) Highlysuprisinglythegeneric algorithmhasonly 10-15 % prediction
error withthe rather dubiousAustraliandata.The same is true for other methods. This
raises manyquestions.
b) The resultswith20-40 % predictionerrorforGermandata seemsreasonable and
easyto believe.

10. c) Thispaperpresentsmanymethodsbutthe qualityof the data ruinsitall for
Australiandata.Germandata ok.
E) Neural network credit scoringmodels,Computers& OperationsResearch 27 (2000) 1131-
1152
Author:David West
1. The data consistsof Australiandata(N=700) andGerman data (N=1000). For some
reasonthe data is describednotmuch.Howeverthe openingof the paperisvery
extensive anddescribesthe companydefaultvs.individual defaultriskaswell as
researchdone upto 21st
century.
2. Methodsinclude 5ANN-methods,LDA islineardiscriminantanalysis,LRlogistic
regression,k-nearestneighbormethod,kernel-densityestimationanddecisiontrees.
Overall MOSTcreditscoringmethodsare testedinthispaper.ThisisGood NEWS !
The Bad newsisthatthere issome concern overthe qualityof the data.
3. X-variablesare describedverywell intable 6(MUST SEE). The Y variable isthe standard
(0,1)-variable “good”riske.g.creditworthy andnotcreditworthy“bad”risk.
4. SplittingdataintoTRAININGANDTEST DATA thenusing10-runs inANN’sestimation.
5. Mixture-expertANN’sandradial-basisANN’sperformbeste.g.give BESTprediction.
LogisticregressionLRisfoundto be mostaccurate of the traditional methods.Of the
more reliable Germandataitcan be saidthat LR’s andANN’scompete “head-to-head”.
The 1950’s parametricand non-parametricmethodsdonotperformpoorlybut
traditional LDA,kernel-densitylagsignificantlybehindLRand ANN.
6. Critiqueis concerningthe data whichis kept quite candid(especiallythe Australian
data).
7. Thispaper4,5 -STARin that itdescribesthe theory,methodsandliterature extremely
well.Mustreadfor someone wantingtolearncreditscoring! Look at Germandata
results,please,thank you !

12. Note that infigure 1. above the statistical errortermsenterfromthe sidesof the hidden
and outputlayerspatternandare not mentionedforsome reason.The structure
depictedabove isone of the most simple structuresof ANN.
F) Statistical ClassificationMethodsinConsumerCreditScoring: a Review.J.R.Statistic.Soc.A
(1997), 160, Part 3, pp. 523-541.
Authors: D.J. Hand & W.E.Henley
1. Thispaperis purelyareview of literature.Itdescribesthatthe datausedincredit
scoringis usuallyN = 10 000 - 100 000 andacceptance of creditisfoundto be roughly70
% across the board.
2. The paper reviewsthe methodsavailableinthe 90’s.Of these LR = logisticregression,
LDA = LinearDiscriminantAnalysisandk-neighbourmatchingandANN e.g.neural

13. networkshave survivedbesttoourday (see:Deloittecompany,2016; West2000;
Ophdal 2017).
3. InformationcriteriaIV(x) andROC-curve introduced.These are the measuresof correct
prediction.Define also COR=# correctlypredictednumberof obs/# All observations=
correctlypredictedpercent.Then ErrorRate = 1 – COR, percent.
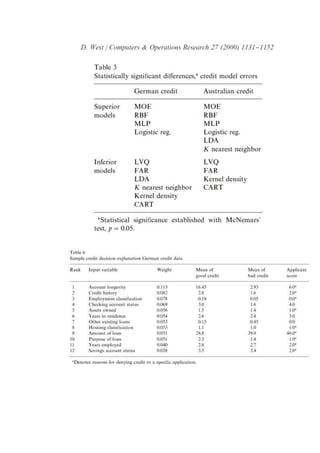
4. X-variablesare reviewedonlyalittle.The emphasisisonmethodsandreviewing90’s
literature.Backthenthe standardtechniqueswereLDA andOLS regression.Decision
tree techniquesalso.
5. Promotingk-nearestneighbormethod.The differenceiscreditscoringwithrespectLRis
howeverquite small0.68 % e.g.underone percentinN=5000 observations.Thisis35
people gettingacreditmore.The acceptance rate is70 % so 3 500 people getcredit.
The authors consider70 % a “loose criterion”andconsiderthe change incrementaldue
to populationdrift(fringe customersatstake).
6. EconomicBoomsand Busts cause populationdriftbetween“good”and“bad” creditand
changesinlegal institutionalso.Therefore inpractice we betterscore cardsor needover
1 % predictioninsmall populationsthe authorsconclude.
7. Critique:In large populationsa0,1 % issignificant(N=100 000)  100 personsgetting
credit. The authorsstart their paper with thispopulationsizebut then reduce it.
8. 3-STAR paper.Most of the techniquesare from90’s but the descriptionof a) credit
scoringand b) creditrating problemisdone inanexcellentmanner.
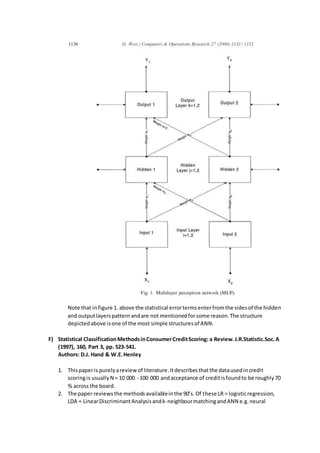
G) Comprehensible CreditScoringModelsUsingRule Extraction From
Support Vector Machines,David Martens, Bart Baesens,Tony Van Gestel,JanVanthienen,
K.U.Leuven,Dept.of DecisionSciencesand InformationManagement,
Naamsestraat 69, B-3000 Leuven,Belgium.
1. The data is Australiancreditscoringdata(N=690) and Benelux countrymid-size
companybankruptcydata (N=844). There isconcernwithAustraliandataqualityin
otherpapersinthe fieldof study.
2. The paper presentsthe “state-of-the-art”methodsthatare emergingincreditscoring
literature concerningAIandMachine Learning.These are relatedtoSupportVector
Machine algorithms(SVM’s).The authorstake accountof the complexityof these
models.Therefore theyare notevidentoreasyto presenttonon-experts.
3. Standardcorrectionof prediction(COR) percent(orErrorrate = 1 - COR percent).
4. X-variablesare lagof paymentsandsolvencyratesof companiesandbalance of
paymentsforbankruptcy.ForcreditscoringX’sare not discussedingreatdetail.Y-
variablesare probabilityof bankruptcyanddefaulting.
5. The modelsperformance iscompared.ItisfoundthatSVM-modelsperformbest
followedbyLR models.
6. Critique:dataqualitycouldbe betterforcreditscoringwithlargerthanN>>690.
7. 5-STAR paperindescribingnewest(andmostcompex) methodsinthe fieldof creditand
bankruptcyscoring.
NOTE:
“”“ Andrews,DiederichandTickle [1] propose aclassificationschemeforneural network
rule extractiontechniquesthatcaneasilybe extendedtoSVMs,andisbasedon the
followingcriteria:
1. Translucencyof the extractionalgorithmwithrespecttothe underlyingneural

14. network;
2. Expressive powerof the extractedrulesortrees;
3. Specializedtrainingregimeof the neural network;
4. Qualityof the extractedrules;
5. Algorithmiccomplexityof the extractionalgorithm.””” -quote frompaper.
H) Investigationand improvementofmulti-layerperceptronneural networks for credit scoring,
Zongyuan Zhaoa, Shuxiang Xua Byeong, HoKangbMir Md, Jahangir Kabira YunlingLiuc, Rainer
Wasingera.
School of EngineeringandICT,Universityof Tasmania,Launceston,Tasmania,Australia
School of EngineeringandICT,Universityof Tasmania,Hobart,Tasmania,Australia
College of InformationandElectrical Engineering,ChinaAgriculturalUniversity,Beijing,China.
Highlights
• TheypresentanAverage RandomChoosingmethodwhichincreases0.04 classificationaccuracy.
• InvestigatedifferentMLPmodelsandget the bestmodel withaccuracyof 87%.
• Accuracy increaseswhenthe modelhasmore hiddenneurons.
Abstract
Multi-LayerPerceptron(MLP) neural networksare widelyusedinautomaticcreditscoringsystems
withhighaccuracy and efficiency.Thispaperpresentsahigheraccuracy creditscoringmodel based
on MLP neural networksthathave beentrainedwiththe backpropagationalgorithm.Ourwork
focusesonenhancingcreditscoringmodelsinthree aspects:(i)tooptimise the datadistributionin
datasetsusinga newmethodcalledAverageRandomChoosing;(ii) tocompare effectsof training–
validation–testinstance numbers;and(iii) tofindthe mostsuitable numberof hiddenunits.We
trained34 models20 timeswithdifferentinitial weightsandtraininginstances.Eachmodel has6 to
39 hiddenunitswithone hiddenlayer.Usingthe well-knownGermancreditdatasetwe provide test
resultsanda comparisonbetweenmodels,andwe geta model withaclassification accuracyof 87%,
which is higherby 5% than the best resultreported inthe relevantliterature of recentyears. We
have alsoprovedthat ouroptimisationof datasetstructure canincrease amodel’saccuracy
significantlyincomparisonwithtraditionalmethods.Finally,we summarisethe tendencyof scoring
accuracy of modelswhenthe numberof hiddenunitsincreases.The resultsof thisworkcanbe
appliednotonlytocreditscoring,butalsoto other MLP neural networkapplications,especially
whenthe distributionof instancesinadatasetisimbalanced.
7. RECENT ANDMODERN RESEARCHPAPERWITH GOOD QUALITY DATA.THIS PAPER
COULD NOT BE OBTAINEDMORE DUE TO FEE POLICY.BEHIND MOVINGWALL.

15. I) RANDOM FOREST (DECISIONTREE = DT) MODELS BY SHARMA - SOME RESULTS
https://cran.r-project.org/doc/contrib/Sharma-CreditScoring.pdf
AndPPT-slidesetfrominternetwhere Mile worldrecordandSharma’srandomforest
calculationpresented.Canbe easilyobtainedviaGoogle.Here iskeyresulttable for
accuracy in percent.Note thatthe differencesinmodelspredictionare quite small.
The largestdifferenceis0,9 % betweenrandomforestwithinteractionandlogitwith
interactionterms.Basedona small numberof methodsobserveditisaverage quality
researchpaper(3-star).Critique:Eagerwordstomarketownmodel.
J) A betterComparison Summary of CreditScoring Classification.(IJACSA) International
Journal Of AdvancedComputer Science and Applications,Vol.8, No.7,2017. Sharjeel
Imtiaz, AllanJ. Brimicombe.
1. Data is fromTaiwanUCI website for2006. It isfinancial stressdataalso.Atthe time
there wasa banking/creditcrisisinTaiwan.Fittingthe modelsindisturbingtimes.

16. 2. ANN-1(single-layerdefaultmodel),ANN-H(minimumhiddenlayersmodel),ANN-L
(linearmodel withoutanyactivationfunction)modelsare mainmodelse.g.neural
networks.These 5hiddennodes,2hiddenlayersand19 inputparametersare tested
to findbestmodel.(gradual incrementmethod).These are comparedwithlogistic
regression (LR) withRANDOMEFFECTS(panel dataor RandomCoefficients)and
Decisiontree (DT). Decisiontreesare:default,Pruning,boosting10 %,Boosting100
%.
3. AUC-curve =(ROC-curve) andErrorrate analysis.There isfavoringof errorrate
analysisasthe authors claimthisto be a bettermethod.Imputationof missing
valueswith K-meansmethod.The errorrate is(1 - the rate correct predictionrate)
inthe data. The authorspresentactuallythe correctpredictionrate!
4. Y is standardtwo-dichotomous(0=no-default,1=default).X’sincategorical nominal
are SEX,EDUCATION,MARITAL STATUS. Categorical April toSeptember(Py_0to
Pay_6),Continuesare AGE,Amountof givencredit(Limit_BAL), Amountof bill
statement(BILL_AMT1 to BILL_AMT6), Amountof previouspayment(PAY_AMT1to
PAY_AMT6).
5. Conclusions:ANN-Lmodel ismarginallyfoundtobe the bestmodel (+0,1 % betterin
ROC,+0,2 %by Error Rate than RandomEffectsLR).Best decisiontree model is
Boosting10 %model DT-model whichis -2,67% percentworse inerror rate than
ANN-L.
6. Critique:dataisnot presentedwell (businesssecret?).
7. Usefulness:4.Quickjumpfrom introductiontoresults.Itisinterestingtosee that
whenimputingmissingvalues(K-meansprocedure)intothe datathe bestmodels
are ANN-linearandLogisticRegression.Whenno-imputationof missingvaluesdone
the bestmethodforstatistical analysisisDecisiontree with10% Boosting
technique.
CONFERENCEPAPERS
K) A CreditScoring Model Based on Alternative Mobile Data for Financial Inclusion
by Xinhai Liu,Ti Wang, Wei Ding, Yanjun Liu and Qiuyan Xu. Edinburgh credit scoringand creditcontrol
conference 2017.
1. alternative datalike mobile data. Inthe papertheyusedcall detail record(CRDR) andbilling
data. Otherpossibilitiesare payment,facility,e-commerce andsocial networkdata.They
extracted15 featuresfromthe mobile phone datatodescribe behaviorandsocioeconomic
status.The featuresare notdescribedinthe paper.The defaultof consumersisdefinedas
the 30 days past due during12 monthsperformance window.The observationtimewindow
for mobile phone behavioristhree months.Atlast,the KSvalue isaround42 in the
evaluationtest.
2. inthe papermobile phone datawasmatchedthe financial data(creditdefault) usingcross-
training.EstimationmethodisbinaryclassificationusingLR.
4. goodand bad loan.
5. paperdoesn’tshowanyresults.

17. 6. value of the paperis minimal andprovidesonlyanidea.
7. usefulness:3
L) Will machine learningand hyperparameteroptimizationbecome a game changer for credit
scoring? by Knut Opdal,Rikard Bohm and Thomas Hill.Edinburgh creditscoringand creditcontrol
conference 2017.
1. leadacquisition(channel,leadprice,other leadinfo),
data providedonthe applicationform(demographicinformation,employmentstatusand
salaryetc.),
creditinformation(Experian,Equifax,CallCredit),
other data (the method/device usedforapplication,date andtime of application)
2. machine learningalgorithms(stochasticgradientboostinganddeeplearningneural
networks) withhyperparameteroptimization.Theycomparedthese toindustrystandard
logisticregressiononWeight-OfEvidence (WoE) transformedpredictors.
3. The «last» 10% of the paid-outloanswere usedasout-of-time validationsample.Forall
analyses75% of the remainingobservationswereusedfortrainingand25% fortesting.
The trainingand testingsampleswerestratifiedbytargetanda genericscore tomake sure
the trainingsetwas representative.
4. Installment/invoicesnotpaidwithin30days afterdue date were definedas“Bad”.
Installments/invoicesbefore 30days afterdue date were definedas“Good”.The target for
loansthat still hadnotreached30 days afterdue date were definedtobe missing.
5. table 2 showsthe profitincrease inthe loanportfoliowithdifferentmethods.
6. paperconclusion:Inour example,we showedthatitwaspossible toincrease the expected
profitina portfolioby8% byusingappropriate machine learningtechniquesinsteadof the
industrystandardlogisticregression.Further,if the hyperparametersinthe machine
learningtechniques(inthiscase BoostingTrees) were furtherfine-tuned(optimized),itwas
possible toincrease the profitby24 % comparedtologisticregression.These techniques

18. have potential tobe a game changer,but we believemanybankswill continue touse logistic
regressionasbefore,andtherefore we donotbelieve thatitwill have abigenoughimpact
to qualifytobe calleda game changer.On the otherside,we dobelievethatthere will be
banksthat will embrace these methodsandbe able toproduce scorecardswithhigher
performance.These bankswill be more competitive andincrease theirprofit.We therefore
thinkthese methodswill playanimportantrole forthe bankingsectorinthe time tocome.
7. Usefulness:4
M) Piecewise LogisticRegression:anApplicationin CreditScoring,
by Raymond Anderson, Standard Bank of South Africa,Edinburgh credit scoringand creditcontrol
conference 2015.
1. high-riskportfolio,where riskappetite hadbeenreinedinsubstantiallyoverthe period
underconsideration.
2. Piecewise LR
3. There are three casesthat we will be comparingin thispaper,all of whichuse the weightsof
evidence:
a. Base Case,whichreferstothe standardapproachfor logisticregression,withone
variable percharacteristic;
b. Piecewise,where there maybe one ormore variables(pieces)forthe characteristic,
where each“piece”mayrepresentone ormore coarse classes;
c. Dummy,where there isaseparate variable (piece) foreachcoarse class,each
containingthe weightof evidence if the characteristiciswithinthe group,andzeroif
not
5. The resultsof thisanalysisindicate thatbettercreditscoringmodelscanbe builtusing
piecewise logisticregressionthanthe same regressionusingasingle variableper
characteristic(Base Case) orattribute (Dummy).The Gini coefficientsare higher,whilethe
correlationsandvariance inflationfactorsare lower.Atthe same time,the modelsare more
robust,beingbetterable tohandle achangingriskenvironment.
In the current instance,we are lookingsolelyatlogisticregression.Althoughthe typical uses
of WOE and dummieshave beenpresentedabove,theycanbe andare usedincombination
inlogisticregression.Itisonlythe variable “x”valuesthatchange dependinguponhow the
variable hasbeentransformed.
7. usefulness:2

19. N) Creditscoring,statistical techniques,and evaluationcriteria: a review of the literature.
IntelligentsystemsandAccounting, Finance & Management,2011, 18 (2-3) pp. 59-88.
Authors:Abdou.H.,PointonJ.
1. Data isliterature review dataof 214 articles.Most articlesdatais confinedtoN=1 000 –
10 000 observationsdata.There are few creditscoringpaperswithoverN > 10 000 customers.
Thisis due to the limitationof academicwriterstogetprivate companydata. SELECTION BIAS is
always presentbecause we don’t know of the people who we don’t give credit to. We have to
getthisdata from Asiakastieto(creditunionrater) orsome otherratingagency.
2. All relevantstatistical methodsin the literature.IncludingANN,K-nearestneighbor,Markov
chains,Decisiontrees(DT),GenericalgorithmsGA,RandomForestsalgorithms,Logisticand
ProbitregressionLR,OLS,discriminantLDA,kernerfuntions,COXHAZARDregression,
multivariate methods,non-parametricdecisiontrees(DT).
Result:NO UNIVERSAL BEST METHOD EXISTS. Alwaysdivide datainto1) training2) testingand
3) validationparts.ThenPILOTyourresultsbefore usingtheminreal-worldsituations.Compare
the resultsof at least2 to 3 DIFFERENT STATISTICALORMATHEMATICAL METHODS.
3. Meters,“goodness-of-fit”:ACCrating(average creditscoredright),ROC-curve rating,
Confusionmatrix,Type IIerror,Type Ierror, Costof misspecification,Errorrate.
4. Y-variablesare lineartestscore measure ordiscrete (2-classor3-class) classificationof
creditscore into “good”,“intermediate” and“bad” risks.The dangerof neglectingpeople
withsome delaysintheirpaymentbuttakingcare of theirloansisWARNED about.There is
profitmarginhere thata simplistic“black-white”classificationof creditworthy“the goods”
and uncreditworthy“the bads”presents.Inreality there isscope for a “gray”-area where
paymentsmaybe (abit) late orneedsome (minorcost) arrangement.Thisispointedoutby
the authors as improvingourmodels.
X-variablesare: age,marital status,dependents,havingatelephone,havinghome
mortgage,havingcar loan,havinga creditcard, numberof creditcards, total amountof
credit,total amountof income,loanduration,education,occupation,yearinwork,time at
presentaddress,postal code,bankaccounts,numberof bankaccounts,purpose of loan,
guarantees.UsuallyX-variablesusedincategorical variables,butnumbercrunchallows
continuity!!
5. The resultsare that there isno “one-fits-all”methodof statisticsormathematicsthatworks
inall situations,countries,environments,economies,culturesetc.Alsoexpertopinion
shouldnotbe discountedorrebuffedwhenstatisticalmodelsare built.The FIN,SWE,NOR,
DEN environmentsare different.
6. Critique:once again the qualityof dataisnot adequate andsmall sample resultsare usedto
infermanythings.Whensample size increase thenANN andLRmethodsare marginally
differentorequal good-in-fit.We alwayshave totryout several methodsandcompare
results.
7. Useful:5. Like saidthe authorshave done a tremendousjobof goingthrough 214 articles.

20. O) Survival analysis in CreditScoring – A framework for PD estimation
Author:R. Man, RabobankInternational,2014-09-05
1. Data ishighqualitybankruptcydataand large with877 defaults.There are thousandsof
observations.B2Cdataon retail n=16383. SME corporate bankruptcydatan=14953. Simulated
data n=1000. Modelsare calculatedfor0-1 year,0-2 yearand 0-3 year risk.
2. Methodsincludedare Survival analysiswithKaplan-Meierhazard,Cox-proportionalhazard
models(PH),Weibull modelsof hazards,logisticregressionanalysis.WoE(weightof evidence)-
estimatorof discriminatorypowerbetween“good” and“bad” loans.There isa LOT of
descriptionof “How-to-Do-IT”.Thismeansthere isagooddescriptionof methodsindetail.
3. Goodnessof fitis measuredbyROC-curve.InformationvalueIV(x).Goodrate &Bad rate of
loanspredictedright.WoEscore.
4. Y1 variable isthe “time to default”indays,weeks,hours,months.The betteraccuracythe
better.These are forecastedbysurvival modelsthathave proportionalornon-linearhazard
curves.EvenATF – acceleratedfailure timemodels.h(t) =hazardfunction,S(t)=survival function.
The Y2 variable isalsojust 1=defaultor 0=survival.The resultsof differentmodelsare compared.
Logistictransformation,Logranktransformation,Statistical Optimal Approach(Seepage 49).
X-variablesare discussedindetail.Theyvaryfromconsumertobusinessdata.See appendix.
5. The resultsare that survival modelsdowell inpredictingbankruptcyratesfordifferenttime
periods.Furthermore itispossible toforecastfuture bankruptciesbasedonhistorical dataat
differenttime intervals.These are the advantagesof survival analysis.
6. Critique:toomuchtime andeffortisput onidentifyingx-variablesclasses.We shoulduse
more continuesvariablesinthe future because computingpowerpermitsthiswell !
7. RabobankpaperwhichusesBigData andstandard LR and PH methods.Must read!
P) EM-procedure, Stata, irt pcm — Partial creditmodel.
I) irt pcm fitspartial creditmodels(PCMs) toordinal items.Inthe PCM,itemsvaryin
theirdifficultybutshare the same discriminationparameter.irtgpcmfitsgeneralizedpartial
creditmodels(GPCMs) toordinal items.Inthe GPCM, all itemsvaryintheirdifficultyand
discrimination.
Quickstart
PCMfor ordinal itemso1to o5
irt pcm o1-o5
PlotCCCsfor o1
irtgraphicc o1
Menu
Statistics> IRT (itemresponse theory)
Page 105., Stata IC 14.2 manual.
II)irtpcm postestimation — Postestimationtoolsforirtpcm
The followingpostestimationcommandsare of special interestafterirtpcmand irtgpcm:
CommandDescription

21. estatreportreport estimatedIRTparameters
irtgraphicc plotitem characteristiccurve (ICC)
irtgraphiif plotiteminformationfunction(IIF)
irtgraphtcc plottestcharacteristiccurve (TCC)
irtgraphtif plottest informationfunction(TIF)
The followingstandardpostestimationcommandsare alsoavailable:
Command Description
estatic Akaike’sandSchwarz’sBayesianinformationcriteria(AICandBIC)
estatsummarize summarystatisticsforthe estimationsample
estatvce variance–covariance matrix of the estimators(VCE)
estat(svy) postestimationstatisticsforsurveydata
estimatescatalogingestimationresults
lincompointestimates,standarderrors,testing,andinference forlinear
combinationsof coefficients
lrtestlikelihood-ratiotest
nlcompointestimates,standarderrors,testing,andinference fornonlinear
combinationsof coefficients
predictpredictions
predictnl pointestimates,standarderrors,testing,andinference forgeneralized
predictions
testWald testsof simple andcomposite linearhypotheses
testnl Waldtestsof nonlinearhypotheses
lrtestis not appropriate withsvyestimationresults.
Page 115, Stata 14.2 IC manual.