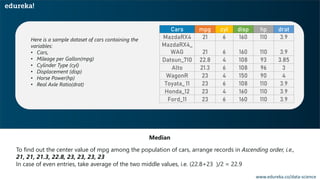
Here are the steps to calculate the standard deviation of the numbers:
1) Find the mean (average) of the numbers: (9 + 2 + 5 + ... + 10 + 9 + 6 + 9 + 4) / 20 = 7
2) For each number, subtract the mean and square the result:
(9 - 7)2 = 4
(2 - 7)2 = 49
...
(4 - 7)2 = 9
3) Sum all the squared differences: 4 + 49 + ... + 9 = S
4) Divide the sum by the number of values minus 1: S / (20 - 1)
5) Take the square root. This is the standard








































































![www.edureka.co/data-science
The Normal Distribution is a probability distribution that associates the normal random variable X with a
cumulative probability
Y = [ 1/σ * sqrt(2π) ] * e -(x - μ)2/2σ2
Where,
•X is a normal random variable
•μ is the mean and
•σ is the standard deviation
Note: Normal Random variable is variable with mean at 0 and variance equal to 1](https://image.slidesharecdn.com/statisticsandprobability-190926125156/85/Statistics-And-Probability-Tutorial-Statistics-And-Probability-for-Data-Science-Edureka-74-320.jpg)











































