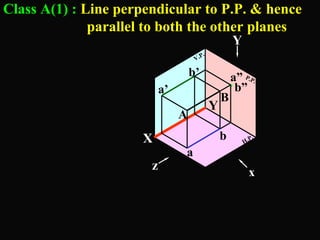
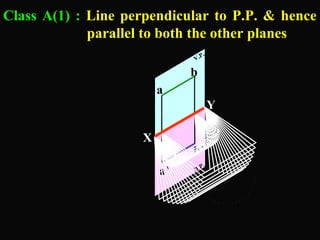
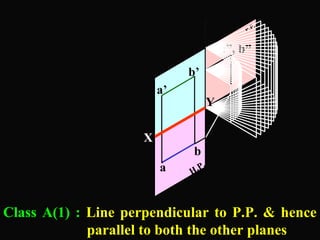
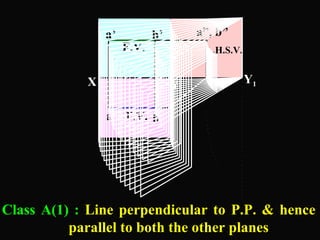
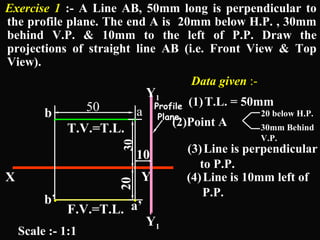
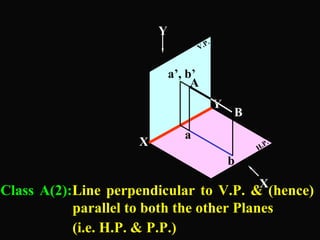
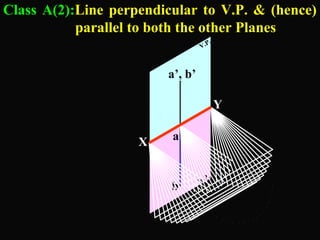
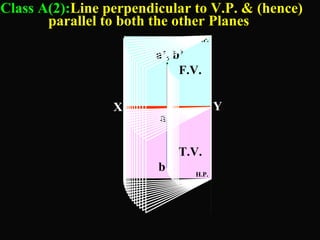
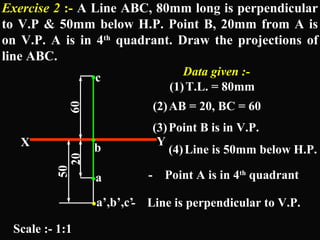
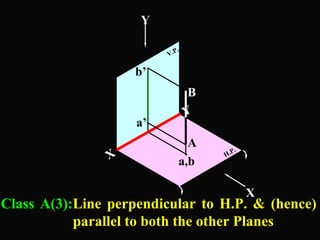
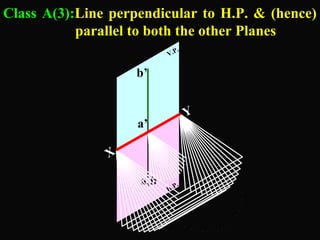
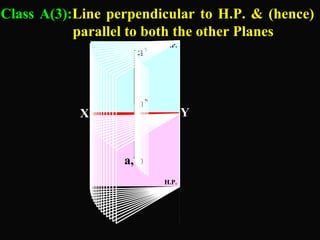
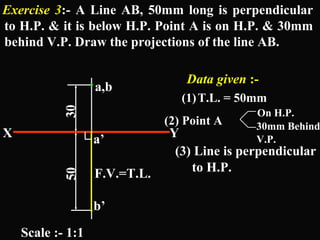
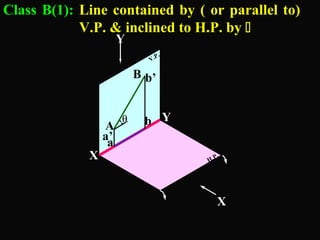
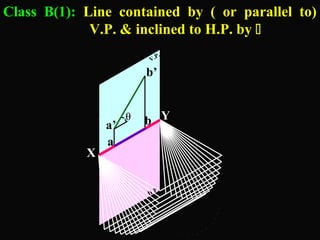
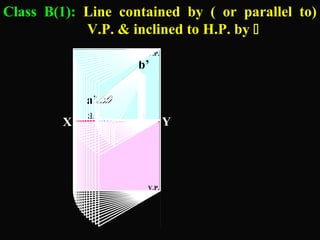
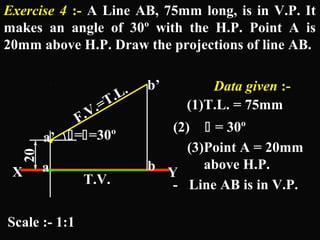
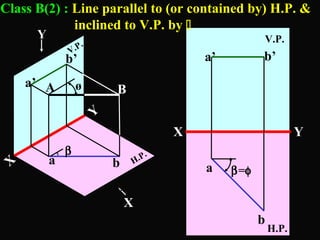
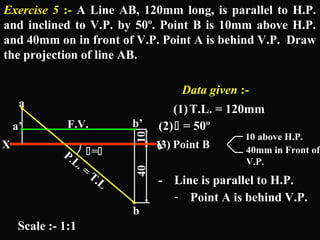
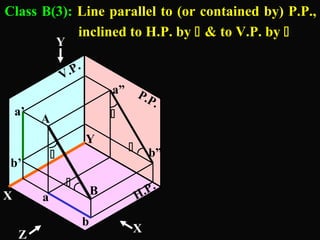
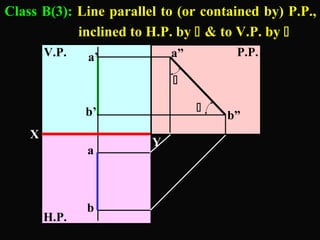
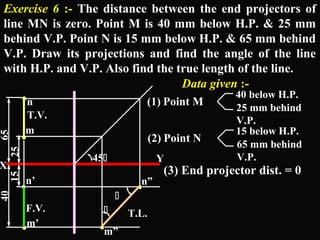
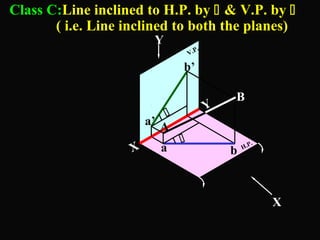
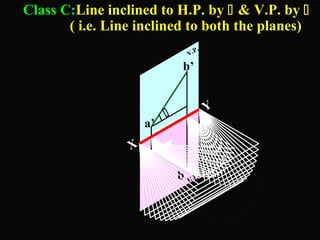
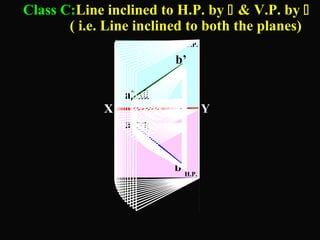
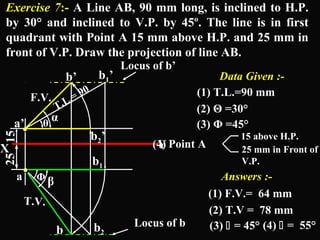
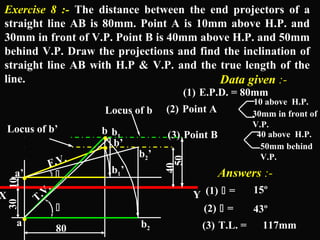
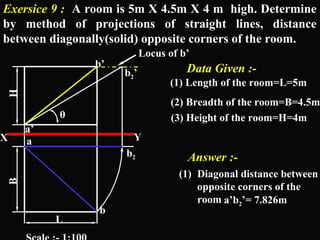
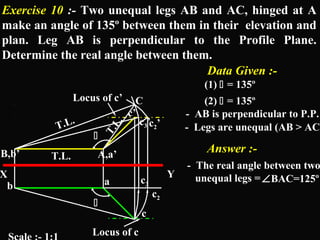
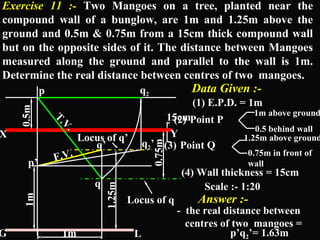
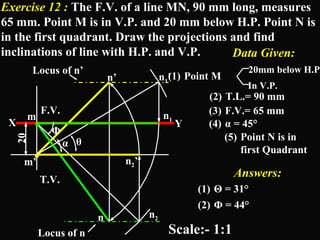
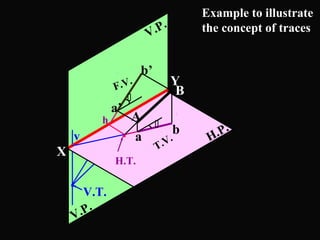
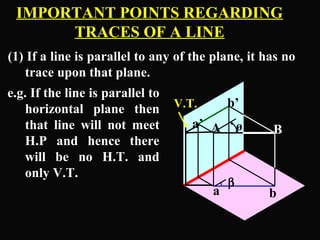
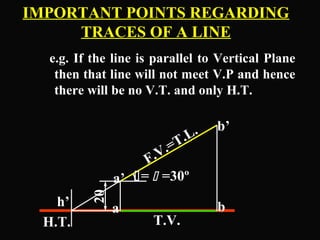
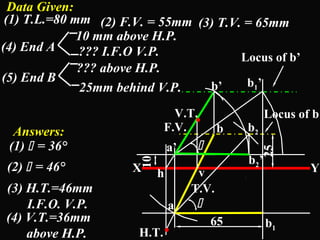
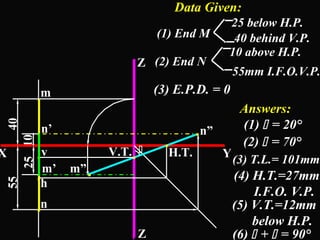
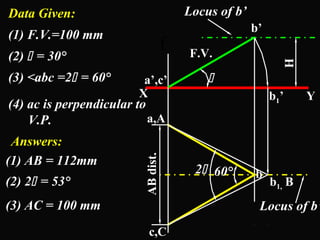
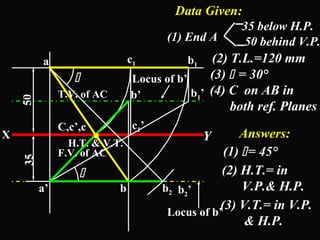
The document discusses projections of straight lines. It defines a straight line and explains that the top and front views of a straight line are also straight lines. It describes different positions a line may have with respect to the horizontal and vertical planes, such as perpendicular, parallel or inclined. Notations used for dimensions of the line are also defined, such as true length, front view length, and inclinations. Different classes of line positions are described, including lines perpendicular or parallel to reference planes or inclined to multiple planes. Examples are given to demonstrate how to draw projections of lines in different positions.

2. PROJECTIONS OF STRAIGHT LINES
Definition of Straight line:
A straight line is the shortest distance
between two points.
-Top views of two end points of a straight
line, when joined, give the top view of
the straight line.
-Front views of the two end points of a
straight line, when joined, give the front
view of the straight line.
-Both the above projections are straight
lines.

3. Orientation of Straight Line in Space
- A line in space may be parallel,
perpendicular or inclined to either the H.P.
or V.P. or both.
- It may be in one or both the reference
Planes.
- Line ends may be in different Quadrants.
- Position of Straight Line in space can be
fixed by various combinations of data like
distance of its end points from reference
planes, inclinations of the line with the
reference planes, distance between end
projectors of the line etc.

4. Notatioans used for Straight Line
True length of the line:
Denoted by Capital letters. e.g. AB=100 mm,
means that true length of the line is 100 mm.
Front View Length:
Denoted by small letters. e.g. a’b’=70 mm,
means that Front View Length is 70 mm.
Top View Length:
Denoted by small letters. e.g. ab=80 mm,
means that Top View Length is 80 mm.
Inclination of True Length of Line with H.P.:
It is denoted by θ. e.g. Inclination of the line
with H.P. (or Ground) is given as 30º means
that θ = 30º.

5. Inclination of True Length of Line with V.P.:
It is denoted by Φ. e.g. Inclination of the line
with V.P. is given as 40º means that Φ = 40º.
Inclination of Front View Length with XY :
It is denoted by α. e.g. Inclination of the Front
View of the line with XY is given as 50º means
that α = 50º.
Inclination of Top View Length with XY :
It is denoted by β. e.g. Inclination of the Top
View of the line with XY is given as 30º means
that β = 30º.
End Projector Distance:
It is the distance between two projectors
passing through end points of F.V. & T.V.
measured parallel to XY line.

6. Line in Different Positions with
respect to H.P. & V.P.
CLASS A: Line perpendicular to (or in) one
reference plane & hence parallel to
both the other planes
(1) Line perpendicular to P.P. & (hence) parallel
to both H.P. & V.P.
(2) Line perpendicular to V.P. & (hence) parallel
to both H.P. & P.P.
(3) Line perpendicular to H.P. & (hence) parallel
to both V.P. & P.P.

7. Line in Different Positions with
respect to H.P. & V.P.
CLASS B: Line parallel to (or in) one
reference plane & inclined to other
two planes
(1) Line parallel to ( or in) V.P. & inclined to H.P.
by .
(2) Line parallel to ( or in) H.P. & inclined to V.P.
by .
(3) Line parallel to ( or in) P.P. & inclined to H.P.
by  & V.P. by .

8. Line in Different Positions with
respect to H.P. & V.P.
CLASS C: Line inclined to all three reference
planes ( Oblique lines )
Line inclined to H.P. by , to V.P. by  and also
inclined to profile plane.

9. Class A(1) : Line perpendicular to P.P. & hence
parallel to both the other planes
Y
a”
P.P.
.
H.P.
V.P.
Y
X
B
A
a’
b’
b
a
b”
z x

10. Class A(1) : Line perpendicular to P.P. & hence
parallel to both the other planes
X
Y
a’
V.P.
b’
H.P.
a
b

11. P.P.
a”, b”
Y1
.
V.P.
H.P.
a’
b’
a
b
X
Y
Class A(1) : Line perpendicular to P.P. & hence
parallel to both the other planes

12. a’ b’
F.V. L.H.S.V.
a b
a”, b”
.
X Y1
T.V.
Y
Class A(1) : Line perpendicular to P.P. & hence
parallel to both the other planes

13. Exercise 1 :- A Line AB, 50mm long is perpendicular to
the profile plane. The end A is 20mm below H.P. , 30mm
behind V.P. & 10mm to the left of P.P. Draw the
projections of straight line AB (i.e. Front View & Top
View).
b . .
30
Y1
X Y
Profile
Plane
20
a’
.
b’
a
T.V.=T.L.
F.V.=T.L.
10
Y1
50
Data given :-
(1)T.L. = 50mm
(2)Point A
20 below H.P.
30mm Behind
V.P.
(3)Line is perpendicular
to P.P.
(4)Line is 10mm left of
P.P.
Scale :- 1:1
.

14. V.P.
H.P.
Y
X
a’,. b’
A
B
b
a
Y
Class A(2):Line perpendicular to V.P. &X (hence)
parallel to both the other Planes
(i.e. H.P. & P.P.)

15. Class A(2):Line perpendicular to V.P. & (hence)
parallel to both the other Planes
a’, b’
X
Y
V.P.
H.P.
a
b
.

16. Class A(2):Line perpendicular to V.P. & (hence)
parallel to both the other Planes
V.P.
F.V.
H.P.
a’, b’
X Y
a
b
T.V.
.

17. Exercise 2 :- A Line ABC, 80mm long is perpendicular
to V.P & 50mm below H.P. Point B, 20mm from A is
on V.P. A is in 4th quadrant. Draw the projections of
line ABC.
c
.
b
50 a
.
a’,b’,c’
20 60
X Y
Data given :-
(1)T.L. = 80mm
(3)Point B is in V.P.
(4)Line is 50mm below H.P.
- Line is perpendicular to V.P.
Scale :- 1:1
(2)AB = 20, BC = 60
- Point A is in 4th quadrant
.
.

18. H.P.
Y X
.
V.P.
B
A
a,b
b’
a’
X
Y
Class A(3):Line perpendicular to H.P. & (hence)
parallel to both the other Planes

19. Class A(3):Line perpendicular to H.P. & (hence)
parallel to both the other Planes
b’
Y X
a.,b
V.P.
H.P.
a’

20. Class A(3):Line perpendicular to H.P. & (hence)
parallel to both the other Planes
a’
b’
V.P.
X Y
a,. b
H.P.

21. Exercise 3:- A Line AB, 50mm long is perpendicular
to H.P. & it is below H.P. Point A is on H.P. & 30mm
behind V.P. Draw the projections of the line AB.
a,b
.
X Y
a’
F.V.=T.L.
b’
30 50
Data given :-
(1)T.L. = 50mm
(2) Point A On H.P.
30mm Behind
V.P.
(3) Line is perpendicular
to H.P.
Scale :- 1:1
.
.

22. Class B(1): Line contained by ( or parallel to)
V.P. & inclined to H.P. by 
H.P.
V.P.
a’
b’
X
Y
a
b
X
Y
A
B
θθ

23. Class B(1): Line contained by ( or parallel to)
V.P. & inclined to H.P. by 
Y
X
V.P.
b’
a’
a
θθ b
H.P.

24. Class B(1): Line contained by ( or parallel to)
V.P. & inclined to H.P. by 
b’
V.P.
a’
a b
V.P.
θθ
X Y

25. Exercise 4 :- A Line AB, 75mm long, is in V.P. It
makes an angle of 30º with the H.P. Point A is
20mm above H.P. Draw the projections of line AB.
20
F.V.=T.L.
==30º
b’
.
a’
a b
X T.V. Y
Data given :-
(1)T.L. = 75mm
Scale :- 1:1
(2)  = 30º
(3)Point A = 20mm
above H.P.
- Line AB is in V.P.
.

26. Class B(2) : Line parallel to (or contained by) H.P. &
V.P.
b’ a’ b’
H.P.
a’ A B
V.P.
H.P.
b=f
a b
a
b
X
Y
ø
X Y
b
X
Y
inclined to V.P. by 

27. Exercise 5 :- A Line AB, 120mm long, is parallel to H.P.
and inclined to V.P. by 50º. Point B is 10mm above H.P.
and 40mm on in front of V.P. Point A is behind V.P. Draw
the projection of line AB.
. .
a’ b’
10
a
F.V.
X Y
b
=
P.L. = T.L
40
Data given :-
(1)T.L. = 120mm
(3) Point B 10 above H.P.
40mm in Front of
V.P.
- Line is parallel to H.P.
- Point A is behind V.P.
Scale :- 1:1
(2)  = 50º
.
.

28. Class B(3): Line parallel to (or contained by) P.P.,
inclined to H.P. by  & to V.P. by 
H.P.
V.P.
P.P.
Y
a’
b’
X
A
B
a”
 b”

Y
b
a


Z X

29. Class B(3): Line parallel to (or contained by) P.P.,
V.P.
H.P.
inclined to H.P. by  & to V.P. by 
P.P.


a’
b’
X Y
a
b
b”
a”

30. Exercise 6 :- The distance between the end projectors of
line MN is zero. Point M is 40 mm below H.P. & 25 mm
behind V.P. Point N is 15 mm below H.P. & 65 mm behind
V.P. Draw its projections and find the angle of the line
with H.P. and V.P. Also find the true length of the line.
Data given :-
(1) Point M 40 below H.P.
25 mm behind
V.P.
(2) Point N 15 below H.P.
65 mm behind
V.P.
.
n
..
65
m
45
X Y
..
(3) End projector dist. = 0 .
F.V. 
T.L.
..
..
25
15
40
n’
m’

n”
m”
T.V.

31. Class C:Line inclined to H.P. by  & V.P. by 
( i.e. Line inclined to both the planes)
H.P.
V.P.
X Y
a b
a’
b’


Y
X
B
A

32. Class C:Line inclined to H.P. by  & V.P. by 
( i.e. Line inclined to both the planes)
V.P.
X Y
a
b

H.P.

a’
b’

33. Class C:Line inclined to H.P. by  & V.P. by 
( i.e. Line inclined to both the planes)
V.P.
b’
X Y
a 
b
H.P.
a’ 

34. Exercise 7:- A Line AB, 90 mm long, is inclined to H.P.
by 30° and inclined to V.P. by 45º. The line is in first
quadrant with Point A 15 mm above H.P. and 25 mm in
front of V.P. Draw the projection of line AB.
25 15
Φ
α
β
..
a’
a
b’ b1’
X Y
b b2
θ
Locus of b’
Locus of b
Data Given :-
(1) T.L.=90 mm
(2) Θ =30°
(3) Φ =45°
(4) Point A 15 above H.P.
25 mm in Front of
V.P.
F.V.
T.V.
Answers :-
(1) F.V.= 64 mm
(2) T.V = 78 mm
(3)  = 45° (4)  = 55°
T.L.= 90
b2’
b1 ..

35. Exercise 8 :- The distance between the end projectors of a
straight line AB is 80mm. Point A is 10mm above H.P. and
30mm in front of V.P. Point B is 40mm above H.P. and 50mm
behind V.P. Draw the projections and find the inclination of
straight line AB with H.P & V.P. and the true length of the
line. Data given :-
(1) E.P.D. = 80mm
(2) Point A 10 above H.P.
(3) Point B 40 above H.P.
50mm behind
V.P.
. Locus of b’ .
a’
Locus of b
 Answers :-
X Y
30mm in front of
V.P.
80 30 10 a
b1 b
40
50
b’
b2’

(1)  =
(2)  =
(3) T.L. =
15º
43º
117mm
.
.
b2
b1’
F.V.
T.V.

36. Exersice 9 : A room is 5m X 4.5m X 4 m high. Determine
by method of projections of straight lines, distance
between diagonally(solid) opposite corners of the room.
b2’
H B
b’
a’
a
X Y
b
L
Data Given :-
(1) Length of the room=L=5m
(2) Breadth of the room=B=4.5m
(3) Height of the room=H=4m
Answer :-
(1) Diagonal distance between
opposite corners of the
room
a’b2’= 7.826m
Scale :- 1:100
b2
Locus of b’
θ

37. Exercise 10 :- Two unequal legs AB and AC, hinged at A
make an angle of 135º between them in their elevation and
plan. Leg AB is perpendicular to the Profile Plane.
Determine the real angle between them. Data Given :-
C
c2’
(1)  = 135º
(2)  = 135º
- AB is perpendicular to P.P.
- Legs are unequal (AB > AC)
Answer :-
- The real angle between two
unequal legs = ÐBAC=125º

B,b’ A,a’
b a
c
c’
X Y

Scale :- 1:1 Locus of c
c3’
Locus of c’
c2
c3
T.L.
T.L.
T.L.

38. Exercise 11 :- Two Mangoes on a tree, planted near the
compound wall of a bunglow, are 1m and 1.25m above the
ground and 0.5m & 0.75m from a 15cm thick compound wall
but on the opposite sides of it. The distance between Mangoes
measured along the ground and parallel to the wall is 1m.
Determine the real distance between centres of two mangoes.
1m 0.5m
Locus of q’
q2
q’
q’ F.V.
21.25m
15cm
(3) Point Q
0.75m
T.V.
q
p’
p
(2) Point P 1m above ground
X Y
Locus of q
G L
Data Given :-
(1) E.P.D. = 1m
0.5 behind wall
1.25m above ground
0.75m in front of
wall
(4) Wall thickness = 15cm
Scale :- 1:20
Answer :-
- the real distance between
centres of two mangoes =
p’q21m ’= 1.63m

39. Exercise 12 : The F.V. of a line MN, 90 mm long, measures
65 mm. Point M is in V.P. and 20 mm below H.P. Point N is
in the first quadrant. Draw the projections and find
inclinations of line with H.P. and V.P. Data Given:
(1) Point M 20mm below H.P.
In V.P.
(2) T.L.= 90 mm
(3) F.V.= 65 mm
(4) α = 45°
(5) Point N is in
first Quadrant
Locus of n’
.
F.V.
.
m
X Y
20
m’
n’ n1’
n1
n2
n2’
n
θ
Answers:
(1) Θ = 31°
(2) Φ = 44°
Φ
T.V.
α
Locus of n
Scale:- 1:1

40. TRACES OF A LINE
Definition: When a line is inclined to a plane, it
will meet that plane, produced if
necessary. The point where the line or
line produced meets the plane is called
trace.
Horizontal Trace: The point of intersection of
the inclined line with the H.P. is called
Horizontal Trace or simply H.T.
Vertical Trace: The point of intersection of the
inclined line with the V.P. is called
Vertical Trace or simply V.T.

41. V.P.
.
b’
a b
H.P.
.
V.P. a’
B
A
Y
X
Example to illustrate
the concept of traces


F.V.
T.V.
H.T.
h
v
V.T.

42. IMPORTANT POINTS REGARDING
TRACES OF A LINE
- If a line is inclined to both H.P. & V.P. then
its Front view, h’ and V.T. must be on the
same straight line.
e.g. if front view of a line AB is a’b’, then
h,a’,b’ and V.T. must be on a same straight
line.
- If a line is inclined to both H.P. & V.P. then
its Top view, v and H.T. must be on the same
straight line.
e.g. if Top View of a line AB is ab, then v, a, b
and H.T. must be on a same straight line.

43. IMPORTANT POINTS REGARDING
TRACES OF A LINE
(1) If a line is parallel to any of the plane, it has no
trace upon that plane.
e.g. If the line is parallel to
V.P.
horizontal plane then
that line will not meet
H.P and hence there
will be no H.T. and
only V.T.
H.P.
a’,. b’
A
B
b
a
V.T.
Y

44. IMPORTANT POINTS REGARDING
TRACES OF A LINE
(1) If a line is parallel to any of the plane, it has no
trace upon that plane.
e.g. If the line is parallel to
horizontal plane then
V.T.
b’
that line will not meet
a’ A ø
B
H.P and hence there
will be no H.T. and
only V.T.
b
a b
.

45. IMPORTANT POINTS REGARDING
TRACES OF A LINE
e.g. If the line is parallel to
Vertical Plane then
that line will not meet
V.P and hence there
will be no V.T. and
only H.T.
V.P.
B
b’
Y X
H.P.
.
A
a,b
a’
H.T.

46. IMPORTANT POINTS REGARDING
TRACES OF A LINE
e.g. If the line is parallel to Vertical Plane
then that line will not meet V.P and hence
there will be no V.T. and only H.T.
20
F.V.=T.L.
=  =30º
b’
a’
a b
T.V.
h’
H.T.

47. Exercise 13 : A line AB, 80 mm long is seen as
a straight line of length 55mm in its front
view and of length 65 mm in its top view.
Its end A is 10 mm above H.P. & is in first
quadrant where as end B is 25 mm behind
V.P. and is in Second Quadrant. Draw its
projections and find out its inclinations
with H.P. & V.P. and also locate its traces.

48. Data Given:
(1) T.L.=80 mm (2) F.V. = 55mm (3) T.V. = 65mm
(4) End A
10 mm above H.P.
??? I.F.O V.P.
(5) End B
??? above H.P.
25mm behind V.P.
b’
b
Locus of b’
Locus of b
b1’
25
F.V.
b2
X Y
b1 65
H.T.
a
V.T.
v
T.V.
10
a’
.
.
b2’
h
Answers:
(1)  = 36°
(2)  = 46°
(3) H.T.=46mm
I.F.O. V.P.
(4) V.T.=36mm
above H.P.



49. Exercise 14 : The end projectors distance of a
line MN is zero. Its end M is 25mm below
H.P. & 40mm behind V.P. where as end N
is 10 above H.P. & 55mm in front of V.P.
Draw its projections and find out its
inclinations with H.P. & V.P. and also
locate its traces.

50. .
m
.
n’
.
v
40
10
25
m’
.
.
.
V.T. H.T.
X Y
n
n”
m”
Z
Z
h
55
. .
Data Given:
(1) End M
25 below H.P.
40 behind V.P.
(2) End N
10 above H.P.
55mm I.F.O.V.P.
(3) E.P.D. = 0
Answers:
(1)  = 20°
(2)  = 70°
(4) H.T.=27mm
(3) T.L.= 101mm
I.F.O. V.P.
(5) V.T.=12mm
below H.P.
..

(6)  +  = 90°

51. Exercise 15 : A divider instrument of a compass box
having two equal arms AB & BC hinged at B is kept
in H.P. on its needle point A & C with the line
joining A & C is perpendicular to V.P. It is seen in
front view as a straight line 100mm long inclined at
30° to H.P. while it is seen in top view as an angle abc
with <abc = 60°. Draw its front view and top view
and find;
(1) The height of point B above H.P.
(2) The apart distance between the needle points
A & C
(3)The lengths of arms AB & BC with real
between them

52. Data Given:
(1) F.V.=100 mm f (2)  = 30°
(3) <abc =2 = 60°
(4) ac is perpendicular to
a’,c’
V.P. a,A
c,C
H
b1’
b1, B
b’
Locus of b’
F.V.

X Y
2 60°
b
Locus of b’
AB dist.
Answers:
(1) AB = 112mm
(2) 2 = 53°
(3) AC = 100 mm

53. Exercise 16 : The end A of a straight line AB,
120mm long, is 50 mm behind V.P. & 35 mm
below H.P. The line is inclined to H.P. by 30°
& has a point C on it in both the reference
planes. Draw the projections of the line and
find out its inclinations with V.P. Also locate
its traces.

54. Data Given:
(1) End A
35 below H.P.
50 behind V.P.
(2) T.L.=120 mm
(3)  = 30°
(4) C on AB in
both ref. Planes
Answers:
(1)  = 45°
(2) H.T.= in
a

b1
.
Locus of b’
T.V. of AC
H.T. & V.T. .
X Y
& H.P. 35
V.P.& H.P.
(3) V.T.= in V.P.
a’
b
b’
C,c’,c
c1
50
b2
c1’
b1’
b2’
. 
Locus of b’
F.V. of AC

55. PROJECTIONS
OF STRAIGHT
LINES