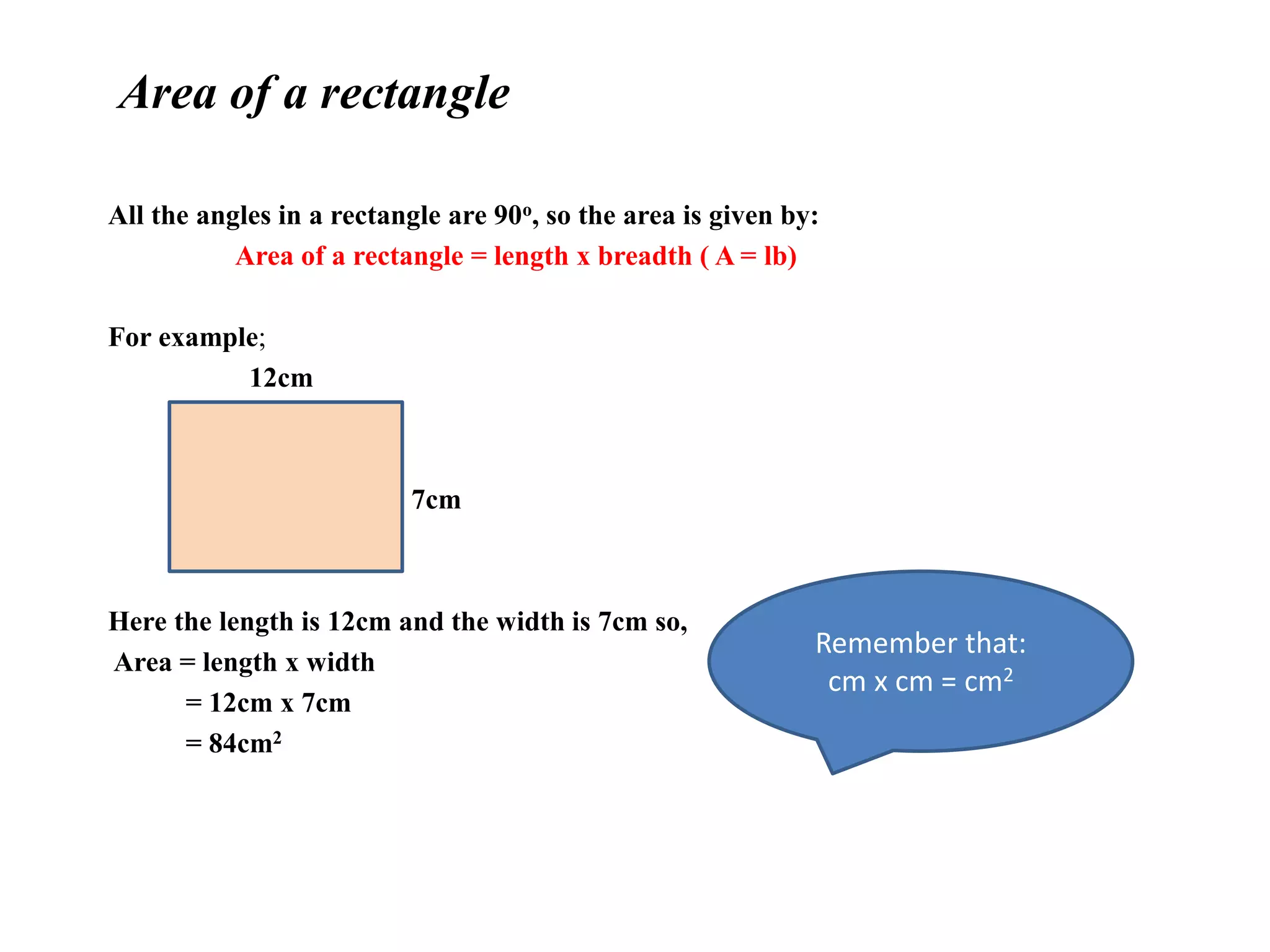
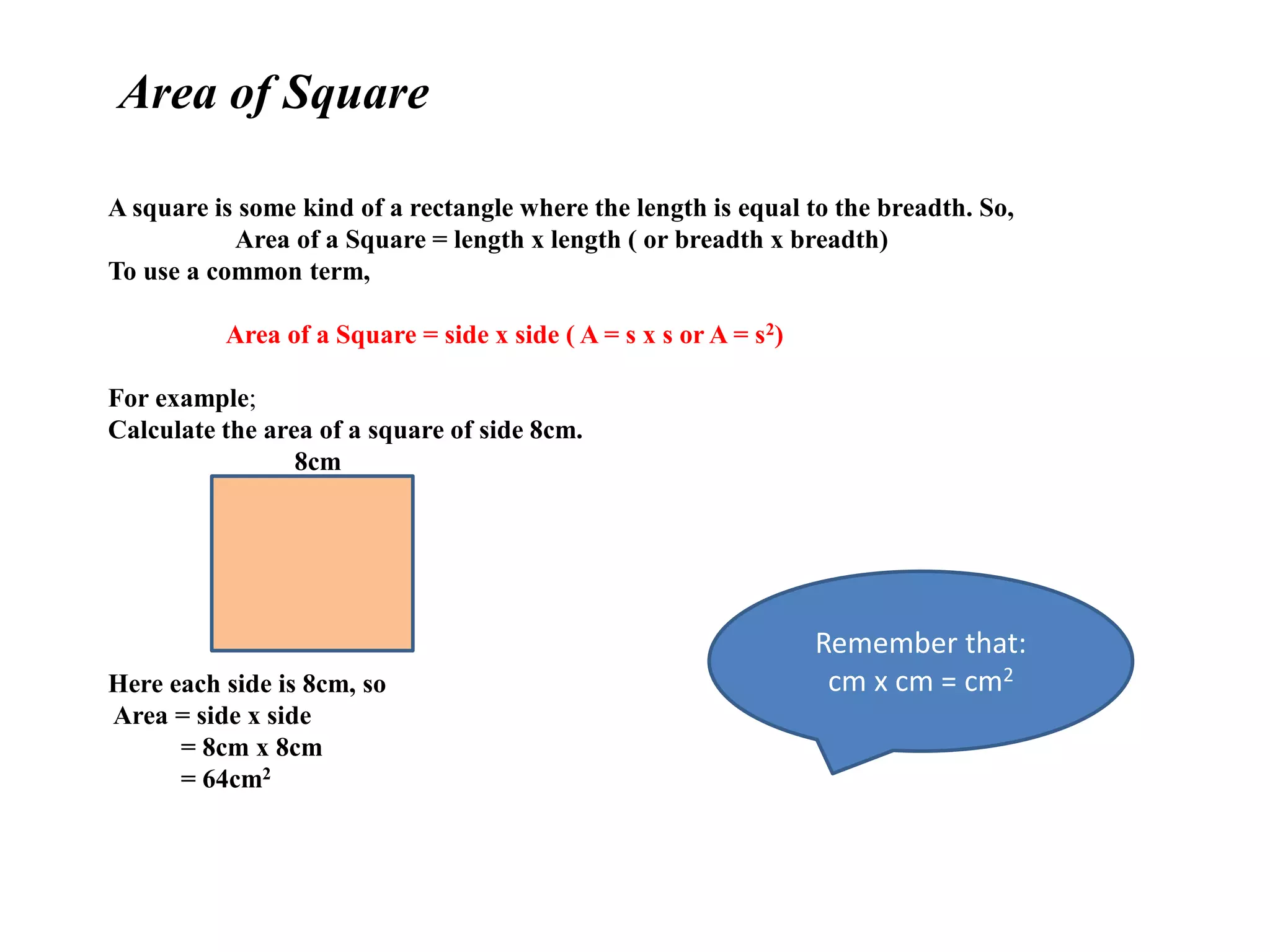
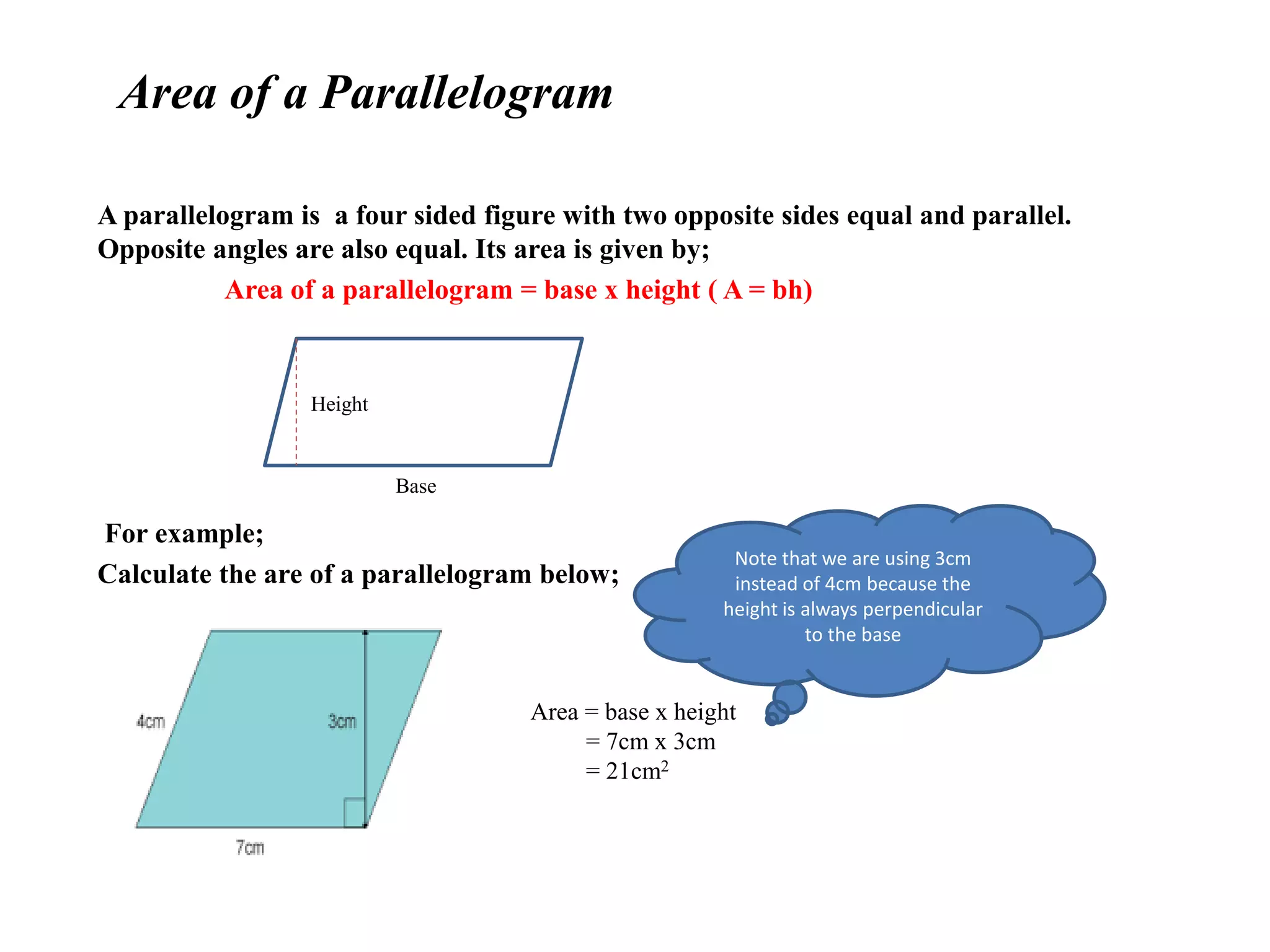
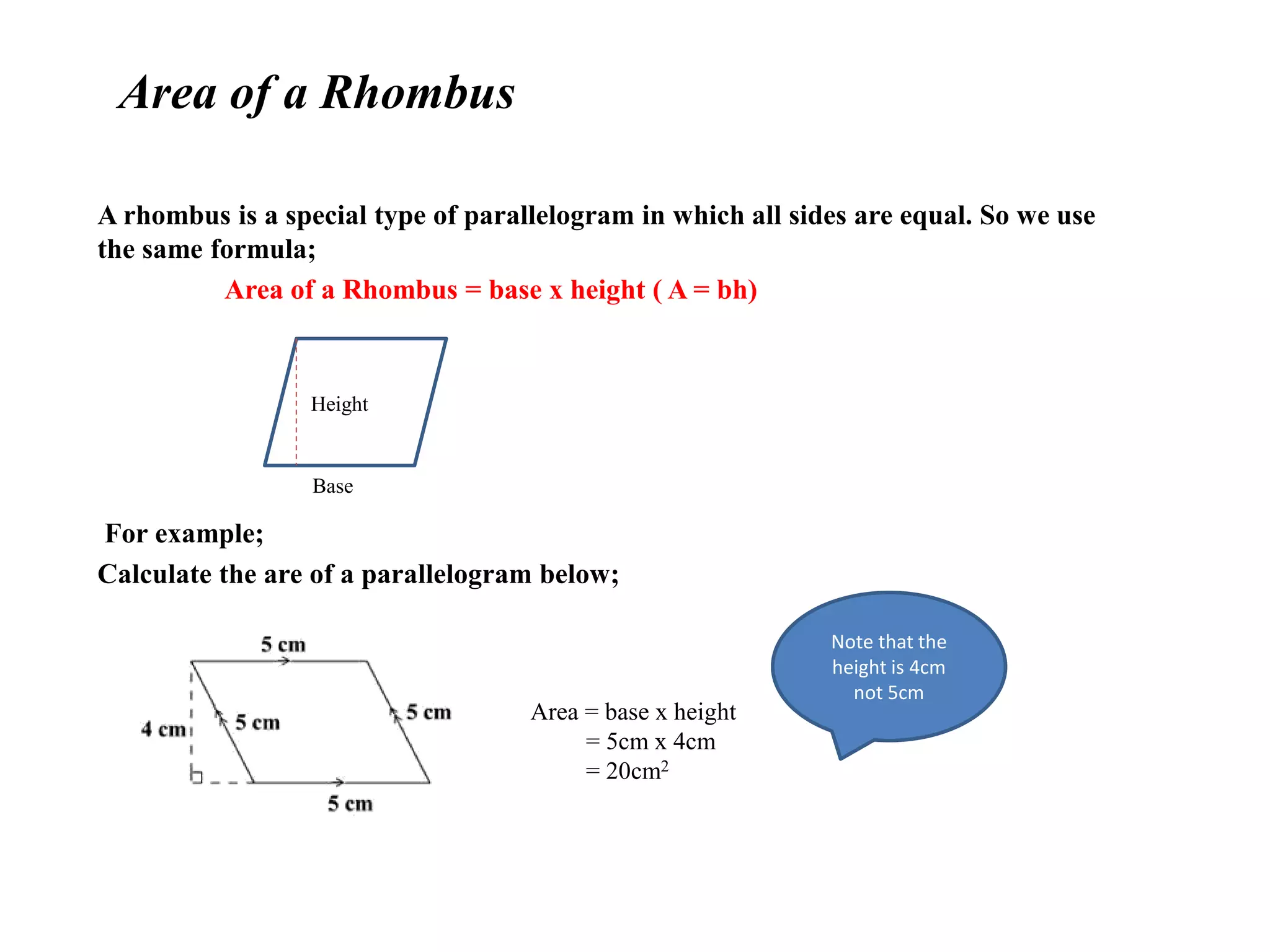
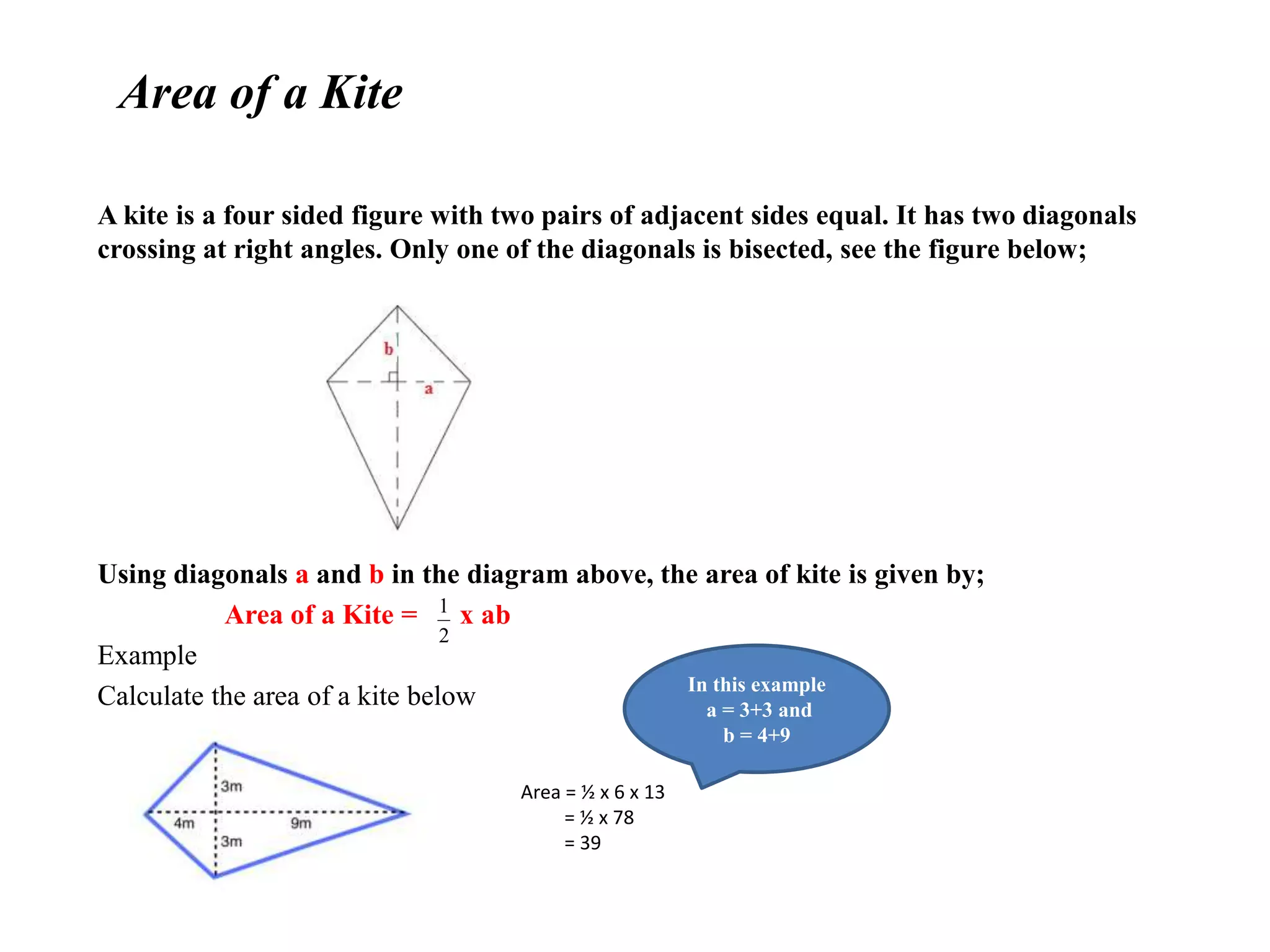
The document provides formulas for calculating the area of different shapes: - Rectangle: Area = length x width - Square: Area = side x side - Parallelogram: Area = base x height - Rhombus: Area = base x height - Kite: Area = 1/2 x diagonal 1 x diagonal 2 - Trapezium: Area = (sum of parallel sides) x height It includes examples of applying each formula to calculate the area of shapes with given dimensions measured in cm2.

1. Area of a rectangle
All the angles in a rectangle are 90o, so the area is given by:
Area of a rectangle = length x breadth ( A = lb)
For example;
12cm
7cm
Here the length is 12cm and the width is 7cm so,
Area = length x width
= 12cm x 7cm
= 84cm2
Remember that:
cm x cm = cm2

2. Area of Square
A square is some kind of a rectangle where the length is equal to the breadth. So,
Area of a Square = length x length ( or breadth x breadth)
To use a common term,
Area of a Square = side x side ( A = s x s or A = s2)
For example;
Calculate the area of a square of side 8cm.
8cm
Here each side is 8cm, so
Area = side x side
= 8cm x 8cm
= 64cm2
Remember that:
cm x cm = cm2

3. Area of a Parallelogram
A parallelogram is a four sided figure with two opposite sides equal and parallel.
Opposite angles are also equal. Its area is given by;
Area of a parallelogram = base x height ( A = bh)
For example;
Calculate the are of a parallelogram below;
Base
Height
Area = base x height
= 7cm x 3cm
= 21cm2
Note that we are using 3cm
instead of 4cm because the
height is always perpendicular
to the base

4. Area of a Rhombus
A rhombus is a special type of parallelogram in which all sides are equal. So we use
the same formula;
Area of a Rhombus = base x height ( A = bh)
For example;
Calculate the are of a parallelogram below;
Base
Height
Area = base x height
= 5cm x 4cm
= 20cm2
Note that the
height is 4cm
not 5cm

5. Area of a Kite
A kite is a four sided figure with two pairs of adjacent sides equal. It has two diagonals
crossing at right angles. Only one of the diagonals is bisected, see the figure below;
Using diagonals a and b in the diagram above, the area of kite is given by;
Area of a Kite = x ab
Example
Calculate the area of a kite below
2
1
Area = ½ x 6 x 13
= ½ x 78
= 39
In this example
a = 3+3 and
b = 4+9

6. Area of a Trapezium
A trapezium is another four sided figure with only one pair of opposite sides parallel to each other
as shown in the diagram below;
Using diagonals a, b and h in the diagram above, the area of kite is given by;
Area of a Trapezium = (a+b)h
Example
Calculate the area of a kite below
2
1
Area = ½ x (4+7)5
= ½ x 11 x 5
= 27.5