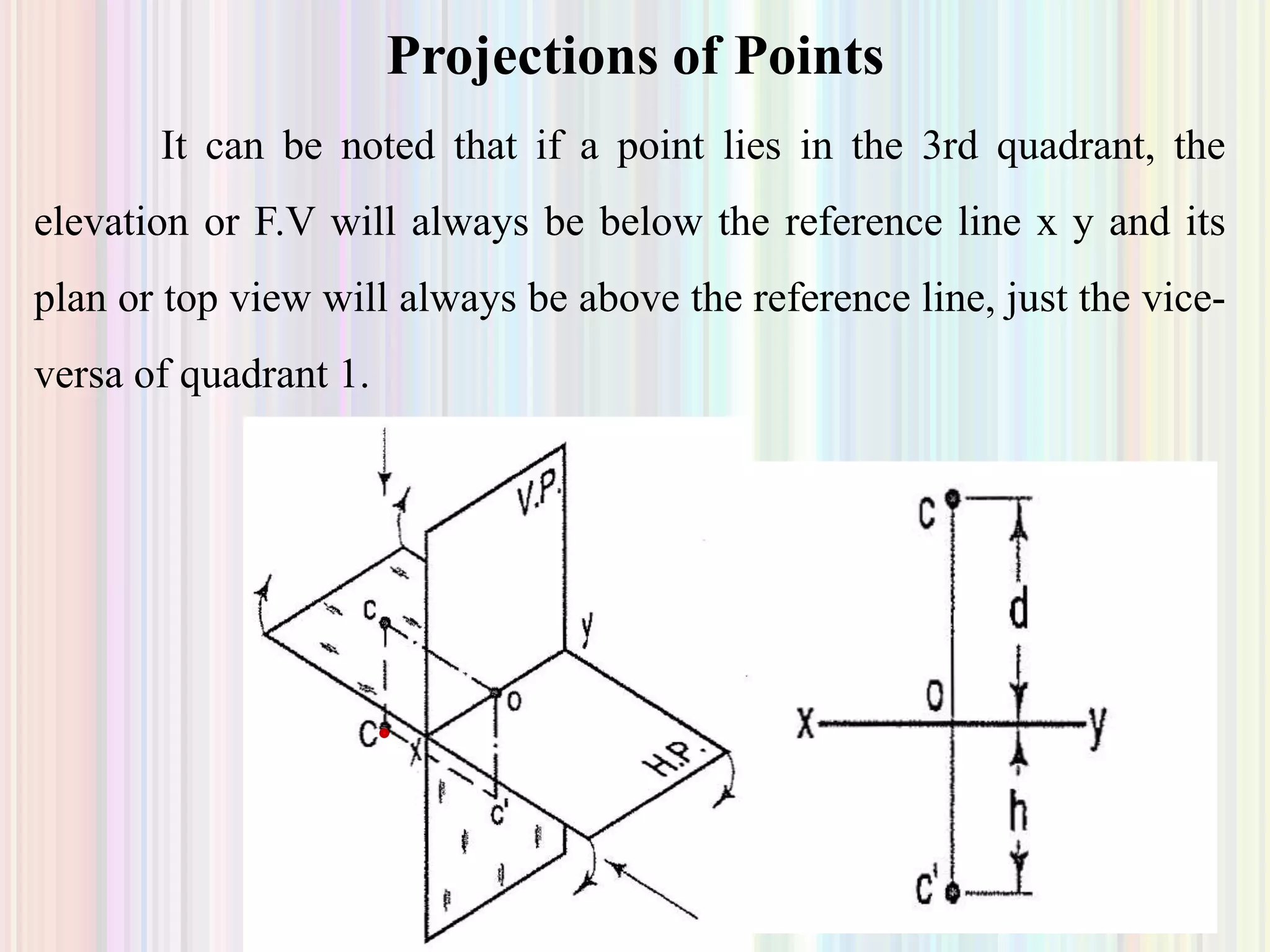
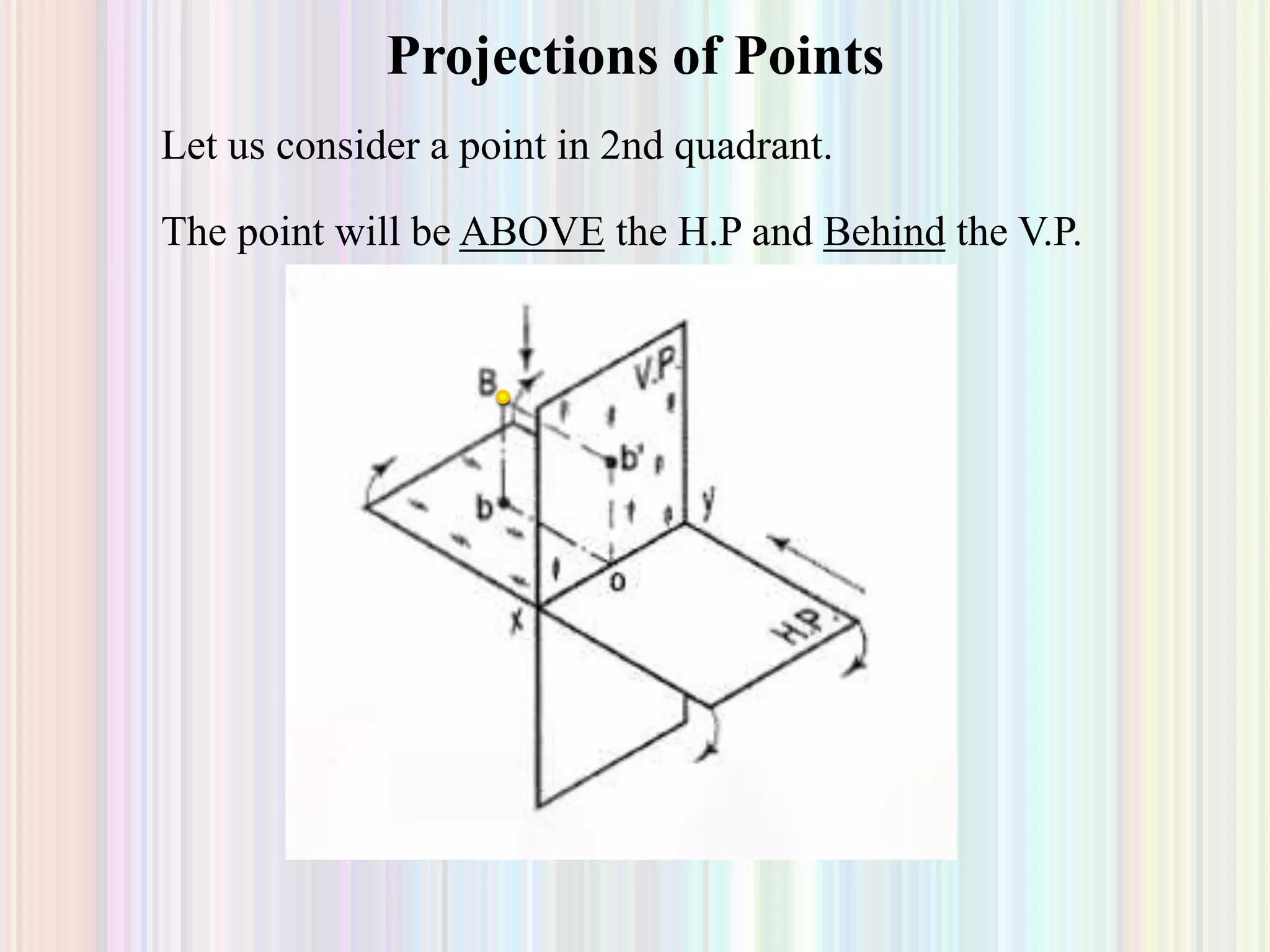
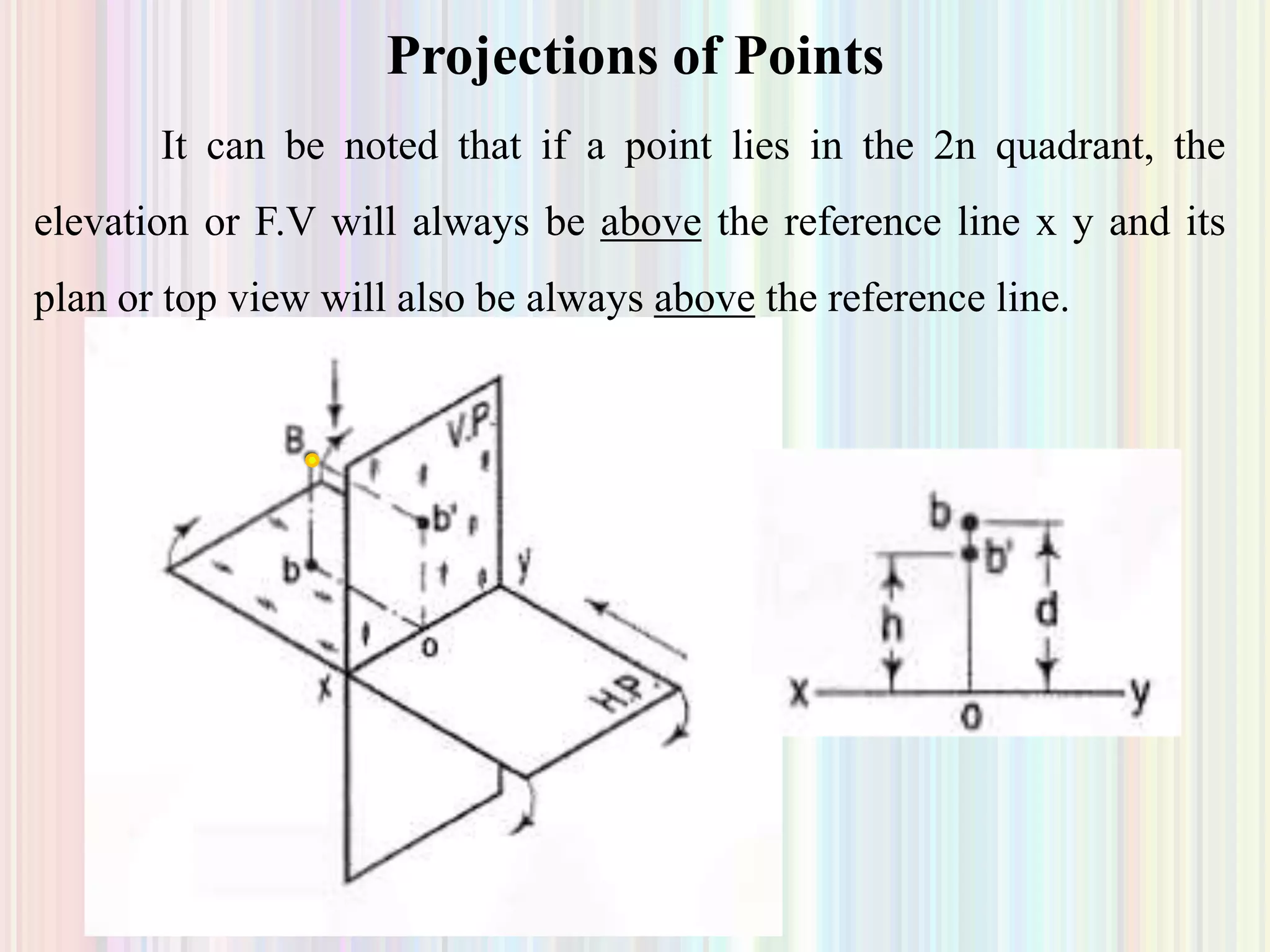
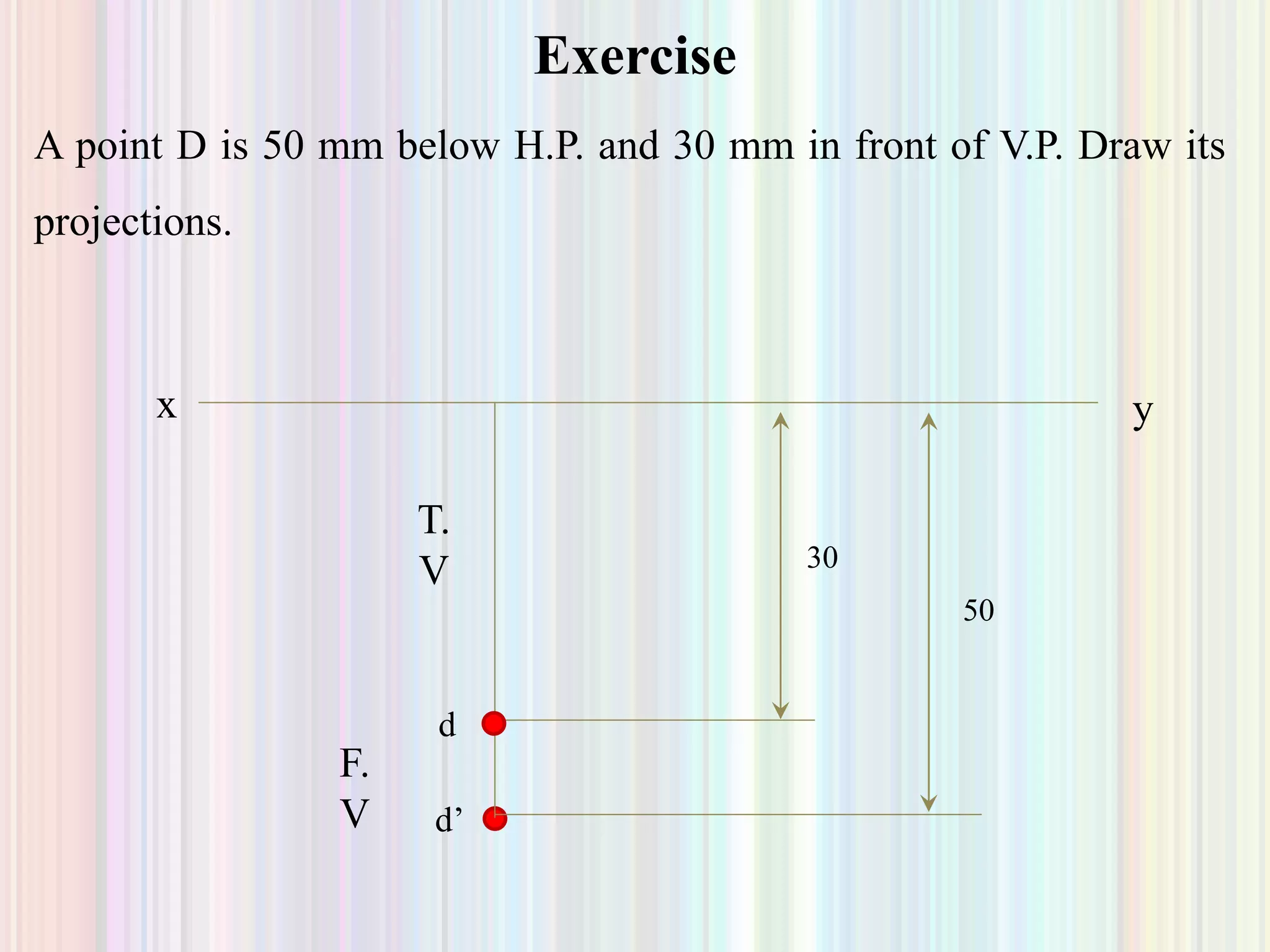
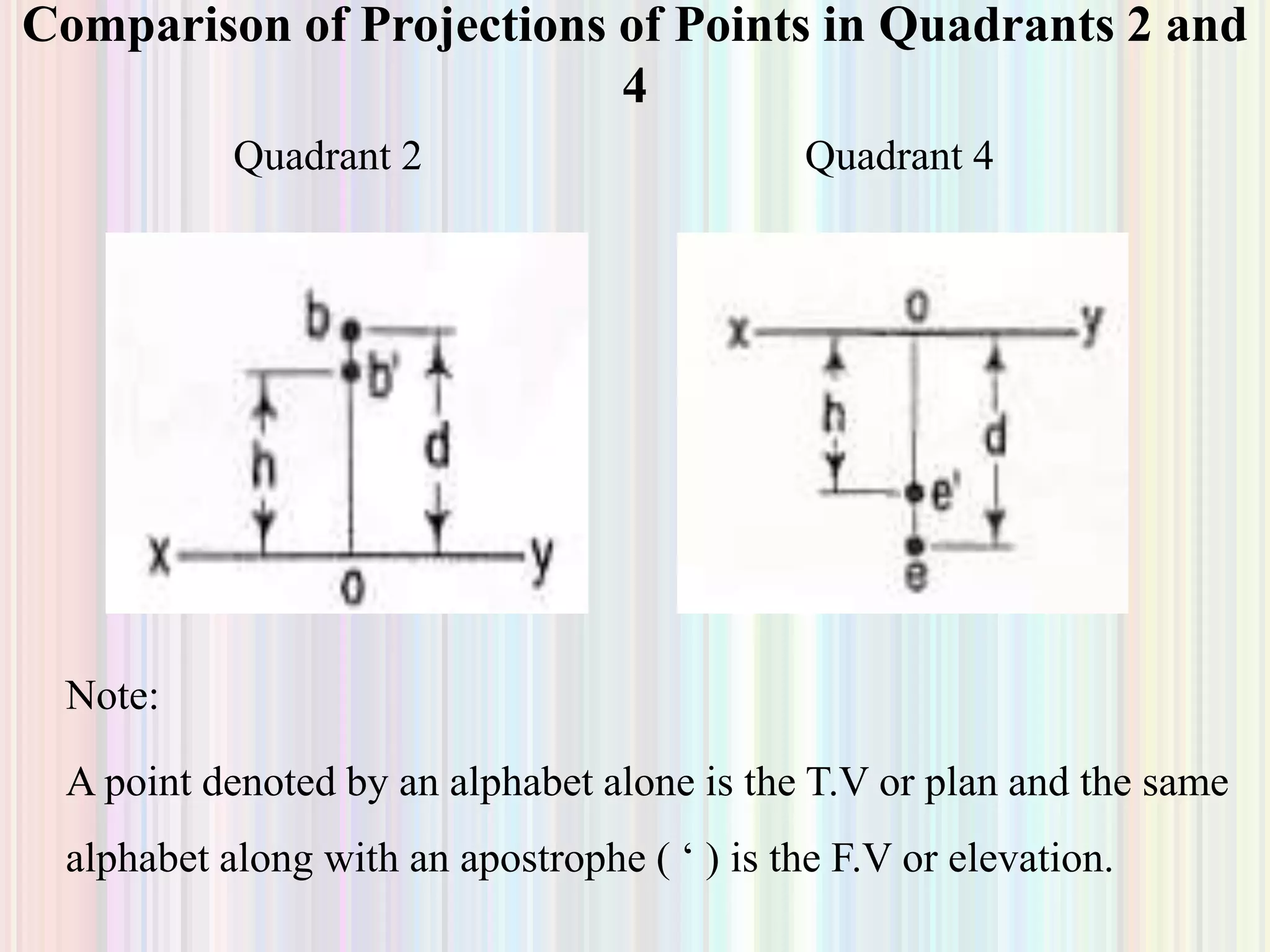
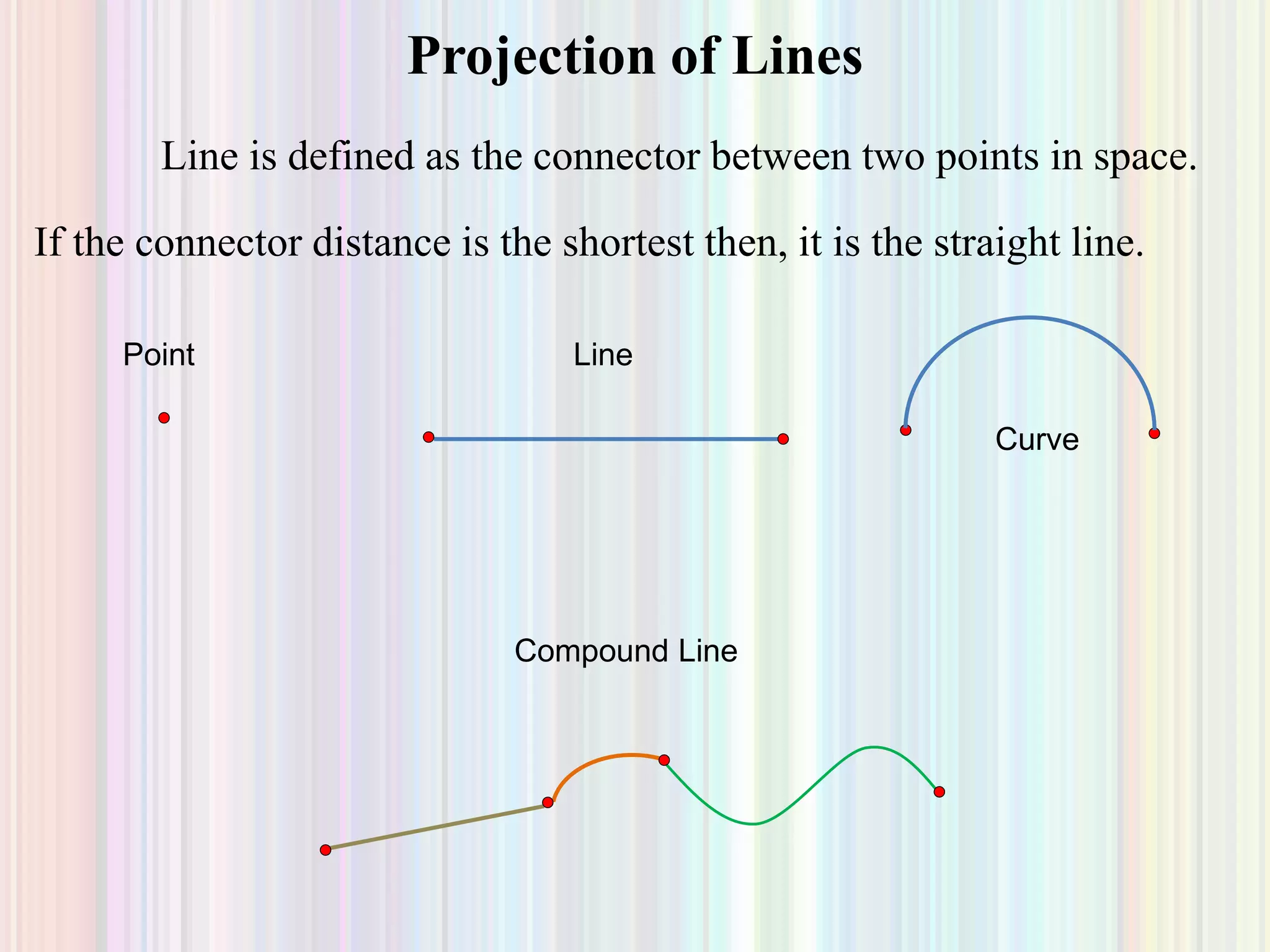
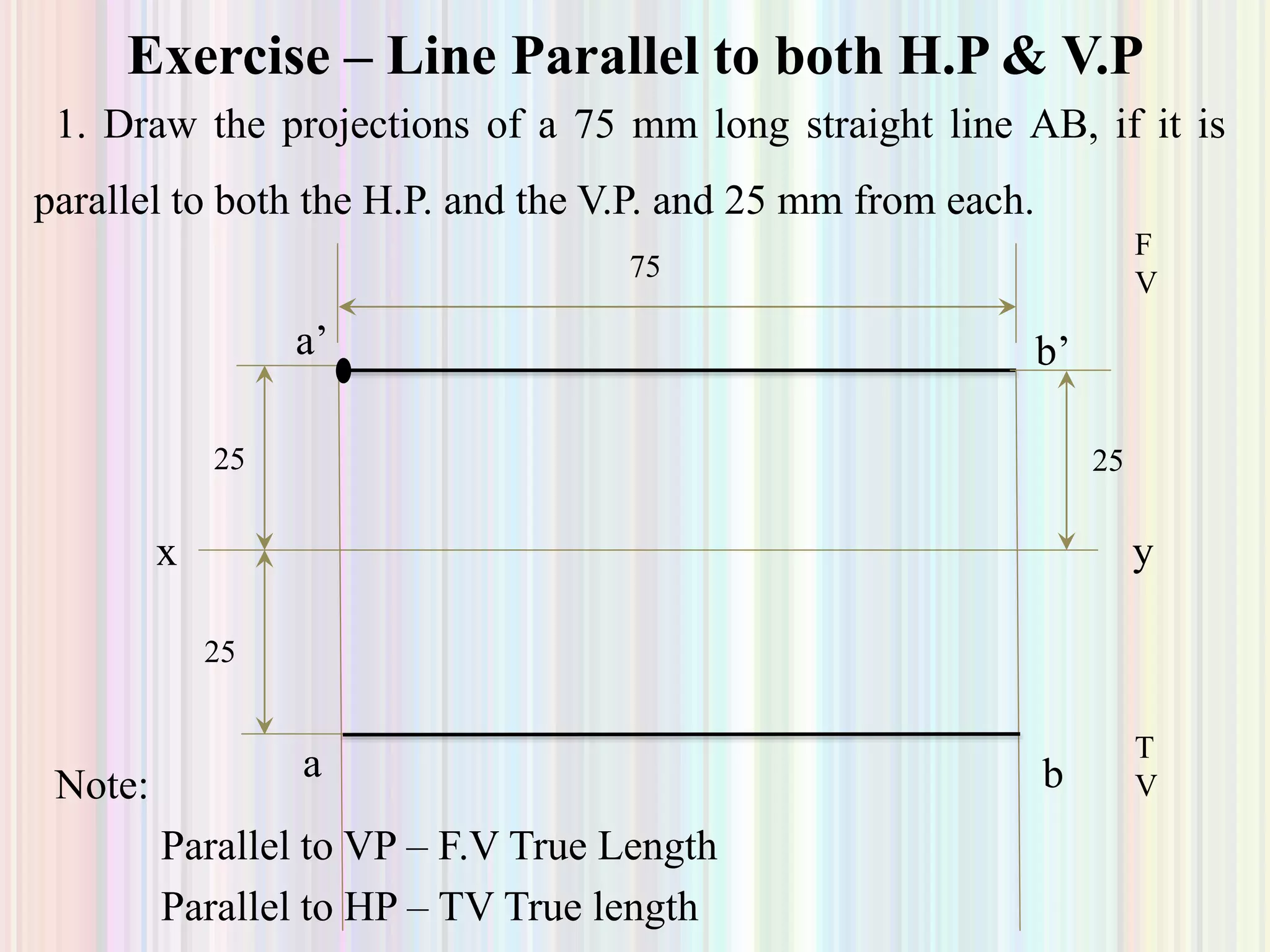
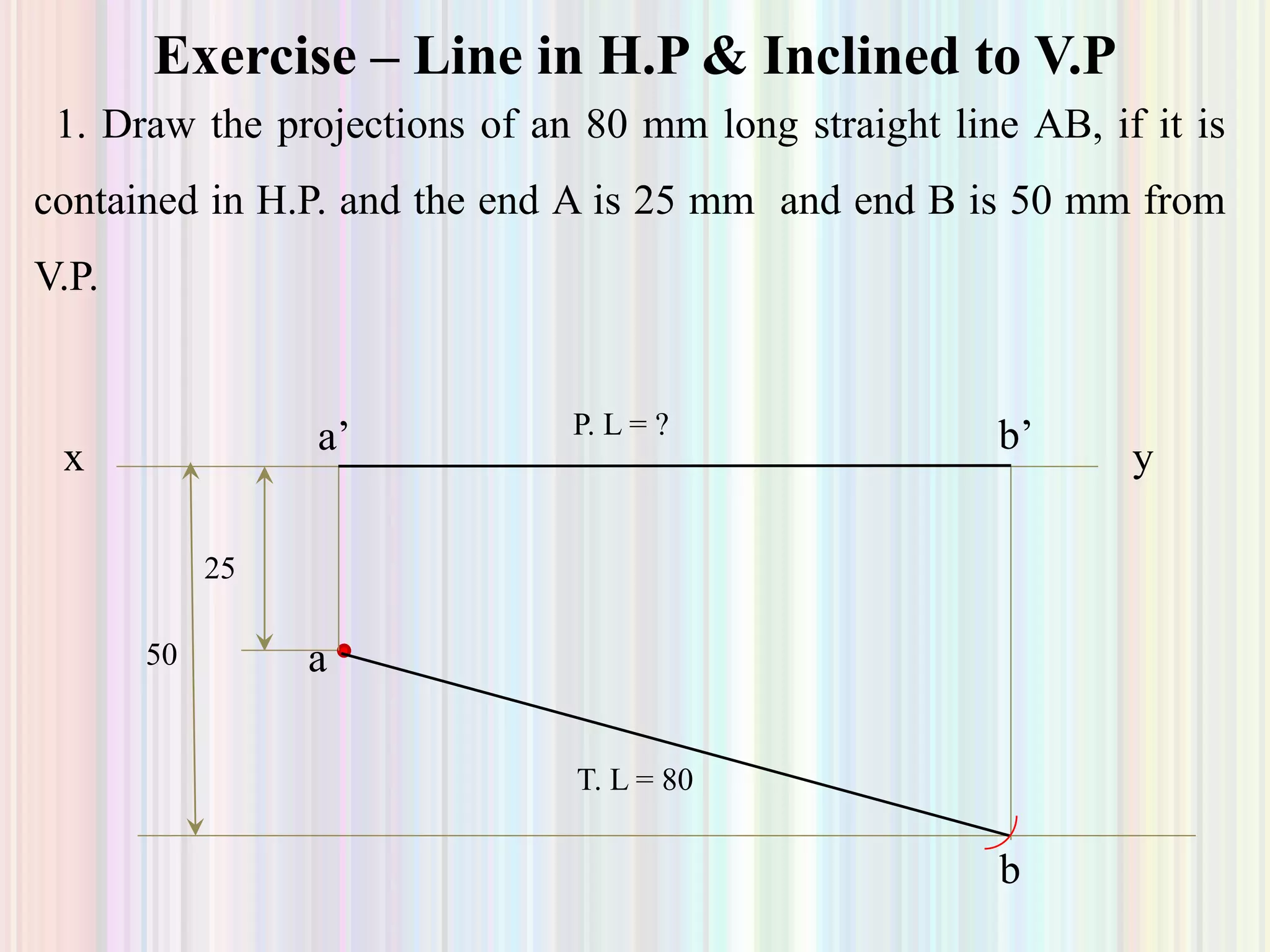
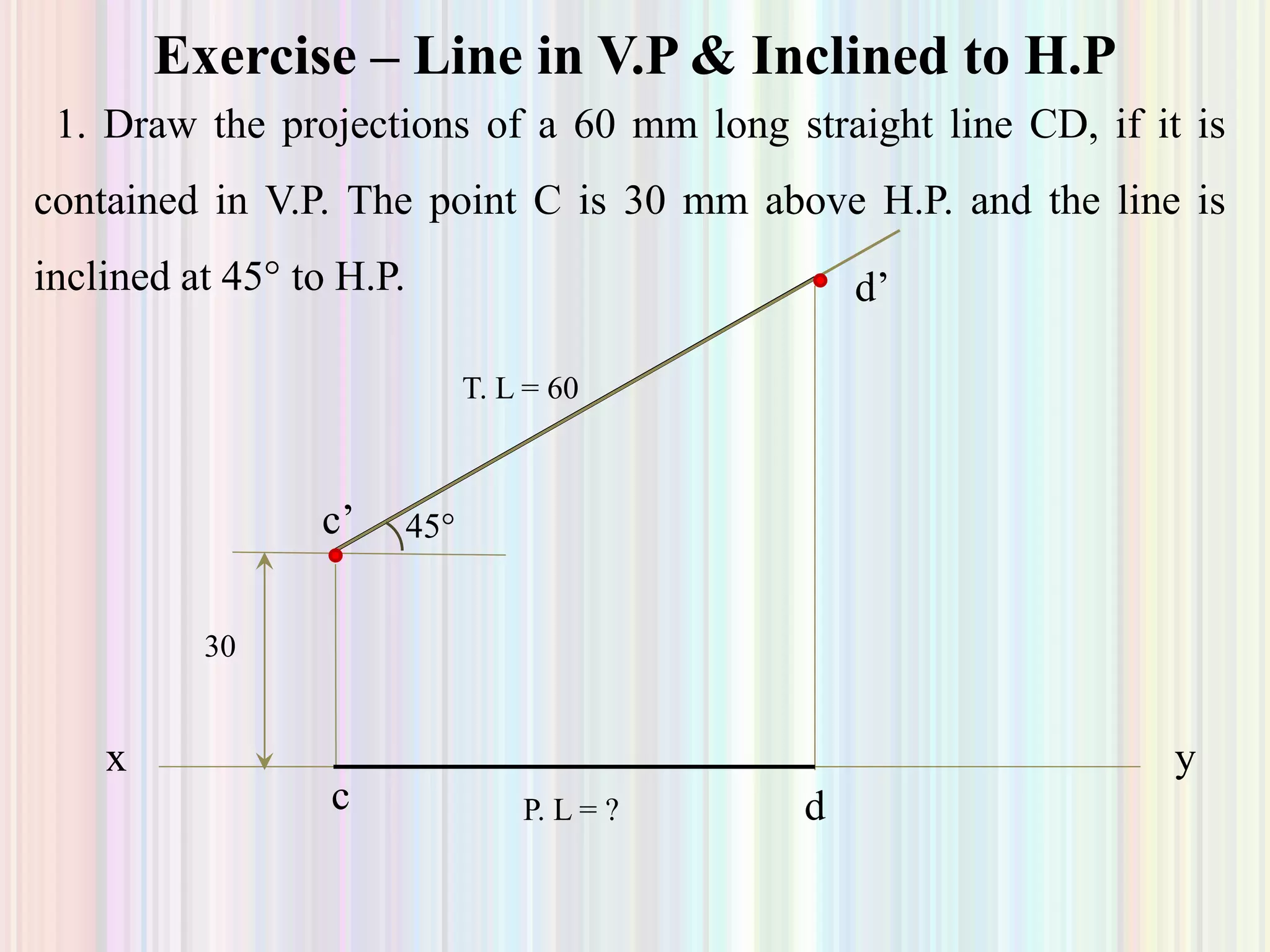
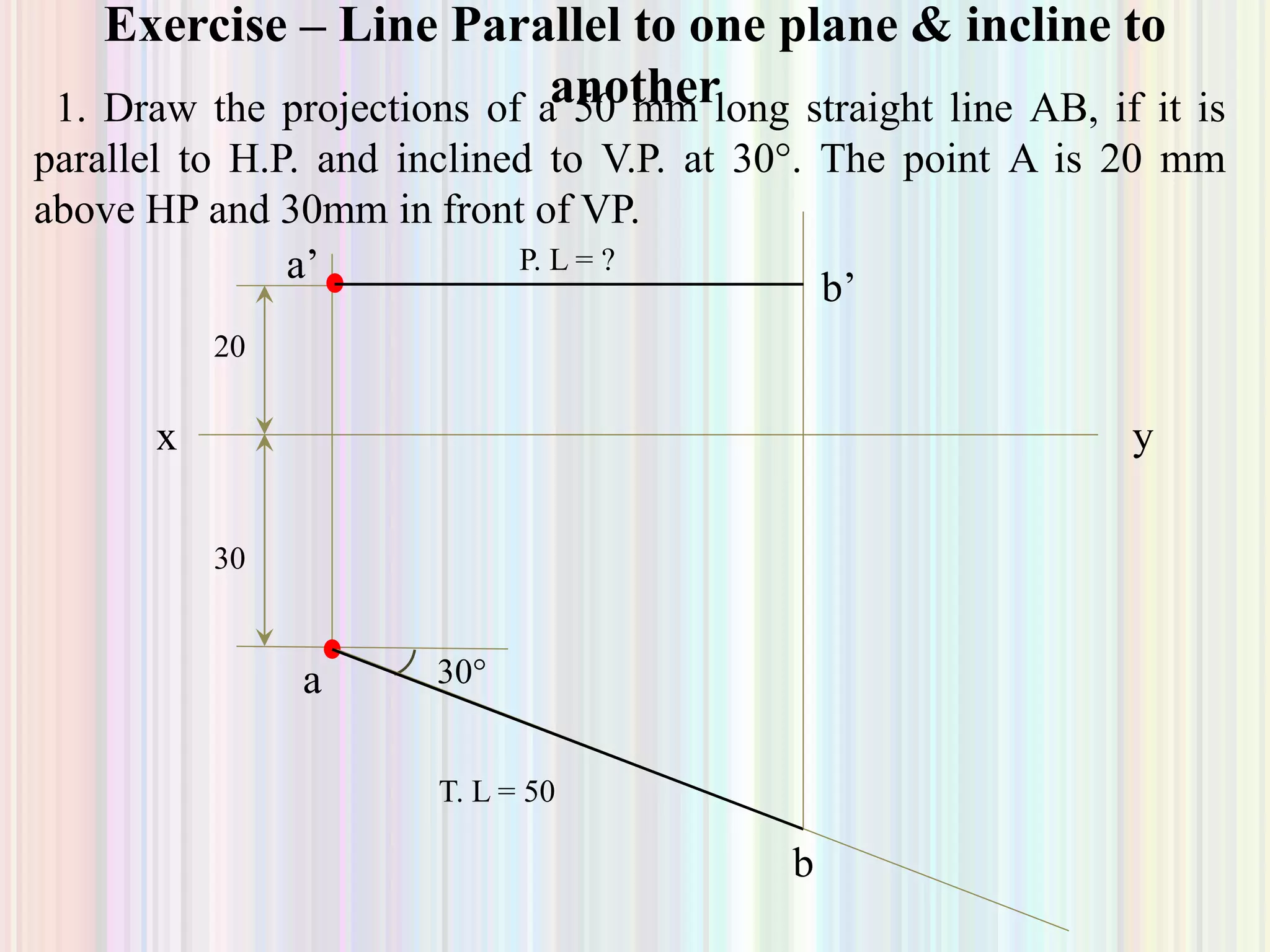
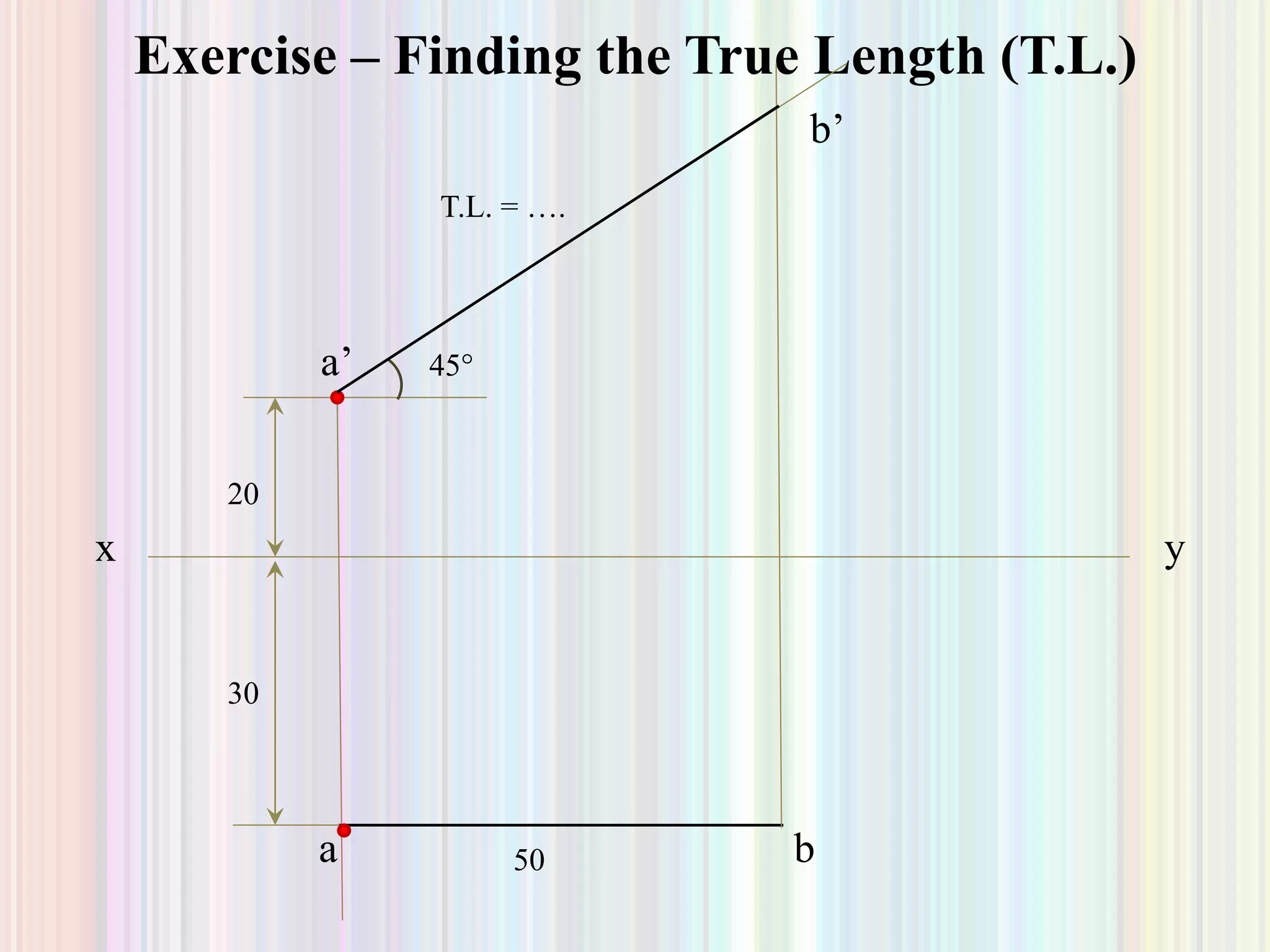
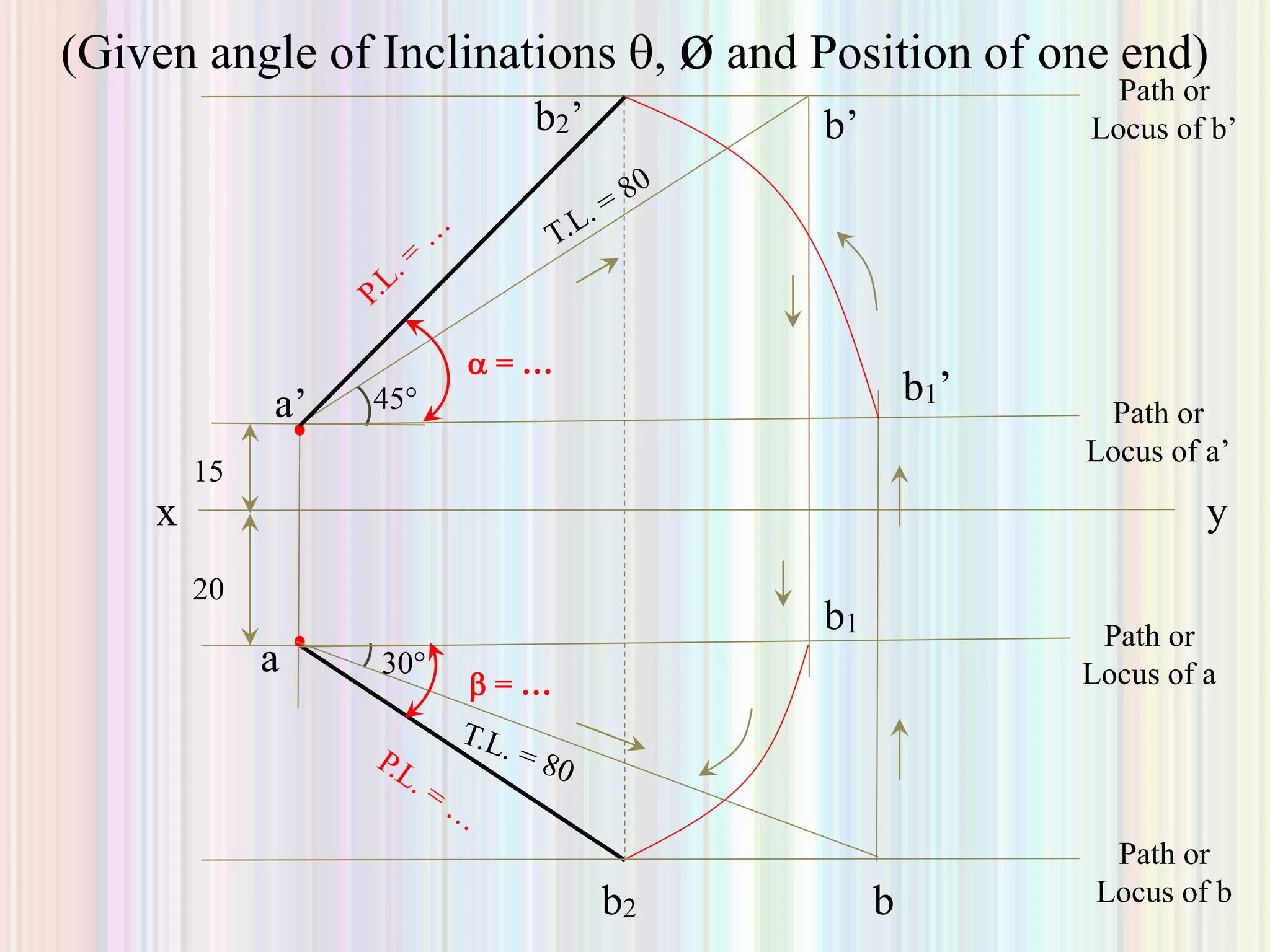
1. The document discusses the projection of points, lines, and plane surfaces. It provides examples of projecting points located in different quadrants and guidelines for indicating true lengths and projections of lines parallel or inclined to the planes. 2. Projection of lines is discussed for lines parallel to or contained within the planes, as well as lines inclined to one or both planes. Examples are given to demonstrate finding the true length, true inclination, or inclination angles of a line based on its projections. 3. Finding projections and true properties of a line is demonstrated through examples where the position of ends, inclination angles, or projected lengths are given to allow calculating the unknowns. Methods are outlined for drawing projections in different cases.

1. 20MEG01 Engineering Graphics
Module II
Prepared by:
M. Sundra Pandian, M.E., M.B.A.
Assistant Professor, Department of Mechanical Engineering,
Sri Ramakrishna Institute of Technology, Coimbatore - 10

2. Syllabus
Projection of Points, Lines and Plane Surfaces (Module 2)
Projection of points – Projection of straight lines (only First
angle projections) inclined to both the principal planes –
Determination of true lengths and true inclinations by rotating line
method and trapezoidal method and traces – Projection of planes
(polygonal and circular surfaces) inclined to both the principal planes
by rotating object method.

3. Introduction
A point may be situated, in space, in any one of the four
quadrants formed by the two principal planes of projection or may lie
in any one or both of them.

4. Introduction
Its projections are obtained by extending projectors
perpendicular to the planes.
x
y x y
V
P
H
P
Reference Line

5. Projection of Points
The projections in various quadrants are shown below.
Quadrant I
Above HP &
In front of VP
Quadrant II
Above HP &
Behind VP
Quadrant III
Below HP &
Behind VP
Quadrant IV
Below HP
In front of VP
V
P
H
P

6. Introduction
A point may be situated, in space, in any one of the four
quadrants formed by the two principal planes of projection or may lie
in any one or both of them.
Its projections are obtained by extending projectors
perpendicular to the planes.
One of the planes is then rotated so that the first and third
quadrants are opened out.
The projections are shown on a flat surface in their respective
positions either above or below or in xy

7. Projections of Points
Let the point “A” be on the first quadrant at a height of ‘h’
mm from the ground or Horizontal plane, H.P and at a distance of ‘y’
mm in front of the wall or vertical plane or V.P.
Lets draw the projections of the point A.
It is noted that the point is in
Quadrant 1.
Drawing the perpendicular
projector to the ground from the point
A, the projectors hits the H.P. at the
point a and similarly the V.P at a’.

8. Projections of Points
Let the point “A” be on the first quadrant at a height of ‘h’
mm ABOVE the ground or Horizontal plane, H.P and at a distance of
‘y’ mm IN FRONT OF the wall or vertical plane or V.P.
• The point will always be denoted in
lowercase letter.
• Elevation or Front view or F.V should
always be indicated with an apostrophe
( ‘ ).
• Plan or Top view or T.V should always
be indicated with the lowercase letter
without apostrophe ( ‘ ).

9. Projections of Points
It can be noted that if a point lies in the 1st quadrant, the
elevation or F.V will always be above the reference line x y and its
plan or top view will always be below the reference line.

10. Exercise
A point A is 50 mm above the ground and 60 mm in front of V.P.
Draw its projections.
x y
50
a’
60
a
F.
V
T.
V
Above HP – Above x y
Below HP – Below x y
In front of VP – Below x y
Behind VP – Above x y
HP dimension – F.V. – Have
‘
VP dimension – T.V. – No ‘

11. Projections of Points
Similarly let us consider a point in 3rd quadrant.
The point will be BELOW the H.P and Behind the V.P.

12. Projections of Points
It can be noted that if a point lies in the 3rd quadrant, the
elevation or F.V will always be below the reference line x y and its
plan or top view will always be above the reference line, just the vice-
versa of quadrant 1.

13. Exercise
A point C is 40 mm below the ground and 30 mm behind V.P. Draw
its projections.
x y
30
c
40
c’
T.
V
F.
V
HP dimension – F.V. – Have
‘
VP dimension – T.V. – No ‘

14. Comparison of Projections of Points in Quadrants 1 and
3
Quadrant 1 Quadrant 3
Note:
A point denoted by an alphabet alone is the T.V or plan and the same
alphabet along with an apostrophe ( ‘ ) is the F.V or elevation.

15. Projections of Points
Let us consider a point in 2nd quadrant.
The point will be ABOVE the H.P and Behind the V.P.

16. Projections of Points
It can be noted that if a point lies in the 2n quadrant, the
elevation or F.V will always be above the reference line x y and its
plan or top view will also be always above the reference line.

17. Exercise
A point B is 40 mm above the ground and 50 mm behind V.P. Draw
its projections.
x y
40
b’
50
b
F.
V
T.
V

18. Projections of Points
Let us consider a point in 4th quadrant.
The point will be BELOW the H.P and IN FRONT OF the V.P.

19. Projections of Points
It can be noted that if a point lies in the 2n quadrant, the
elevation or F.V will always be above the reference line x y and its
plan or top view will also be always above the reference line.

20. Exercise
A point D is 50 mm below H.P. and 30 mm in front of V.P. Draw its
projections.
x y
30
d’
50
d
F.
V
T.
V

21. Comparison of Projections of Points in Quadrants 2 and
4
Quadrant 2 Quadrant 4
Note:
A point denoted by an alphabet alone is the T.V or plan and the same
alphabet along with an apostrophe ( ‘ ) is the F.V or elevation.

22. q’
1. Draw the projections of the following points.
i. P is 40 mm above HP and 30mm in front of VP.
ii. Q is 30 mm above HP and 40 mm behind VP.
iii. R is 20 mm below HP and 35 mm behind VP.
iv. S is 30 mm below HP and 40 mm in front of VP
P’
Exercise
x y
40
30
P
30
40
q
20
r’
35
r
30
s’
40
s

23. 1. Draw the projections of the following points.
i. A is 50 mm above HP and 40mm behind VP.
ii. B is 35 mm below HP and 50 mm behind VP.
iii. C is 20 mm above HP and 35 mm in front of VP.
iv. D is 40 mm below HP and 50 mm in front of VP.
v. E is 35 mm in front of VP and on HP.
vi. F is on VP and 40 mm above HP.
vii. G is on both HP and VP.
viii. H is 35 mm below HP and on VP.
ix. I is 30 mm behind VP and on HP.
x. J is 40 mm in front of VP and on HP.
Exercise

24. Line is defined as the connector between two points in space.
If the connector distance is the shortest then, it is the straight line.
Projection of Lines
Point Line
Curve
Compound Line

25. Like the points is different quadrants, we will discuss about
the lines in different positions and its projections.
The projections will all be in the first quadrant or first angle
projections..
Projection of Lines

26. The line will either be parallel to Horizontal Plane (H.P) or
Vertical Plane (V.P.) to both planes (H.P & V.P)
The projections will all be in the first quadrant or first angle
projection as shown in the fig. below.
Line is Parallel to one or both planes

27. The actual or original or true length will always be shown in
the plane to which the line is parallel to.
The True length (T.L) will be the actual length of line which is
always shown only in the plane where the line is parallel.
So if the line is parallel to HP the top view or plan will show
the original length .
If the line is parallel to the VP, the true length will be shown or
can be measured from the front view or elevation.
If the line is parallel to both HP and VP, the true length is
shown in both the Front and Top views.
Line is Parallel to one or both planes

28. x
y
Reference Line
25
25
1. Draw the projections of a 75 mm long straight line, if it is parallel
to both the H.P. and the V.P. and 25 mm from each.
A
B
Exercise – Line Parallel to both H.P & V.P

29. 1. Draw the projections of a 75 mm long straight line AB, if it is
parallel to both the H.P. and the V.P. and 25 mm from each.
Exercise – Line Parallel to both H.P & V.P
x y
25
a’
75
b’
25
a b
25
Note:
Parallel to VP – F.V True Length
Parallel to HP – TV True length
F
V
T
V

30. x
y
The line will be lying in either H.P or V.P or both (in the
intersection of both planes i.e., at the reference line x-y).
A B
Exercise – Line contained in one or both planes.
C
D
E
F

31. x
y
Reference Line
Either the inclination angle will be given or the distance of
each end (e.g. A and B) of the line from the V.P will be given.
A
B
Exercise – Line contained in H.P & Inclined to V.P
ø°
a’
b’

32. 1. Draw the projections of an 80 mm long straight line AB, if it is
contained in H.P. and the end A is 25 mm and end B is 50 mm from
V.P.
Exercise – Line in H.P & Inclined to V.P
x y
25
a
b
a’ b’
T. L = 80
P. L = ?
50

33. 30°
1. Draw the projections of a 80 mm long straight line AB, if it is
contained in H.P. The point A is 25 mm in front of V.P. and the line is
inclined at 30° to V.P.
Exercise – Line in H.P & Inclined to V.P
x y
25
a
T. L = 80
b
a’ b’
P. L = ?

34. x
y
Reference Line
Either the inclination angle will be given or the distance of
each end (e.g. A and B) of the line from the V.P will be given.
A
B
Exercise – Line contained in V.P & Inclined to H.P
°

35. d’
1. Draw the projections of a 70 mm long straight line CD, if it is
contained in V.P. and the end C is 30 mm and end D is 60 mm above
H.P.
Exercise – Line in V.P & Inclined to H.P
x y
30
c’
60
c d
T. L = 70
P. L = ?

36. 1. Draw the projections of a 60 mm long straight line CD, if it is
contained in V.P. The point C is 30 mm above H.P. and the line is
inclined at 45° to H.P.
45°
Exercise – Line in V.P & Inclined to H.P
x y
30
c
T. L = 60
d
c’
d’
P. L = ?

37. x
y
d
Either the inclination angle will be given or the distance of
each end (e.g. A and B) of the line from the V.P will be given.
E
F
Exercise – Line Parallel to H.P & Perpendicular to
V.P
ø°

38. 1. Draw the projections of a 50 mm long straight line AB, if it is
parallel to H.P. and inclined to V.P. at 30°. The point A is 20 mm
above HP and 30mm in front of VP.
Exercise – Line Parallel to one plane & incline to
another
x y
30
a 30°
T. L = 50
b
20
a’
b’
P. L = ?

39. x
y
Reference Line
25
25
The projection will be true length will be shown in the plane
where the line is parallel.
The projection of the line will be a point in the plane where it
is perpendicular.
A
B
Line Parallel to one plane & Perpendicular to
another
x
y
25
25
A
B

40. Line Parallel to one plane & Perpendicular to
another
Case 1:-
The line is parallel to HP
and perpendicular to VP.
x y
a
b
Case 2:-
The line is parallel to VP
and perpendicular to HP.
x y
a’
b’
(a’) b’
(a ) b

41. E.g: The top view of a line, parallel to V.P and inclined 45 ° to the
H.P is 50 mm. One end of the line is 20 mm above H.P and 30 mm
in front of V.P. Draw the projections and find the true length of
the line.
In these kind of problems, the location of the points, angle of
inclination and the projected length will be given and the true
length of the line will be required.
So the projected length is drawn and the true or original length
of the line will be derived from it in the reverse drawing method
as followed in the previous problems.
Exercise – To find the True Length (T.L)

42. 45°
a
a’
Exercise – Finding the True Length (T.L.)
x y
20
30
b
b’
50
T.L. = ….

43. a
1. The front view of a 75 mm long line measures 55 mm. The line
is parallel to H.P and one end is in V.P. and 25 mm above H.P.
Draw the projections of the line and its inclination to V.P.
Exercise – To find True Inclination
x y
25
a’ 55 b’
R = T.L. = 75
b
Ø = …

44. Line Inclined to both planes
In this case the line will be inclined to H.P at an angle of
‘’ and inclined to V.P at an angle of ‘ø’.
So the true length can be readily available in any plane to
project to the other plane.
A
B
ø °
° H.P
Inclination
V.P
Inclination

45. 1. Draw the projections of aN 80 mm long straight line GH, if it is
inclined at 45° to H.P. and 30° to V.P. The point G is 15 mm above HP
and 20 mm in front of V.P.
Hint: H.P Dimension & angle – Above x-y
V.P Dimension & angle – Below x-y
Whenever a line is inclined to a plane, the true
length can’t be measured from the projections.
Exercise – Line Inclined to Both Planes

46. (Given angle of Inclinations , ø and Position of one end)
x y
15
a’
1. Draw the projections of a 80 mm long straight line, if it is inclined
at 45° to H.P. and 30° to V.P. One end is 15 mm above HP and 20 mm
in front of V.P.
Method:
• First assume the line is inclined to H.P. and parallel to V.P.
Draw the front view. Then assume the line is inclined to
V.P. and parallel to H.P.
• Then the original length of the line will be projected in the
front view.
45°
b’

47. 45°
(Given angle of Inclinations , ø and Position of one end)
x y
15
a’
b’
20
Path or
Locus of a’
Path or
Locus of b’
a 30°
b
Path or
Locus of a
Path or
Locus of b
b1
b1’
b2’
 = …
b2
 = …

48. (Given Positions of both ends
To find the angle of inclinations )
1. Draw the projections of a 70 mm long straight line, having its left
end 20 mm above H.P. and 25 mm in front of V.P. and the right end is
40 mm above the H.P. and 50 mm in front of V.P. Draw the
projections and find the inclinations of the line.
Method:
• First assume the line is inclined to H.P. and parallel to V.P.
Draw the front view. Then assume the line is inclined to
V.P. and parallel to H.P.
• Then the original or true inclinations of the line will be
determined in the reverse method as used in the previous
problem.
• When the lines are extended they meet the H.P and or the
V.P. This extended meeting point is called the trace

49. b2
(Given Position of both ends
To find angle of Inclinations  and ø)
x y
20
a’
Path of a’
25
Path of a
a
40
Path of b’
R = T.L. = 70
b’
50
Path of b
b
b1
b1’’
R = T.L. = 70
b2’’
° = …
° = …
ø° = …
° = …

50. Syllabus
Projection of Points, Lines and Plane Surfaces (Module 2)
Projection of points – Projection of straight lines (only First
angle projections) inclined to both the principal planes –
Determination of true lengths and true inclinations by rotating line
method and trapezoidal method and traces – Projection of planes
(polygonal and circular surfaces) inclined to both the principal planes
by rotating object method.