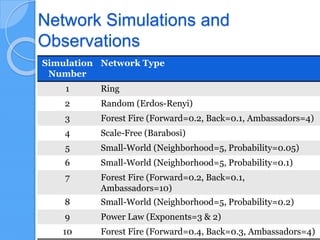
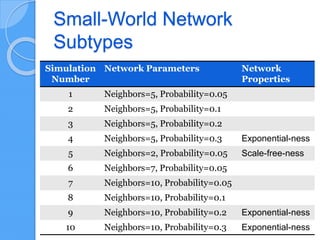
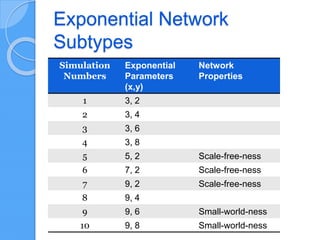
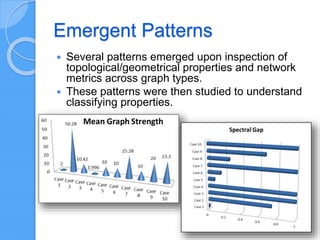
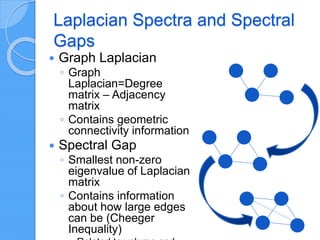
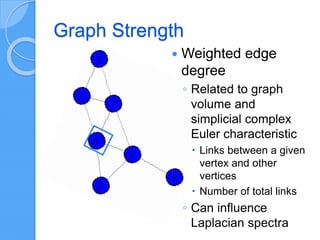
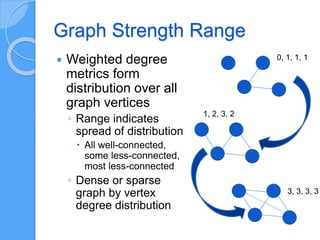
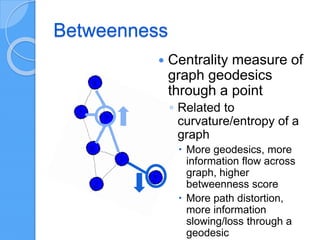
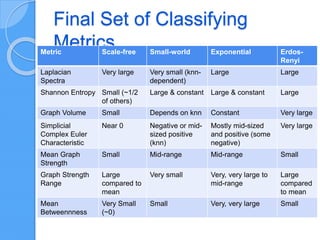
The document discusses empirical network classification based on various network metrics and behaviors observed through simulations of different network types. It highlights patterns in topological properties and introduces metrics such as graph strength, Laplacian spectra, and Shannon entropy to classify networks effectively. Conclusions indicate that a small set of efficient topological metrics can reliably distinguish between different types of generated networks.

1. Empirical Network
Classification through Network
Metrics
Colleen M. Farrelly

2. BACKGROUND AND
SIMULATIONS

3. Problem Overview
 Graphs/networks have
different structure,
dependent on link
distributions.
 Graph algorithms can give
varying performance
dependent on the network
structure.
 Classifying networks can
help with algorithm design
and predictive analytics
problem-shooting.

4. Network Simulations and
Observations
Simulation
Number
Network Type
1 Ring
2 Random (Erdos-Renyi)
3 Forest Fire (Forward=0.2, Back=0.1, Ambassadors=4)
4 Scale-Free (Barabosi)
5 Small-World (Neighborhood=5, Probability=0.05)
6 Small-World (Neighborhood=5, Probability=0.1)
7 Forest Fire (Forward=0.2, Back=0.1,
Ambassadors=10)
8 Small-World (Neighborhood=5, Probability=0.2)
9 Power Law (Exponents=3 & 2)
10 Forest Fire (Forward=0.4, Back=0.3, Ambassadors=4)

5. Small-World Network
Subtypes
Simulation
Number
Network Parameters Network
Properties
1 Neighbors=5, Probability=0.05
2 Neighbors=5, Probability=0.1
3 Neighbors=5, Probability=0.2
4 Neighbors=5, Probability=0.3 Exponential-ness
5 Neighbors=2, Probability=0.05 Scale-free-ness
6 Neighbors=7, Probability=0.05
7 Neighbors=10, Probability=0.05
8 Neighbors=10, Probability=0.1
9 Neighbors=10, Probability=0.2 Exponential-ness
10 Neighbors=10, Probability=0.3 Exponential-ness

6. Exponential Network
Subtypes
Simulation
Numbers
Exponential
Parameters
(x,y)
Network
Properties
1 3, 2
2 3, 4
3 3, 6
4 3, 8
5 5, 2 Scale-free-ness
6 7, 2 Scale-free-ness
7 9, 2 Scale-free-ness
8 9, 4
9 9, 6 Small-world-ness
10 9, 8 Small-world-ness

7. RESULTS EXEGESIS

8. Emergent Patterns
 Several patterns emerged upon inspection of
topological/geometrical properties and network
metrics across graph types.
 These patterns were then studied to understand
classifying properties.

9. Laplacian Spectra and Spectral
Gaps
 Graph Laplacian
◦ Graph
Laplacian=Degree
matrix – Adjacency
matrix
◦ Contains geometric
connectivity information
 Spectral Gap
◦ Smallest non-zero
eigenvalue of Laplacian
matrix
◦ Contains information
about how large edges
can be (Cheeger
Inequality)

10. Shannon Entropy
 Related to network
entropy (flow of
information across
graph)
◦ Measure of pair-wise
vertex information
exchange
 Connection to network
diffusion and Markov
chain convergence
 Technically, amount of
distortion on graph
◦ Crude measure of
network Ricci
curvature

11. Graph Volume
 Related to
curvature
◦ Curvature
defines
deviation of
volume from
that of a
standard
shape.
 Area of
stretched circle
greater than

12. Simplicial Complex Euler
Characteristic
 Euler characteristic as
topological invariant
◦ Hole-counting in object by
dimensionality of hole
◦ Simplicial complex version
gives more distinguishing
metric than graph version
 Linked to curvature and
other geometric properties
through Gauss-Bonnet
Theorem:
◦ 𝐾 𝜕𝐴 + K 𝜕 𝑠 =2πΧ(M)

13. Graph Strength
 Weighted edge
degree
◦ Related to graph
volume and
simplicial complex
Euler characteristic
 Links between a given
vertex and other
vertices
 Number of total links
◦ Can influence
Laplacian spectra

14. Graph Strength Range
 Weighted degree
metrics form
distribution over all
graph vertices
◦ Range indicates
spread of distribution
 All well-connected,
some less-connected,
most less-connected
◦ Dense or sparse
graph by vertex
degree distribution
0, 1, 1, 1
1, 2, 3, 2
3, 3, 3, 3

15. Betweenness
 Centrality measure of
graph geodesics
through a point
◦ Related to
curvature/entropy of a
graph
 More geodesics, more
information flow across
graph, higher
betweenness score
 More path distortion,
more information
slowing/loss through a
geodesic

16. CLASSIFYING METRICS
AND NETWORK
ASYMPTOTICS

17. Practical Classification
 Measure empirical graph’s metric
properties.
 Simulate networks with a similar
number of vertices and known
underlying degree distribution.
 Measure random networks’ metric
properties.
 Compare empirical graph to random
graphs to classify graph with best-
fitting measurements.

18. Final Set of Classifying
MetricsMetric Scale-free Small-world Exponential Erdos-
Renyi
Laplacian
Spectra
Very large Very small (knn-
dependent)
Large Large
Shannon Entropy Small (~1/2
of others)
Large & constant Large & constant Large
Graph Volume Small Depends on knn Constant Very large
Simplicial
Complex Euler
Characteristic
Near 0 Negative or mid-
sized positive
(knn)
Mostly mid-sized
and positive (some
negative)
Very large
Mean Graph
Strength
Small Mid-range Mid-range Small
Graph Strength
Range
Large
compared to
mean
Very small Very, very large to
mid-range
Large
compared
to mean
Mean
Betweennness
Very Small
(~0)
Small Very, very large Small

19. Asymptotics of Graph Types
Very small KNN
value with lower
link probabilities
Large KNN value
with high link
probabilities
Large
second
parameter
Small
second
parameter
Scale-free
Small-worldExponential

20. CONCLUSIONS

21. Conclusions
 A small set of computationally-efficient
topological metrics can distinguish
among graphs generated by different
network types.
 Using these metrics, it is possible to
classify an unknown network as one of
these network types based on its
measured topological metrics.