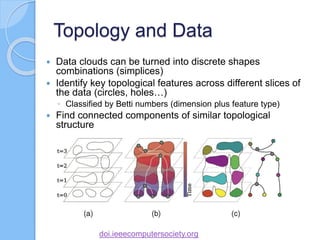
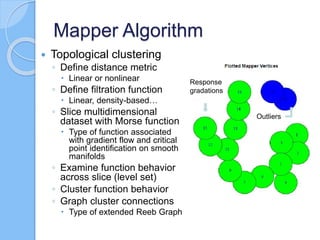
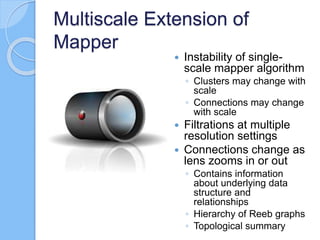
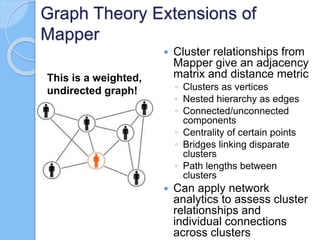
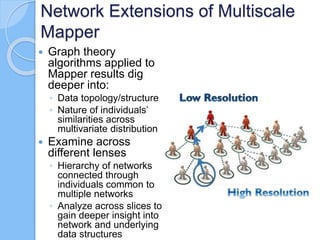
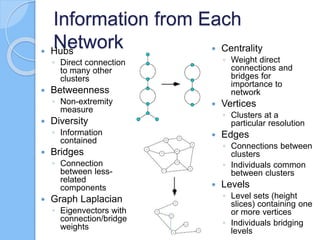
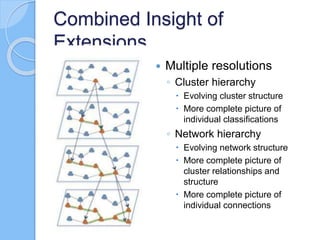
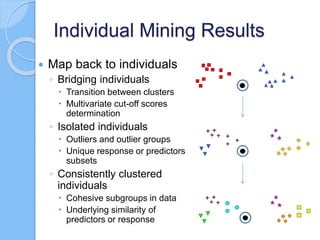
The document discusses multiscale mapper networks as a solution to limitations of current clustering methods, emphasizing the need to capture underlying structures and relationships in high-dimensional data. It introduces key concepts like topological clustering, the mapper algorithm, and network analytics for assessing cluster relationships. The proposed method aims to improve robustness, stability, and hierarchical representations of data while effectively handling complex structures.

1. Multiscale Mapper Networks
By Colleen M. Farrelly

2. Problem
 Data contains many
underlying structures
and relationships.
 Current methods (such
as k-means
clustering):
◦ Don’t capture all of these
structures
◦ Struggle with certain
data properties
(dimensionality)
◦ Provide little information
about connectedness
between
clusters/individuals
◦ Instability

3. Recent Solutions
 Nonlinear distance
metrics
◦ Random forest-based
◦ Manifold learning-based
 Hierarchical clustering
◦ Nested clustering
approach
 Multiscale K-Nearest
Neighbors
◦ Adjust number of
neighbors to slice data
 Still don’t provide a
comprehensive view of
data structure

4. Topology Overview
 Branch of mainly pure
mathematics
 Study of changes in
function behavior on
different shapes
(called manifolds)
 Can examine locally-
variant and globally-
invariant properties
 Classify
similarities/differences
between shapes
based on these
characteristics
Algebra can be used to build
more complex structures
from basic building blocks

5. Topology and Data
 Data clouds can be turned into discrete shapes
combinations (simplices)
 Identify key topological features across different slices of
the data (circles, holes…)
◦ Classified by Betti numbers (dimension plus feature type)
 Find connected components of similar topological
structure
doi.ieeecomputersociety.org

6. Mapper Algorithm
 Topological clustering
◦ Define distance metric
 Linear or nonlinear
◦ Define filtration function
 Linear, density-based…
◦ Slice multidimensional
dataset with Morse function
 Type of function associated
with gradient flow and critical
point identification on smooth
manifolds
◦ Examine function behavior
across slice (level set)
◦ Cluster function behavior
◦ Graph cluster connections
 Type of extended Reeb Graph
Response
gradations
Outliers

7. Multiscale Extension of
Mapper
 Instability of single-
scale mapper algorithm
◦ Clusters may change with
scale
◦ Connections may change
with scale
 Filtrations at multiple
resolution settings
 Connections change as
lens zooms in or out
◦ Contains information
about underlying data
structure and
relationships
◦ Hierarchy of Reeb graphs
◦ Topological summary

8. Graph Theory Extensions of
Mapper
 Cluster relationships from
Mapper give an adjacency
matrix and distance metric
◦ Clusters as vertices
◦ Nested hierarchy as edges
◦ Connected/unconnected
components
◦ Centrality of certain points
◦ Bridges linking disparate
clusters
◦ Path lengths between
clusters
 Can apply network
analytics to assess cluster
relationships and
individual connections
across clusters
This is a weighted,
undirected graph!

9. Network Extensions of Multiscale
Mapper
 Graph theory
algorithms applied to
Mapper results dig
deeper into:
◦ Data topology/structure
◦ Nature of individuals’
similarities across
multivariate distribution
 Examine across
different lenses
◦ Hierarchy of networks
connected through
individuals common to
multiple networks
◦ Analyze across slices to
gain deeper insight into
network and underlying
data structures

10. Information from Each
Network Hubs
◦ Direct connection
to many other
clusters
 Betweenness
◦ Non-extremity
measure
 Diversity
◦ Information
contained
 Bridges
◦ Connection
between less-
related
components
 Graph Laplacian
◦ Eigenvectors with
connection/bridge
weights
 Centrality
◦ Weight direct
connections and
bridges for
importance to
network
 Vertices
◦ Clusters at a
particular resolution
 Edges
◦ Connections between
clusters
◦ Individuals common
between clusters
 Levels
◦ Level sets (height
slices) containing one
or more vertices
◦ Individuals bridging
levels

11. Combined Insight of
Extensions
 Multiple resolutions
◦ Cluster hierarchy
 Evolving cluster structure
 More complete picture of
individual classifications
◦ Network hierarchy
 Evolving network structure
 More complete picture of
cluster relationships and
structure
 More complete picture of
individual connections

12. Example Demonstration
 Demo dataset of 7th grade SAT
scores
 Group-level data mining of results
Transition
Transition
Emergence of
subgroups
Split into
two distinct
groups

13. Individual Mining Results
 Map back to individuals
◦ Bridging individuals
 Transition between clusters
 Multivariate cut-off scores
determination
◦ Isolated individuals
 Outliers and outlier groups
 Unique response or predictors
subsets
◦ Consistently clustered
individuals
 Cohesive subgroups in data
 Underlying similarity of
predictors or response

14. Conclusion
New method ameliorates some of the issues
with clustering methods
◦ Robust
◦ Works in high dimensions
◦ Captures connectedness
◦ Stable
◦ Provides hierarchy
◦ Quantify relationships