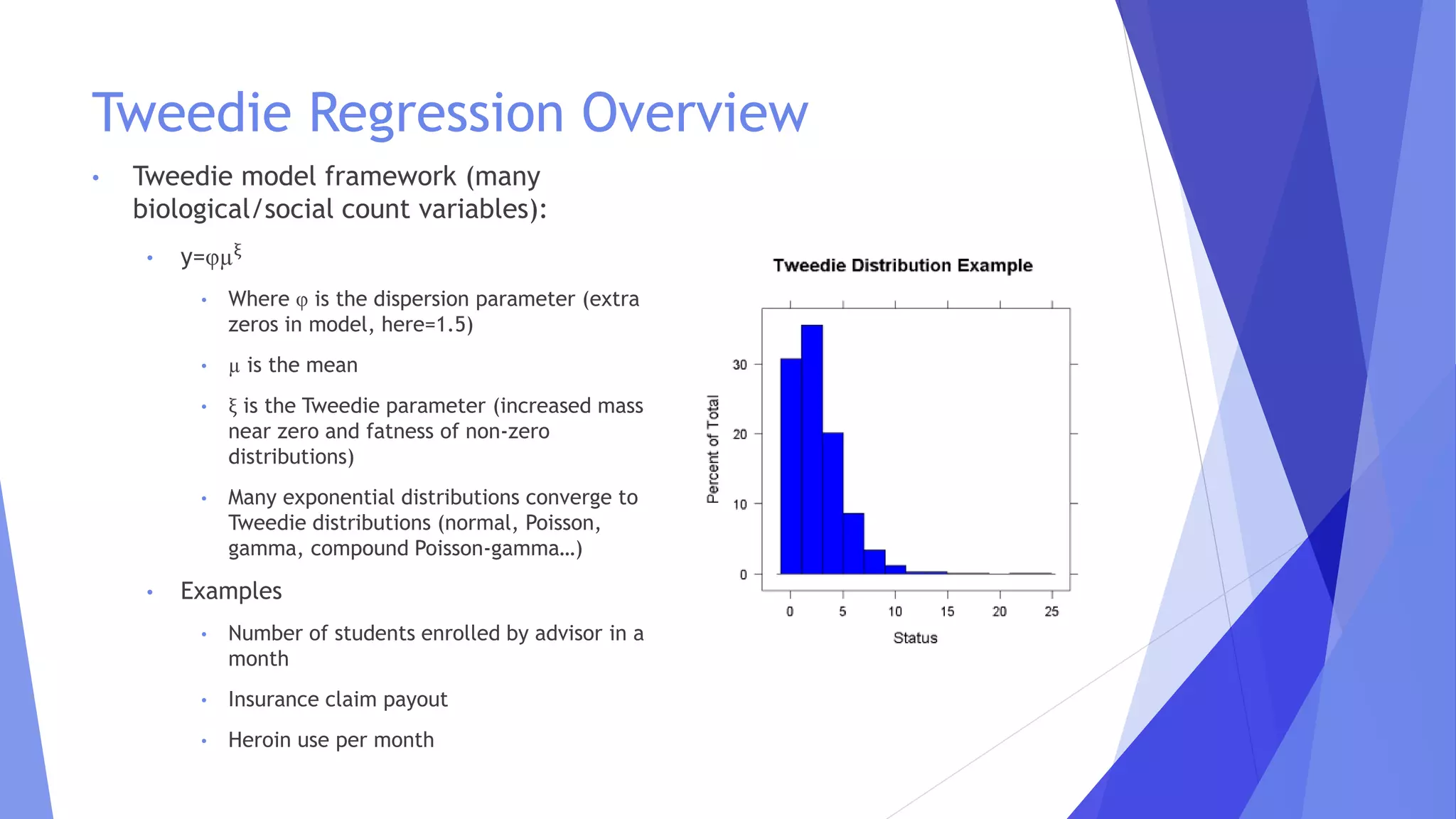
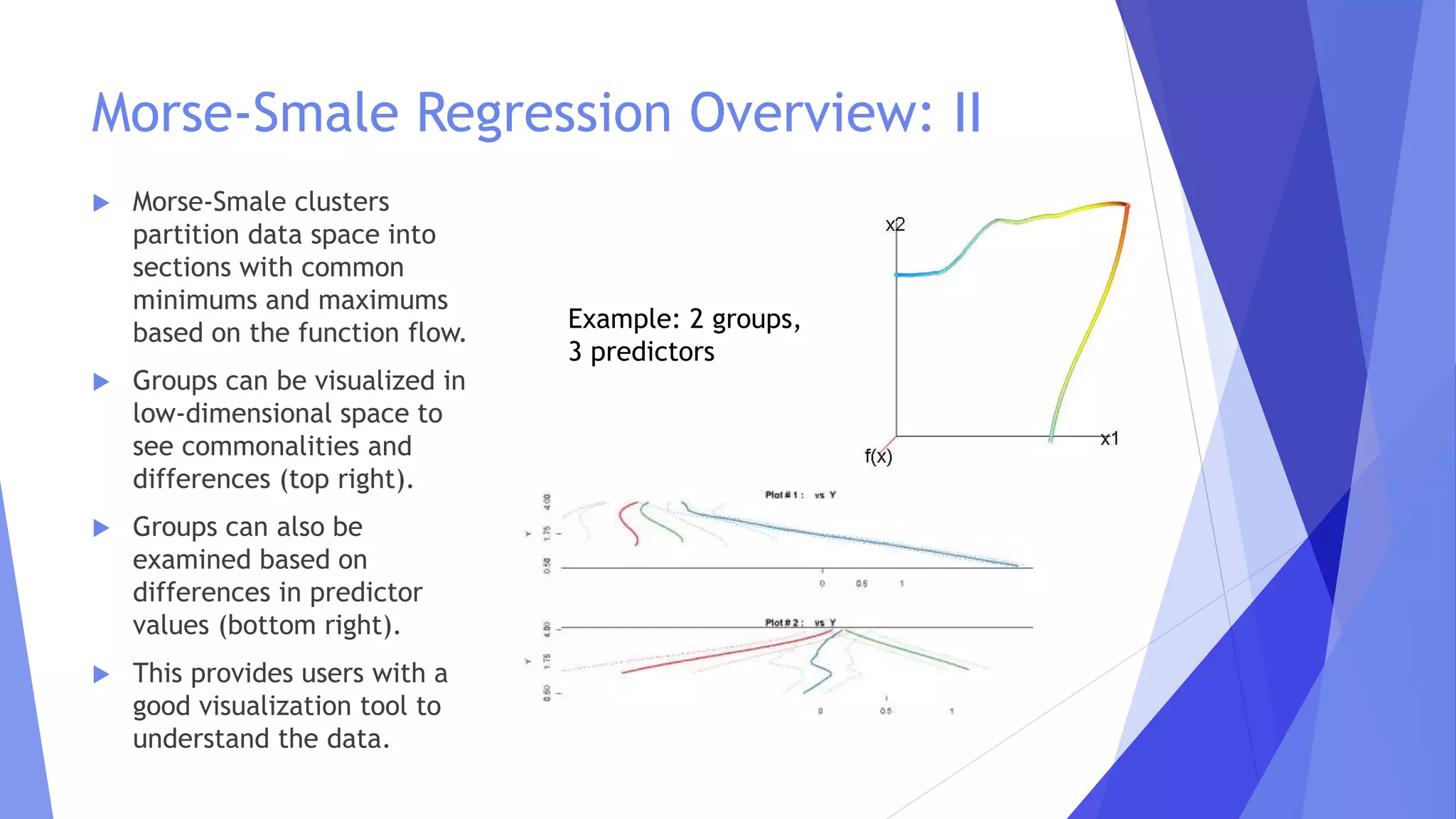
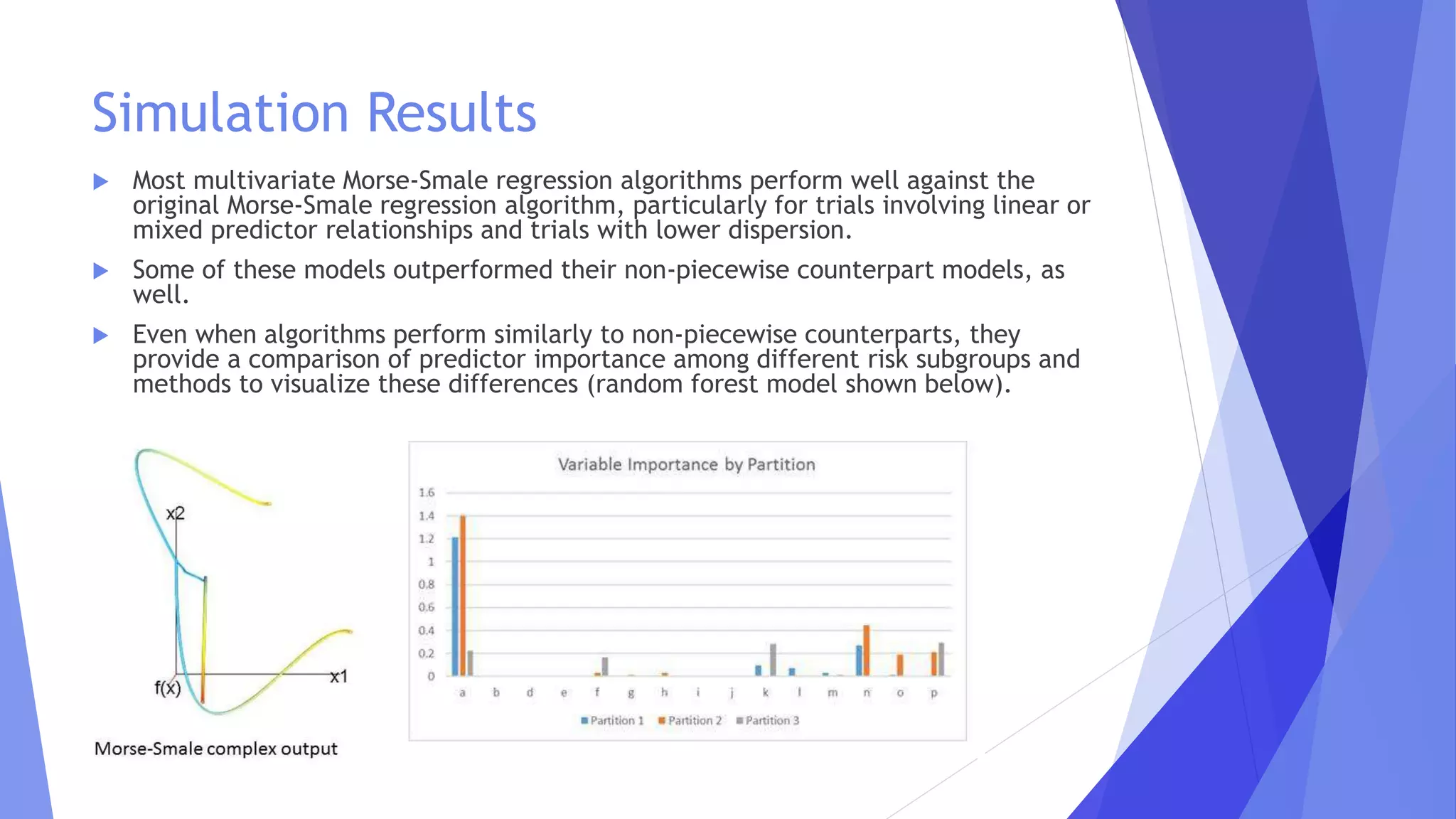
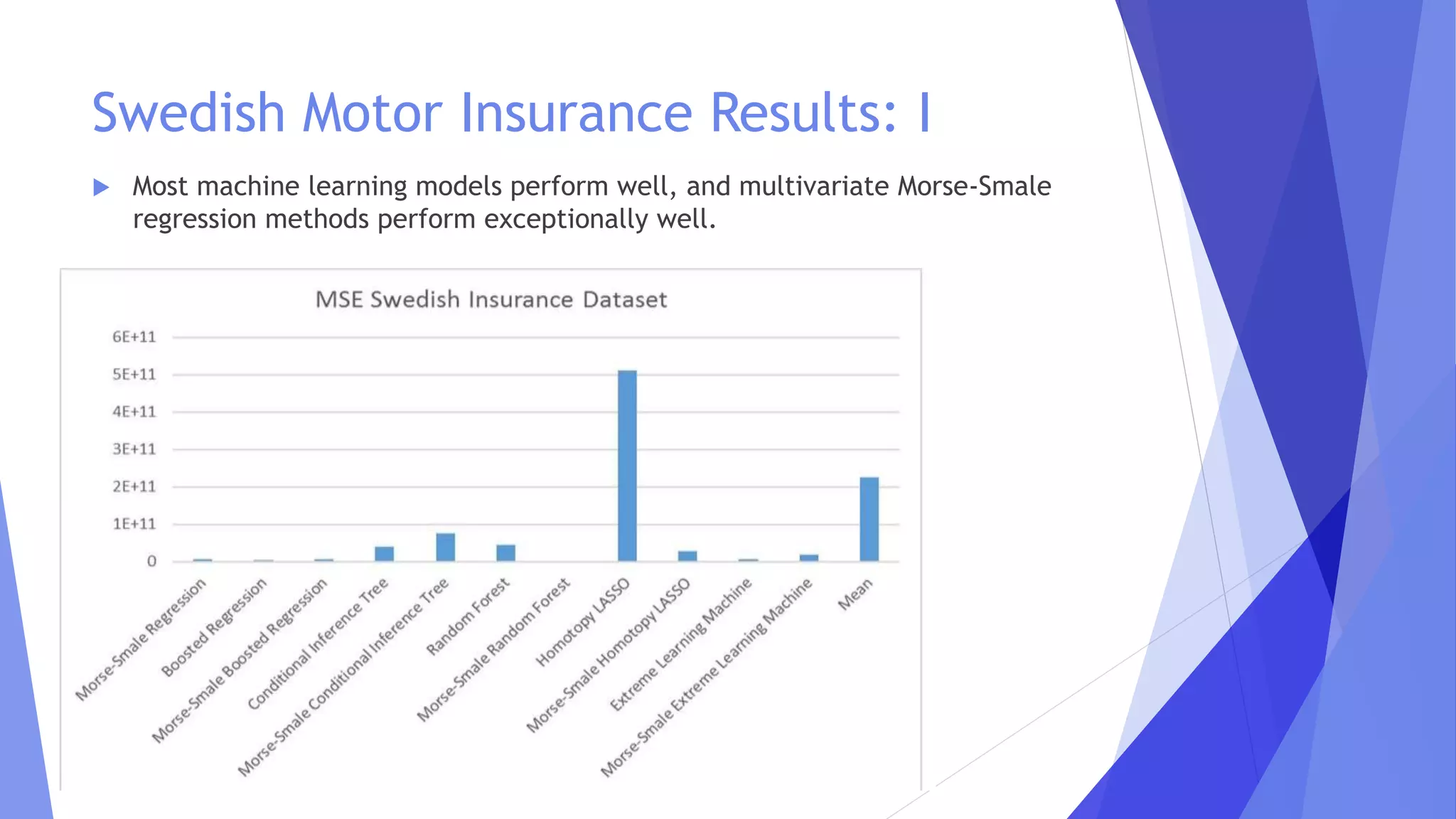
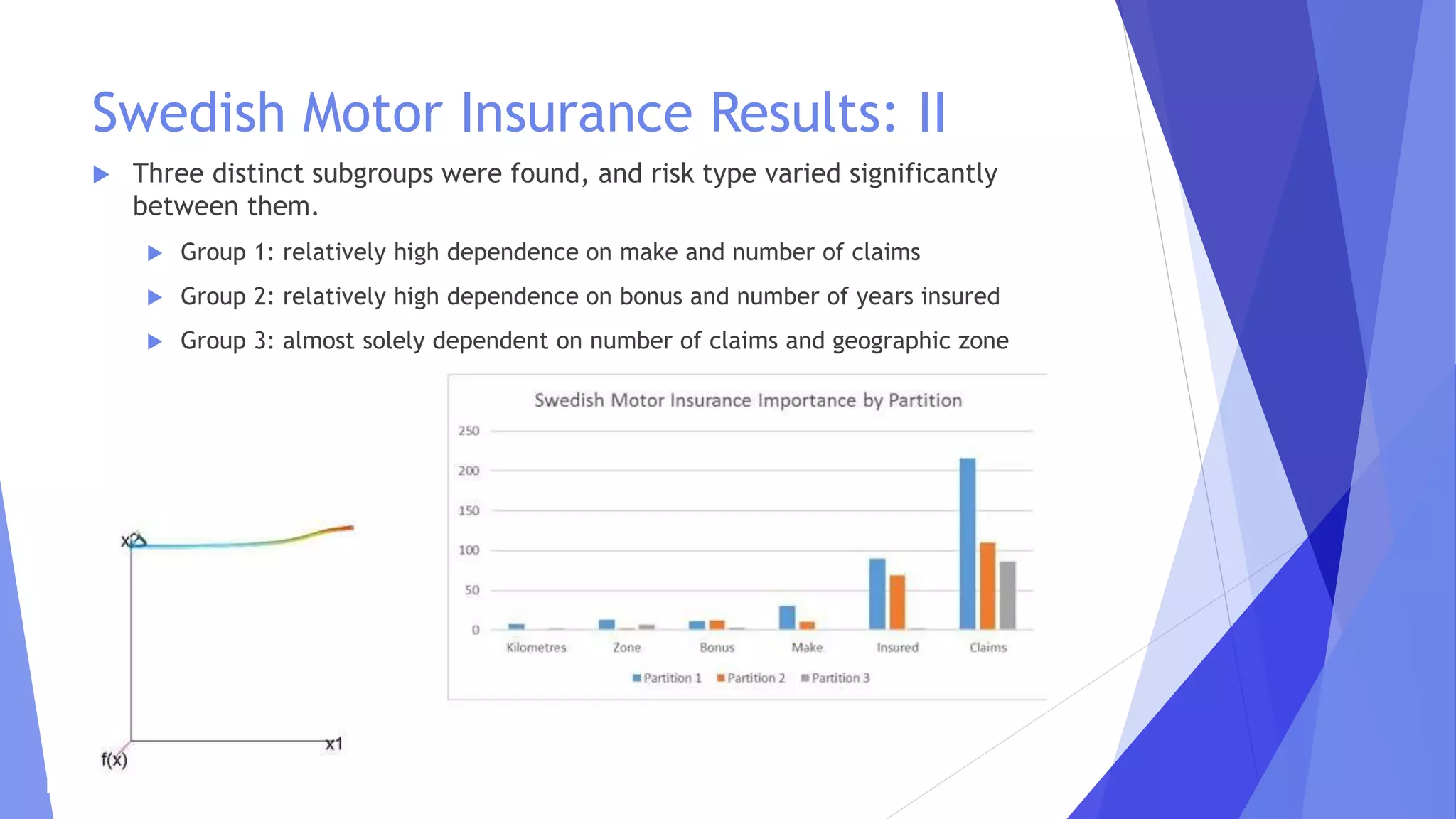
This document discusses the extensions of Morse-Smale regression for risk modeling, emphasizing the method's effectiveness in capturing complex risk types and subgroup variations. The use of machine learning and Tweedie regression is explored, highlighting their advantages in modeling insurance claims and understanding risk structure. Results from simulations and application to Swedish motor insurance indicate that multivariate Morse-Smale regression models perform well and provide valuable insights into risk differentiation.

1. Morse-Smale Regression
Extensions for Risk
Modeling
Colleen M. Farrelly

2. Introduction
 Subgroups are ubiquitous in scientific research and actuarial science.
 Risk is not uniform.
 Risk types can vary in degree and kind, and high risk on some factors are not as
high risk overall as lower risk on other factors.
 Piecewise regression is one method that can accurately capture this
phenomenon.
 Morse-Smale regression is a topologically-based piecewise regression method
that has shown promise on various Tweedie-distributed outcomes, including
common distributions used in modeling risk.
 This method currently employs elastic net and generalized linear modeling to fit
the regression pieces to Morse-Smale-complex-based partitions.
 Many machine learning extensions of regression exist and can capture multivariate
trends in the data, which is a limitation of both elastic net and generalized linear
modeling.
 Extending Morse-Smale regression to machine-learning-based models can
potentially improve accuracy and understanding of risk.

3. Tweedie Regression Overview
• Tweedie model framework (many
biological/social count variables):
• y=φµξ
• Where φ is the dispersion parameter (extra
zeros in model, here=1.5)
• µ is the mean
• ξ is the Tweedie parameter (increased mass
near zero and fatness of non-zero
distributions)
• Many exponential distributions converge to
Tweedie distributions (normal, Poisson,
gamma, compound Poisson-gamma…)
• Examples
• Number of students enrolled by advisor in a
month
• Insurance claim payout
• Heroin use per month

4. Morse-Smale Regression Overview: I
 To build intuition:
 Imagine a soccer player kicking a ball on the ground of a hilly field to explore the
field.
 The high and low points (maxima and minima) determine where the ball will come to rest.
 These paths of the ball define which parts of the field share common hills and valleys.
 These paths are actually gradient paths defined by height on the field’s topological
space.
 The spaces they define are the Morse-Smale complex of the field, partitioning it
into different regions (clusters).

5. Morse-Smale Regression Overview: II
 Morse-Smale clusters
partition data space into
sections with common
minimums and maximums
based on the function flow.
 Groups can be visualized in
low-dimensional space to
see commonalities and
differences (top right).
 Groups can also be
examined based on
differences in predictor
values (bottom right).
 This provides users with a
good visualization tool to
understand the data.
Example: 2 groups,
3 predictors

6. Extending Morse-Smale Regression
 Multivariate algorithms to fit partitioned regression models
 Random forest
 Bagged ensemble of tree models
 Akin to combining novel summaries of a class randomly assigned a few chapters
 Boosted regression
 Iteratively added model of main effects and interaction terms
 Akin to guessing a puzzle’s picture by adding key pieces until the picture is mostly there
 Homotopy LASSO
 Extends penalized regression model (LASSO) through homotopy estimation methods
 Akin to a blind-folded person navigating around obstacles between two set points by
following a rope
 Conditional inference tree
 Tree method that partitions space by assessing covariate independence
 Extreme learning machine
 Single-layer feed-forward neural networks based on random mapping between layers
 Has universal approximation properties

7. Simulation and Swedish Motor Insurance
 Simulation
 Simulation design parameters
 4 true predictors, 11 noise variables
 Sample size set to 10,000
 Outcome Tweedie-distributed, with Tweedie parameter varying (1, 1.5, 2) and dispersion
(1, 2, 4)
 Nature of predictor relationships varied (4 main effects, 2 interaction effects, or a
combination of 2 main effects and 1 interaction effect)
 Each trial was run 10 times with a 70/30 training/test split.
 Mean square error (MSE) was used to assess model accuracy.
 Swedish 3rd Party Motor Insurance 1977
 2182 observations with 6 predictors (kilometers traveled per year, geographic zone,
bonus, car model make, number of years insured, total claims)
 MSE assessed for all models based on 70/30 training/test split

8. Simulation Results
 Most multivariate Morse-Smale regression algorithms perform well against the
original Morse-Smale regression algorithm, particularly for trials involving linear or
mixed predictor relationships and trials with lower dispersion.
 Some of these models outperformed their non-piecewise counterpart models, as
well.
 Even when algorithms perform similarly to non-piecewise counterparts, they
provide a comparison of predictor importance among different risk subgroups and
methods to visualize these differences (random forest model shown below).

9. Swedish Motor Insurance Results: I
 Most machine learning models perform well, and multivariate Morse-Smale
regression methods perform exceptionally well.

10. Swedish Motor Insurance Results: II
 Three distinct subgroups were found, and risk type varied significantly
between them.
 Group 1: relatively high dependence on make and number of claims
 Group 2: relatively high dependence on bonus and number of years insured
 Group 3: almost solely dependent on number of claims and geographic zone

11. Conclusions
 Multivariate Morse-Smale regression models typically:
 Outperform the original Morse-Smale regression algorithm
 Perform comparably to the non-partitioned models built with the same machine
learning algorithm.
 Multivariate Morse-Smale regression models provide subgroup-based analytics
capabilities and differentiated risk structure abilities that can help actuaries:
 Better understand risk
 Create models based on insurance policy risk groups (as well as risk level)
 Visualize this process to help others within the industry understand the models
(less black-box)
 However, some black-box algorithms perform better on Tweedie regression
problems (particularly Farrelly, 2017, KNN regression ensembles); these
methods don’t allow for visualization or comparison of risk factors.
 Large sample sizes are needed for good performance, but most insurance
datasets are large enough to circumvent potential convergence issues.

12. References
 Talk is a summary of:
 Farrelly, C. M. (2017). Extensions of Morse-Smale Regression with Application to
Actuarial Science. arXiv preprint arXiv:1708.05712.—Accepted Dec 2017 for
publication by Casualty Actuarial Society
 Selected references from 2017 Farrelly paper:
 De Jong, P., & Heller, G. Z. (2008). Generalized linear models for insurance data
(Vol. 10). Cambridge: Cambridge University Press.
 Farrelly, C. M. (2017). KNN Ensembles for Tweedie Regression: The Power of
Multiscale Neighborhoods. arXiv preprint arXiv:1708.02122.
 Gerber, S., Rübel, O., Bremer, P. T., Pascucci, V., & Whitaker, R. T. (2013). Morse–
smale regression. Journal of Computational and Graphical Statistics, 22(1), 193-
214.
 McZgee, V. E., & Carleton, W. T. (1970). Piecewise regression. Journal of the
American Statistical Association, 65(331), 1109-1124.
 Tomoda, K., Morino, K., Murata, H., Asaoka, R., & Yamanishi, K. (2016). Predicting
Glaucomatous Progression with Piecewise Regression Model from Heterogeneous
Medical Data. HEALTHINF, 2016.