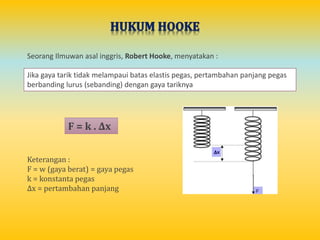
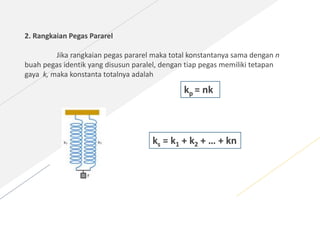
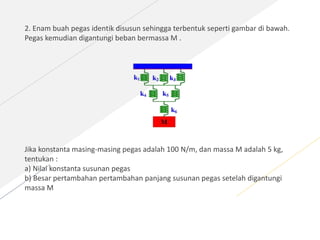
Dokumen ini menjelaskan tentang konsep tegangan, regangan, dan modulus elastisitas dalam fisika, serta aplikasi teori ini pada pegas. Istilah-istilah seperti tegangan (σ), regangan (e), dan hukum Hooke diperkenalkan untuk menggambarkan perilaku benda elastis. Selain itu, terdapat contoh perhitungan untuk menentukan nilai-nilai tersebut berdasarkan kondisi spesifik pegas.

4. Tegangan (stress) didefinisikan sebagai gaya yang diperlukan oleh
benda untuk kembali ke bentuk semula. Tegangan diberi simbol σ (dibaca
sigma).
Secara matematis dapat ditulis sebagai berikut.
Keterangan :
F : Besar gaya tekan/tarik (N)
A : Luas penampang (m2)
σ : Tegangan (N/m2 atau Pa)
Bila dua buah kawat dari bahan yang sama tetapi luas
penampangnya berbeda diberi gaya, maka kedua kawat tersebut akan
mengalami tegangan yang berbeda. Kawat dengan penampang kecil
mengalami tegangan yang lebih besar dibandingkan kawat dengan
penampang lebih besar

5. Regangan (strain) didefinisikan sebagai perbandingan antara
penambahan panjang benda ∆L terhadap panjang mula-mula Lo.
Regangan dirumuskan sebagai berikut.
Keterangan:
e : Regangan
∆𝐿 : Pertambahan panjang (m)
Lo : Panjang mula-mula (m)
Makin besar tegangan pada sebuah benda, makin besar juga regangannya.
Karena pertambahan panjang ∆L dan panjang awal Lo adalah besaran yang
sama, regangan (e) tidak memiliki satuan atau dimensi

6. Modulus Elastisitas (E) adalah perbandingan antara tegangan (σ)
dan regangan (e) dari suatu benda.
Secara matematis ditulis seperti berikut.
Keterangan :
E : Modulus Elastis (N/m2 atau Pa)
σ : Tegangan (N/m2 atau Pa)
e : Regangan
Modulus elastis bergantung hanya pada jenis zat dan tidak pada ukuran atau
bentuknya.

7. Sebuah bahan elastis silinder dengan panjang 20 cm dan
luas penampang 5 cm2 dalam keadaan tergantung bebas.
Pada penampang yang bebas ditarik dengan gaya 2
Newton sehingga bahan bertambah panjang 1 cm.
Hitunglah:
a. Tegangan (stress) dari bahan elastis tersebut
b. Regangan (strain) dari bahan elastis tersebut
c. Modulus elastis bahan tersebut

8. FR
Diketahui :
Lo = 20 cm = 2 x 10-2 m
∆𝐿 = 1 cm = 1 x 10-2 m
A = 5 cm2 = 5x 10-4 m
F = 2 N
Ditanya :
𝜎 ?
𝑒?
E ?
Jawab :
𝜎 =
𝐹
𝐴
=
2 N
5x 10−4 m
= 4.000 atau 4x103 N/m2
𝑒 =
∆L
𝐿𝑜
=
1 x 10−2 m
20 x 10−2 m
= 0.05 atau 5x10-2 m
𝐸 =
𝜎
𝑒
=
4000 𝑁/𝑚2
5𝑥10−2 𝑚
= 800 x 102 = 80.000 Pa

9. Benda berbentuk spiral yang terbuat dari logam disebut pegas.
Pegas sendiri memiliki elastisitas. Salah satunya tokoh yang memiliki
elastisitas adalah Reed Richards, seorang manusia karet yang elastis.
Ternyata pegas juga sama seperti Reed Richards, elastis. Apa sih elastis itu?
Elastis adalah kemampuan benda untuk kembali ke bentuk semula setelah
gaya yang bekerja padanya dihilangkan.
Ketika pegas ditarik yang berarti ada gaya luar yang bekerja maka ia akan
memanjang. Ketika gaya luar itu dihilangkan ia akan kembali ke bentuk
semula sifat elastis.

10. Jika gaya tarik tidak melampaui batas elastis pegas, pertambahan panjang pegas
berbanding lurus (sebanding) dengan gaya tariknya
Seorang Ilmuwan asal inggris, Robert Hooke, menyatakan :
F = k . Δx
Keterangan :
F = w (gaya berat) = gaya pegas
k = konstanta pegas
Δx = pertambahan panjang

11. Sebuah pegas yang diberi gaya entah itu ditarik atau ditekan akan
memiliki energi potensial (energi karena kedudukan). Usaha yang dilakukan
oleh gaya F untuk menarik sebuah pegas sehingga bertambah panjang
sebesar x besarnya sama dengan perubahan energi potensial dari pegas.
Coba sobat hitung amati grafik hubungan gaya F dengan delta x berikut :
Luasan di bawah yang diarsir merupakan
usaha = perupahan energi potensial. Jadi
untuk menghitung energi potensial bisa
dirumuskan

12. 1. Seorang anak yang massanya 50 kg bergantung pada ujung sebuah pegas
sehingga pegas bertambah panjang 10 cm. Tetapan pegas bernilai...
A. 500 N/m
B. 5 N
C. 50 N/m
D. 20 N/m
E. 5000 N/m
Diketahui :
m = 50 kg
Δx = 10 cm = 0,1 m
Ditanya :
k = ?
Jawab :
F = mg
kΔx = F
kΔx = mg
k (0,1) = 50(10)
k = 5000 N/m

13. 2. Sebuah balok yang bermassa 225 gram digantungkan pada pegas sehingga
pegas bertambah panjang 35 cm. Berapa panjang pegas mula-mula jika
konstanta pegas 45 N/m ?
Di ketahui :
m = 225 gram = 0,225 kg
X2 = 35 cm
K : 45 N/m
Ditanya :
X1 = ?
Jawab :
F = k . Δx
F = w = m. g = 0.225 kg . 10s/m2 = 2.25
N
F = k . Δx
2.25 N = 45 N/m .Δx
2.25 N / 45 N/m = Δx
0.05 m = Δx
5 cm = Δx
Δx = X2 – X1
5 cm = 35 cm – X1
30 cm = X1
Jadi panjang pegas mula-mula 30 cm.

14. 3. Untuk meregangkan sebuah pegas sebesar 4 cm diperlukan usaha sebesar
0,16 J. Untuk meregangkan pegas sebesar 2 cm maka diperlukan gaya
sebesar....
a. 0,8 N
b. 1,6 N
c. 2,4 N
d. 3,2 N
e. 4,0 N
Diketahui:
X1 = 4 cm = 0,04 m
W = 0,16 J
X2 = 2 cm = 0,02 m
Ditanya: F (gaya dari pegas ke2) ?
Jawab:
W = 1/2. k . X1 ²
0,16 = 1/2. k. 0,04²
0,16 = 1/2. k. 0,0016
0,32 = k. 0,0016
k = 0,32/0,0016
k = 200 N/m
maka, F = k . X2
F = 200. 0,02
F = 4 N (Jawaban: E)

15. FR
Bentuk rangkaian pegas akan menentukan nilai konstanta pegas total yang
akhirnya akan menentukan nilai dari gaya pegas.
1. Rangkaian Pegas Seri
Jika rangkaian seri maka konstanta pegas totalnya adalah jika ada n
pegas identik (konstanta k), maka rumus konstanta totalnya adalah
Kebalikan tetapan pegas pengganti
seri sama dengan total dari kebalikan
tiap-tiap tetapan pegas
ks = k/n

16. 2. Rangkaian Pegas Pararel
Jika rangkaian pegas pararel maka total konstantanya sama dengan n
buah pegas identik yang disusun paralel, dengan tiap pegas memiliki tetapan
gaya k, maka konstanta totalnya adalah
ks = k1 + k2 + … + kn
kp = nk

17. Contoh soal:
1. Sebuah pegas digantung dengan posisi seperti gambar berikut! Pegas kemudian
diberi beban benda bermassa M = 500 gram sehingga bertambah panjang 5 cm.
Tentukan :
a) Nilai konstanta pegas
b) Energi potensial pegas pada kondisi II
c) Energi potensial pegas pada kondisi III ( benda M kemudian ditarik sehingga
bertambah panjang 7 cm)
d) Energi potensial sistem pegas pada kondisi III
e) Periode getaran yang terjadi jika pegas disimpangkan hingga bergetar harmonis
f) Frekuensi getaran pegas

18. Pembahasan
a) Nilai konstanta pegas
Gaya-gaya yang bekerja pada benda M saat kondisi II adalah gaya pegas dengan
arah ke atas dan gaya berat dengan arah ke bawah. Kedua benda dalam kondisi
seimbang.
b) Energi potensial pegas pada kondisi II
c) Energi potensial pegas pada kondisi III ( benda M kemudian ditarik sehingga
bertambah panjang 7 cm)

19. d) Energi potensial sistem pegas pada kondisi III
e) Periode getaran yang terjadi jika pegas disimpangkan hingga bergetar harmonis
f) Frekuensi getaran pegas

20. 2. Enam buah pegas identik disusun sehingga terbentuk seperti gambar di bawah.
Pegas kemudian digantungi beban bermassa M .
Jika konstanta masing-masing pegas adalah 100 N/m, dan massa M adalah 5 kg,
tentukan :
a) Nilai konstanta susunan pegas
b) Besar pertambahan pertambahan panjang susunan pegas setelah digantungi
massa M

21. Pembahasan
a) Nilai konstanta susunan pegas
b) Besar pertambahan pertambahan panjang susunan pegas setelah
digantungi massa M