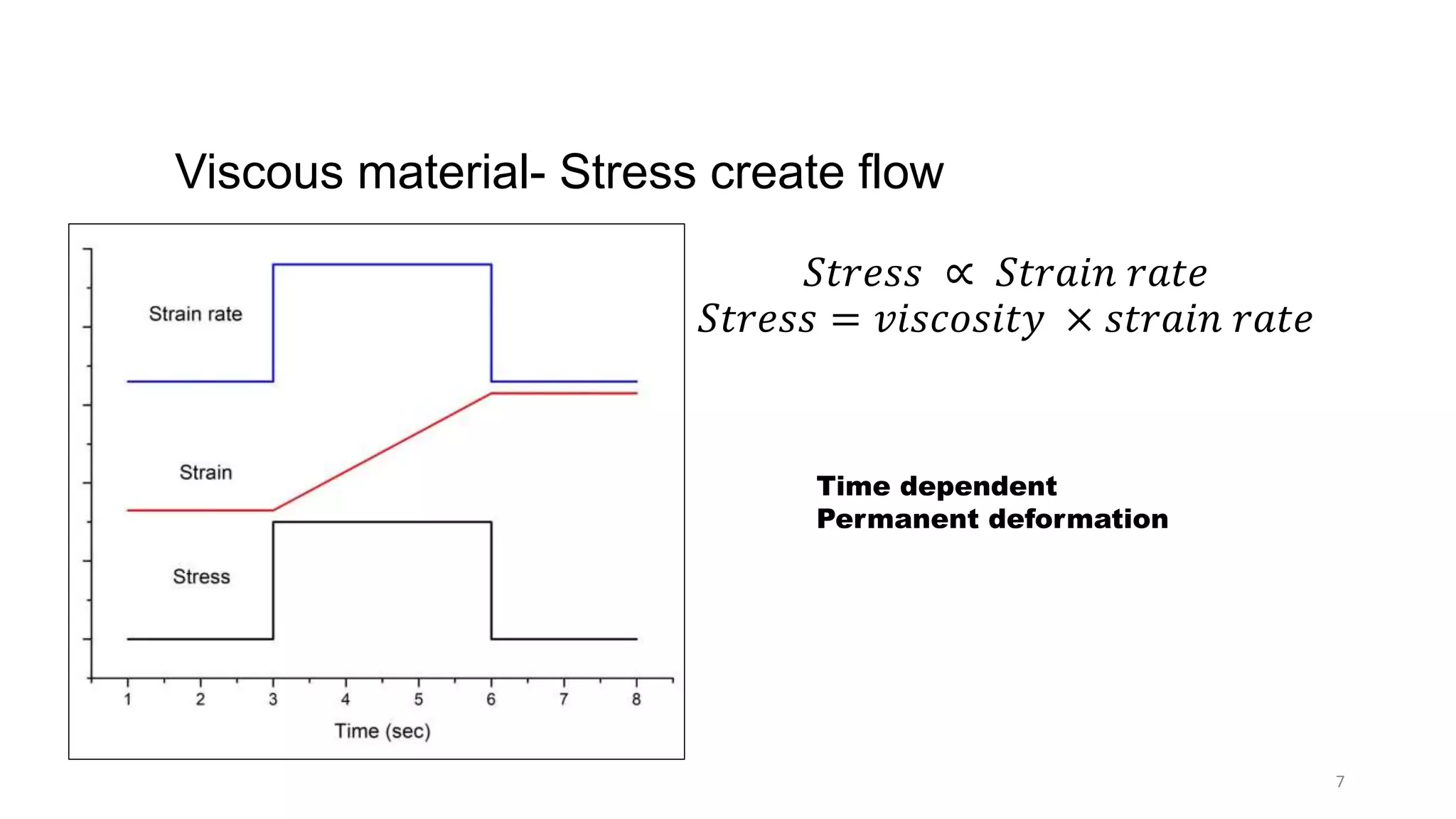
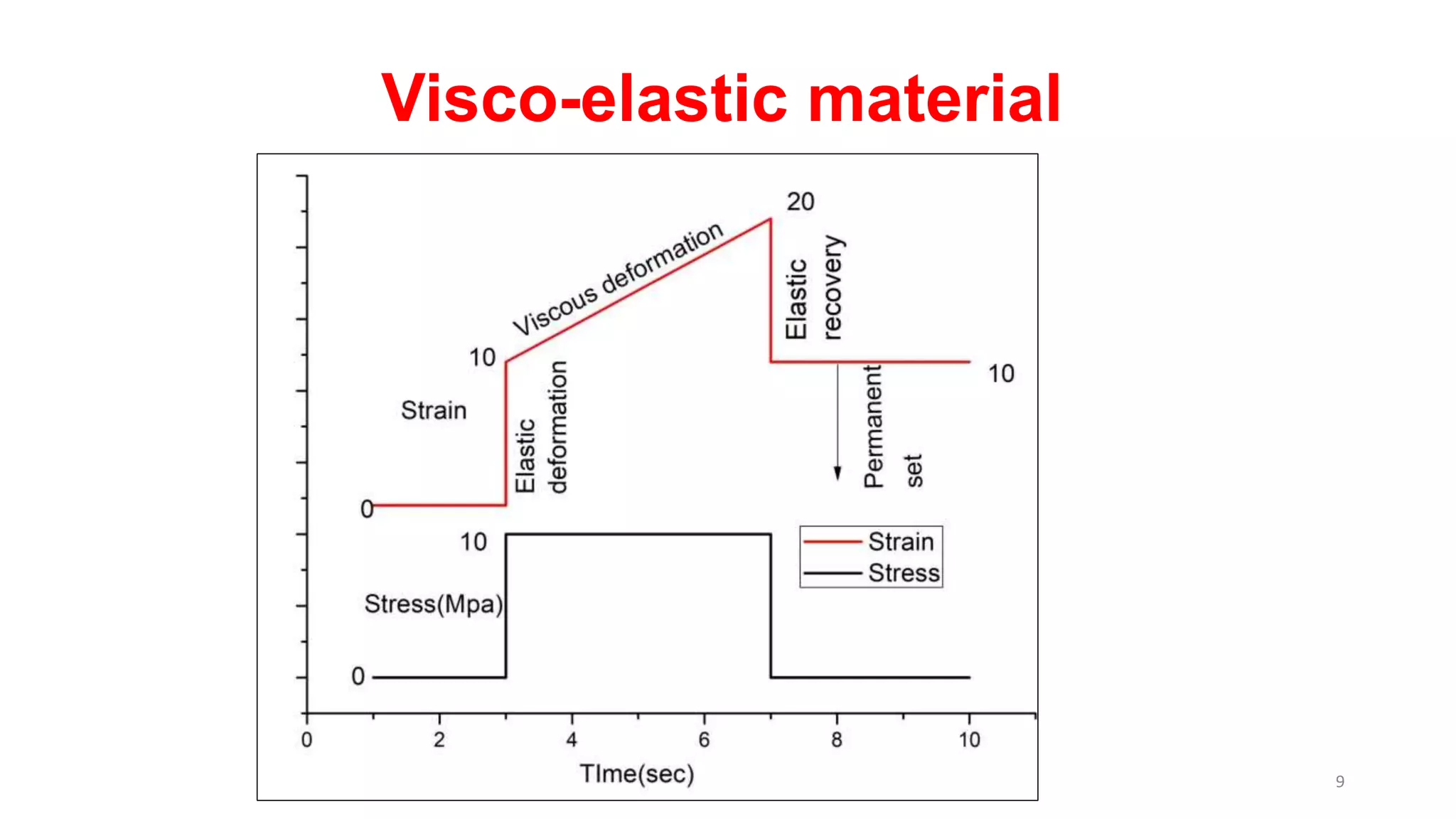
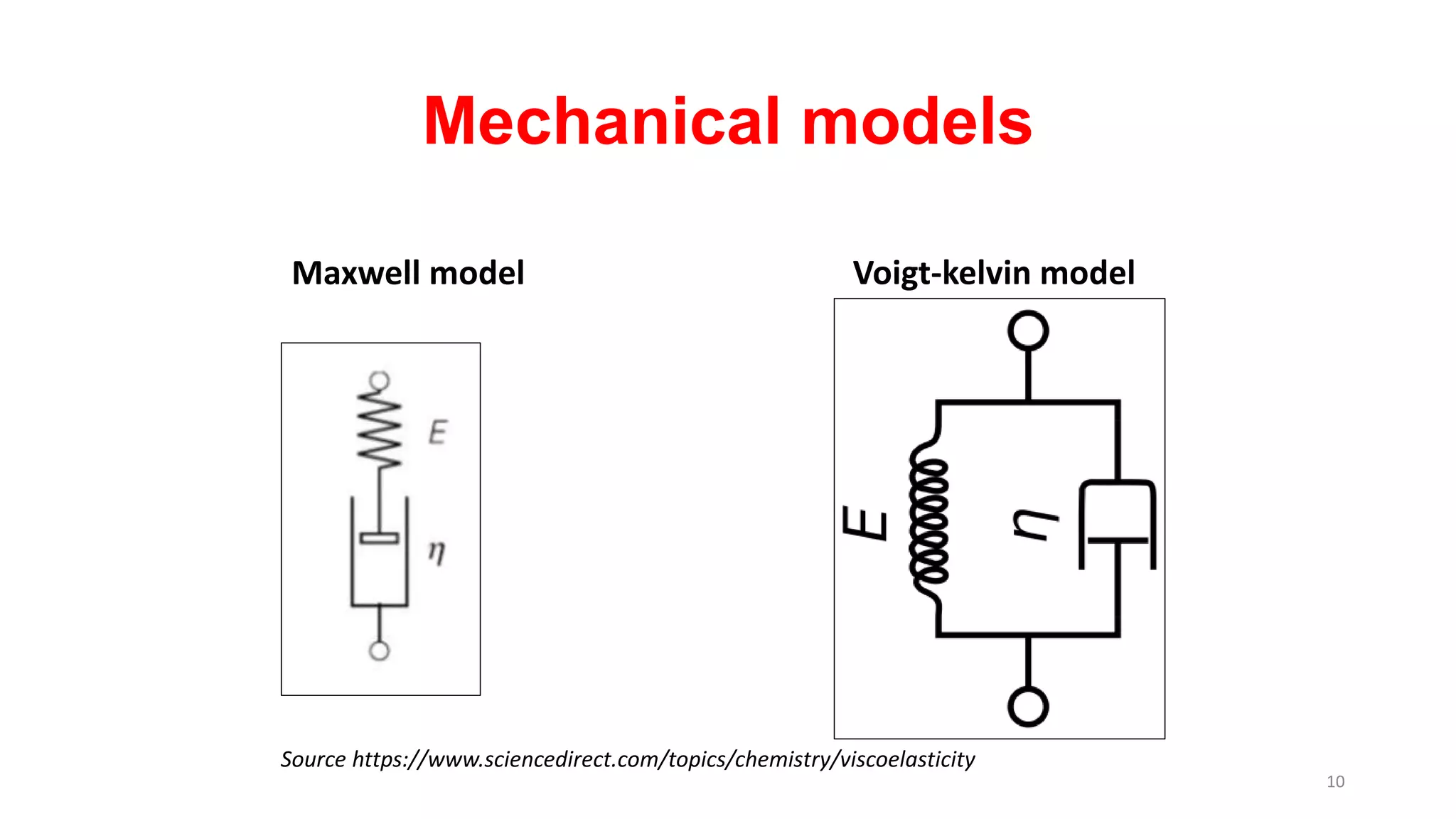
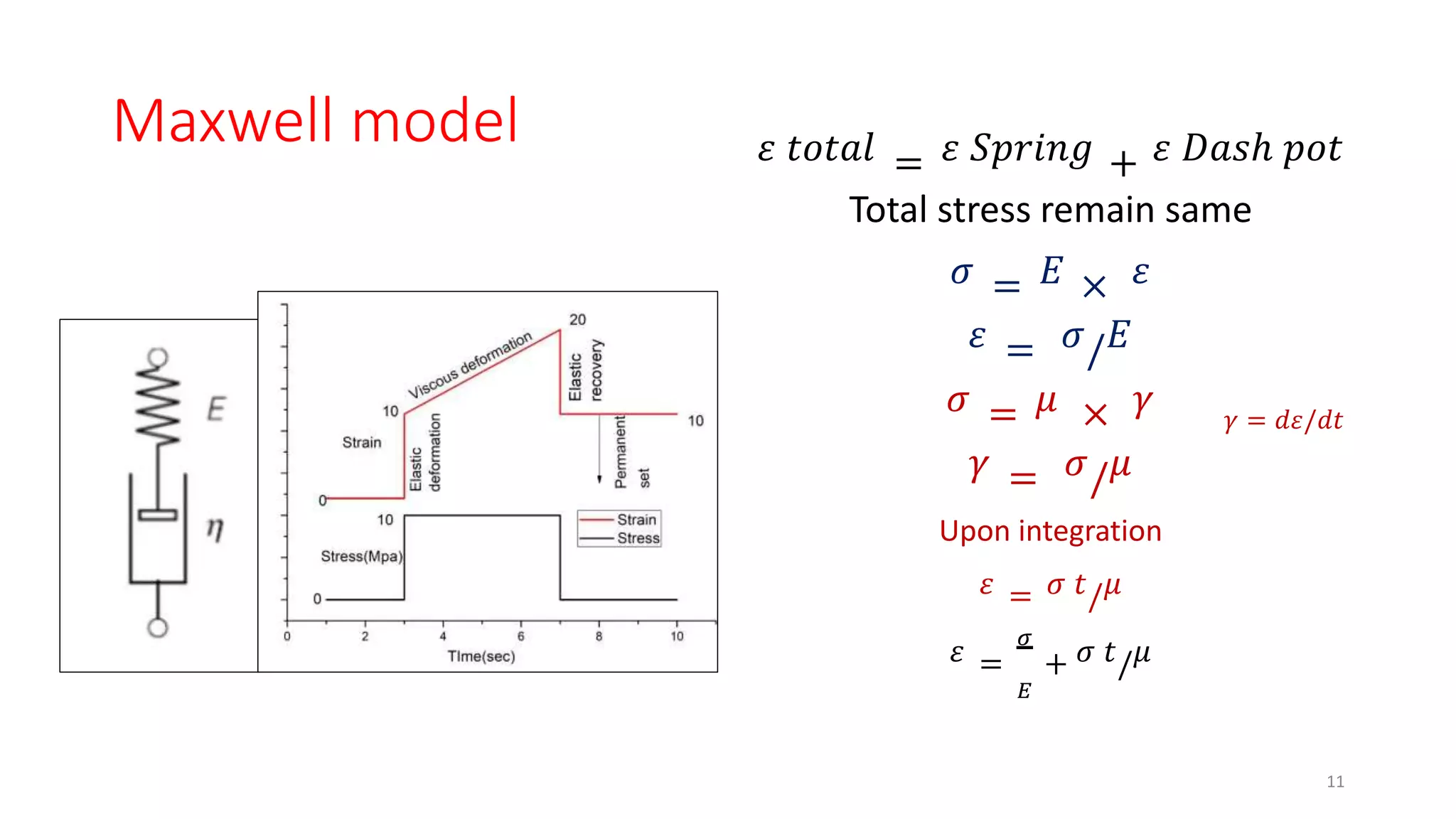
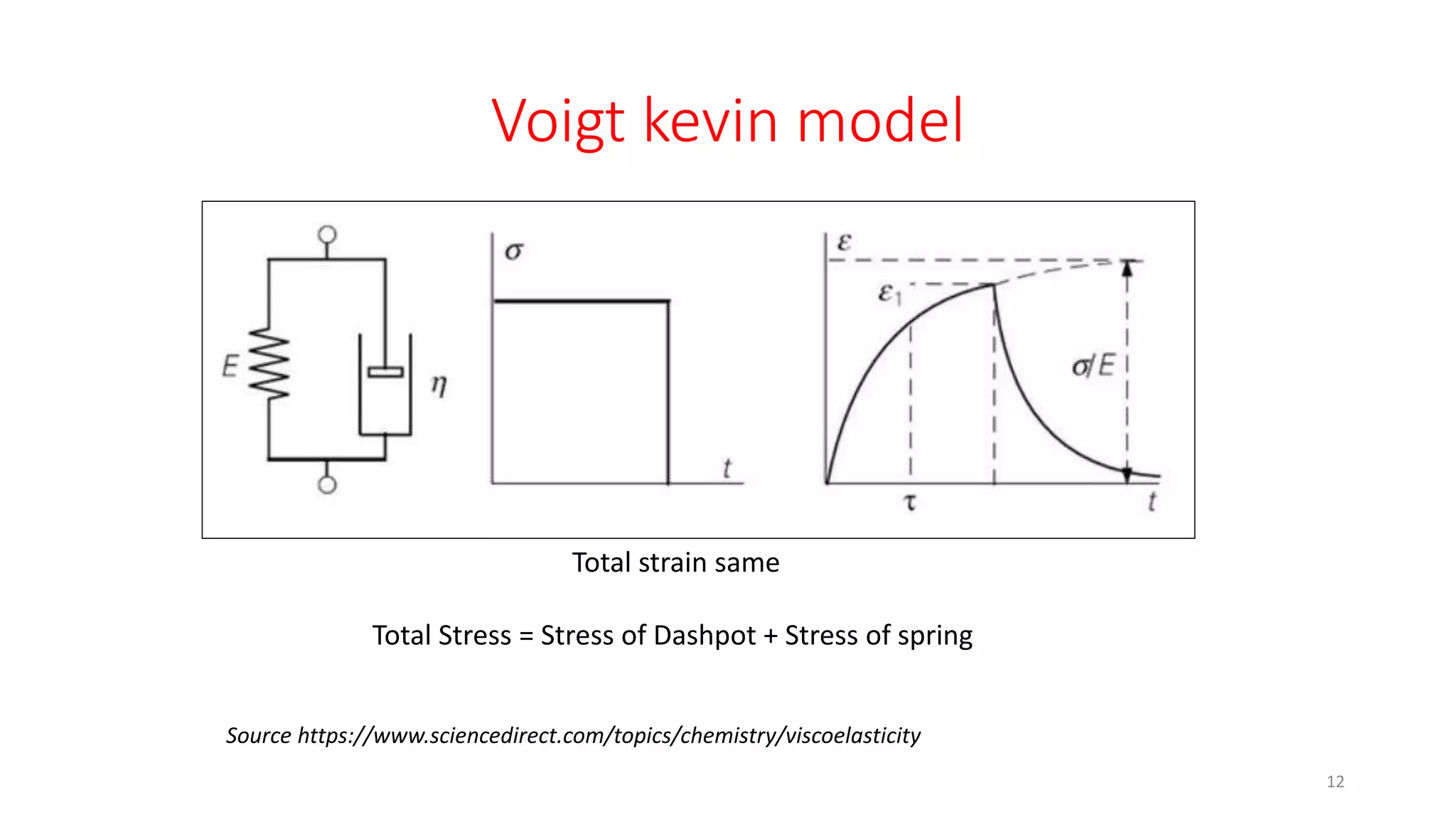
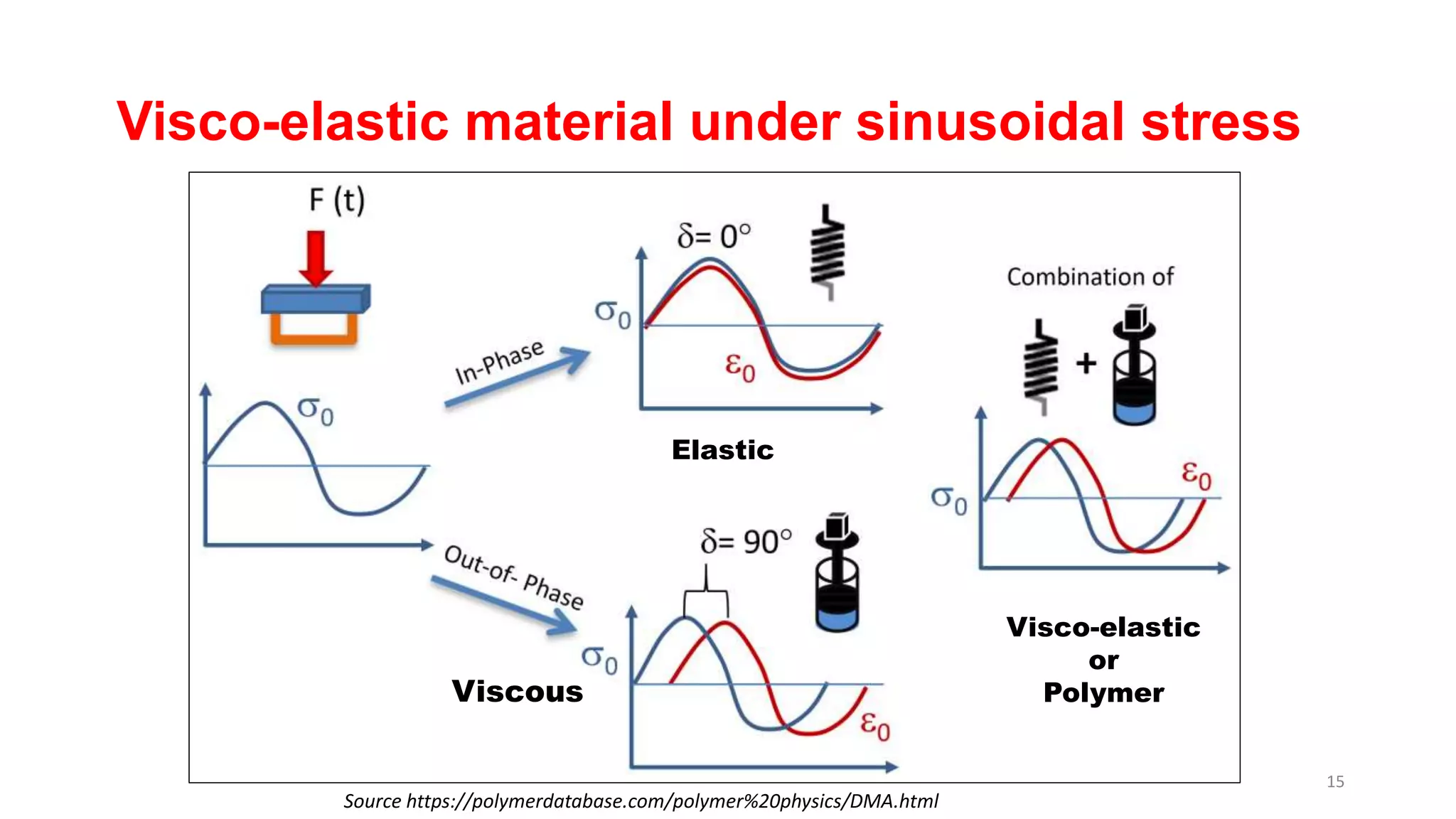
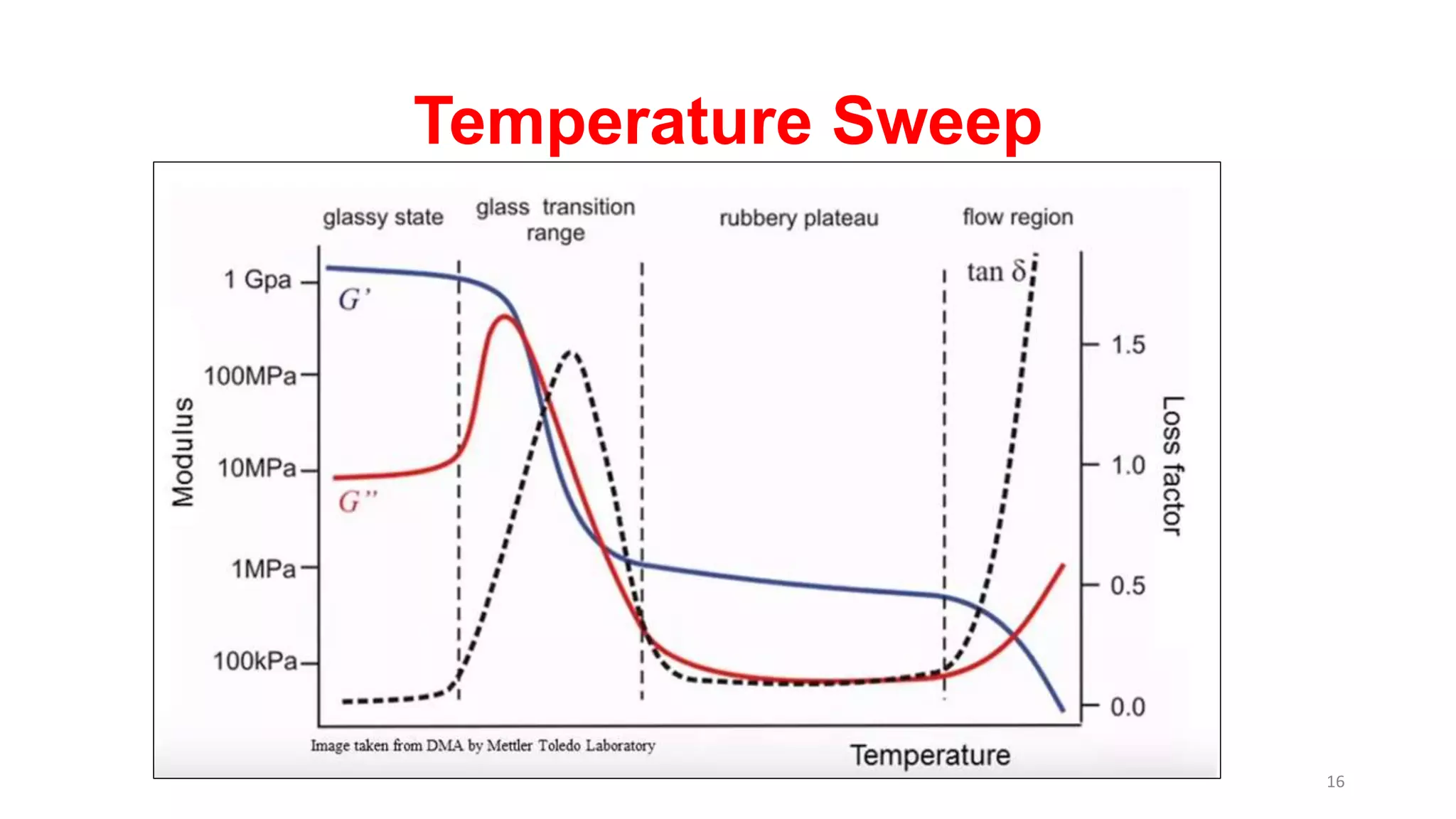
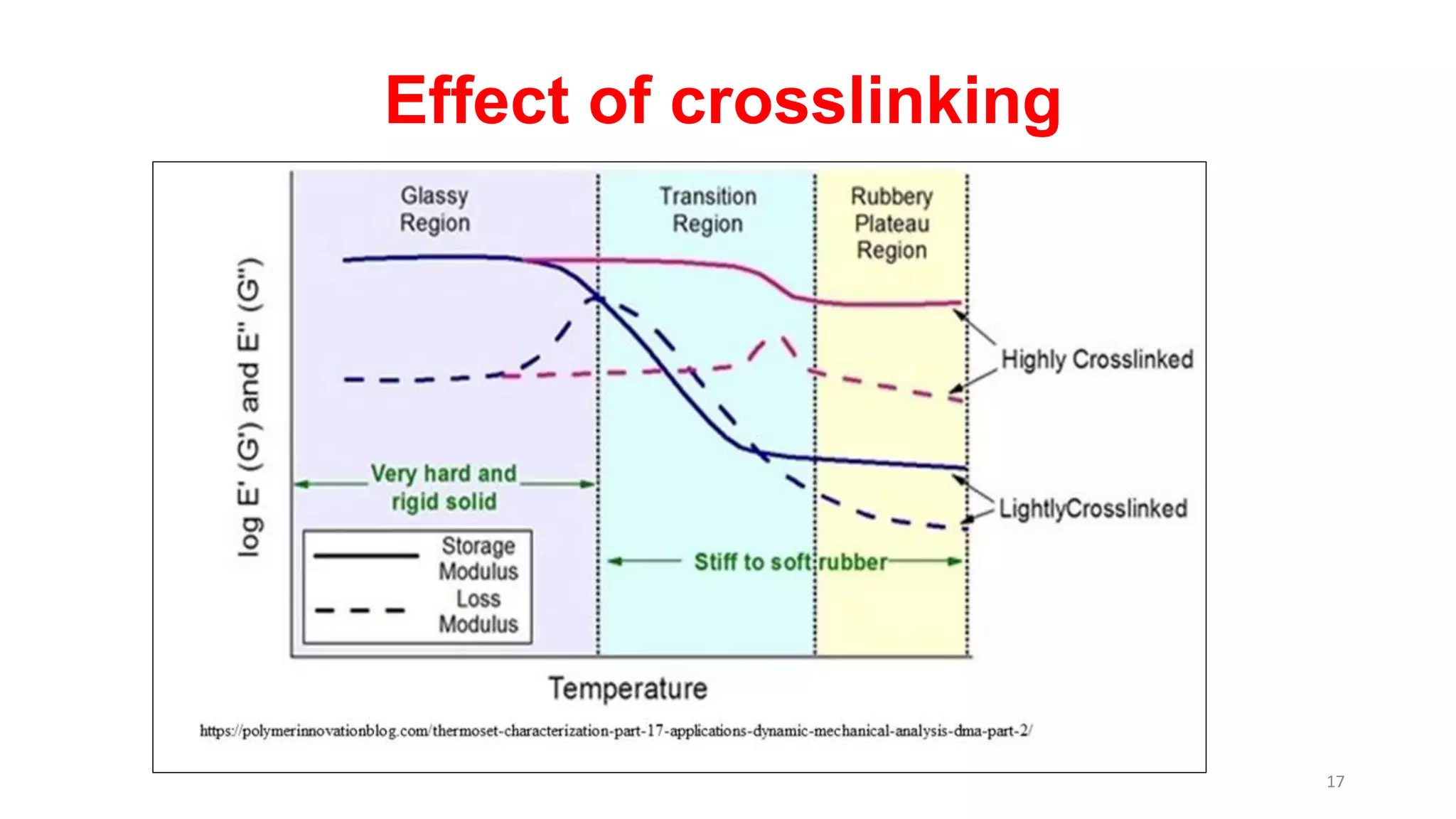
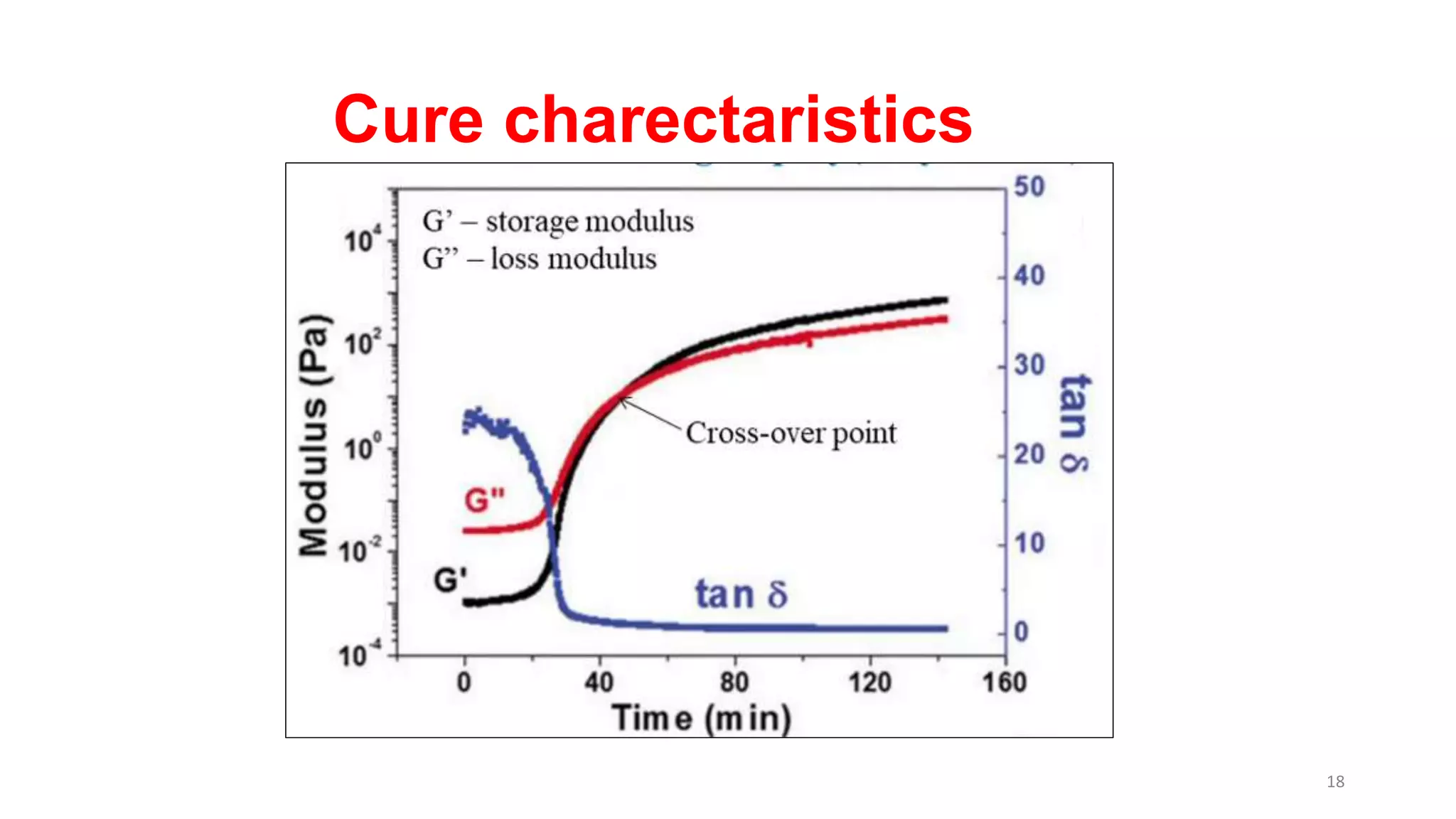
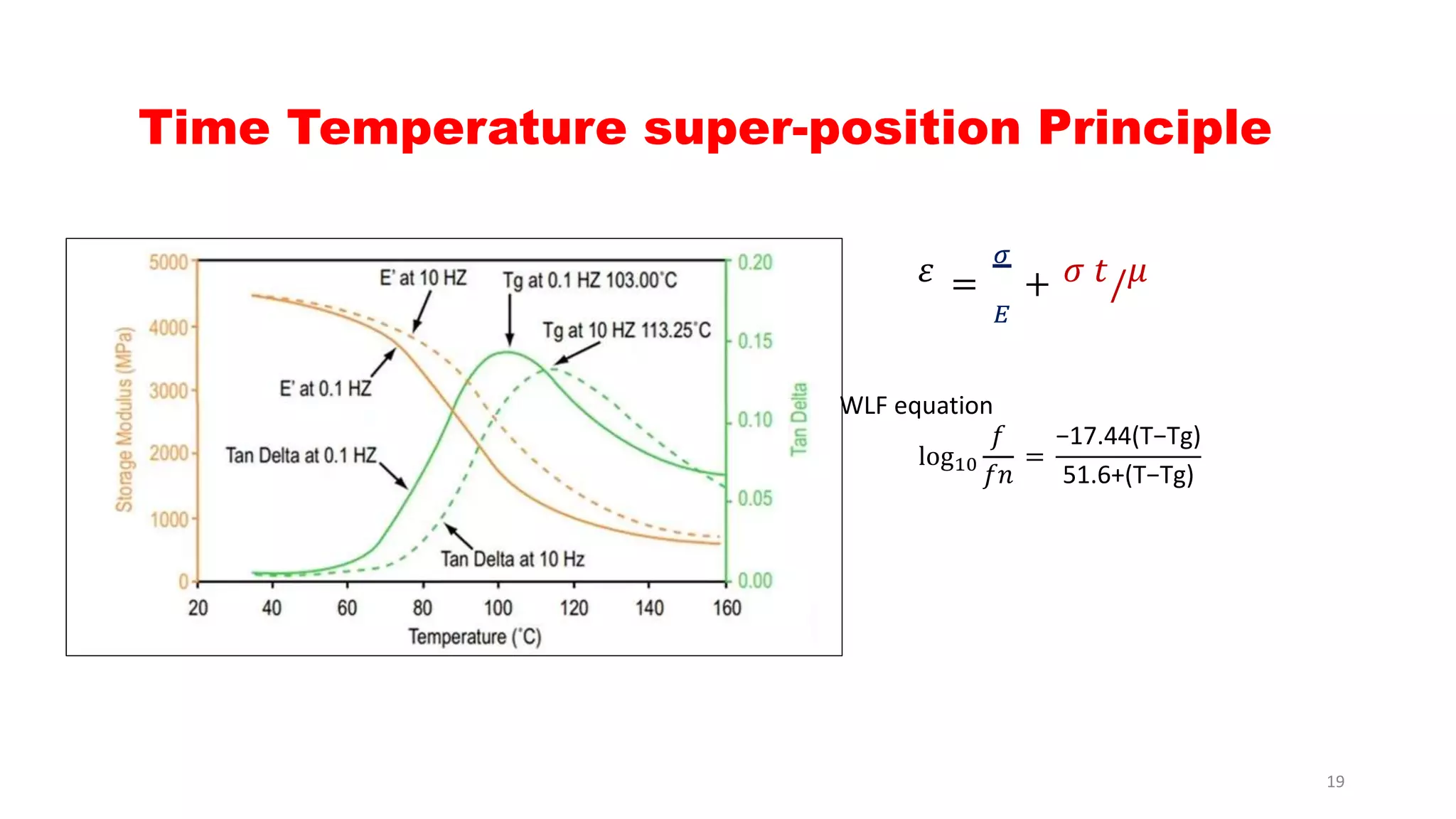
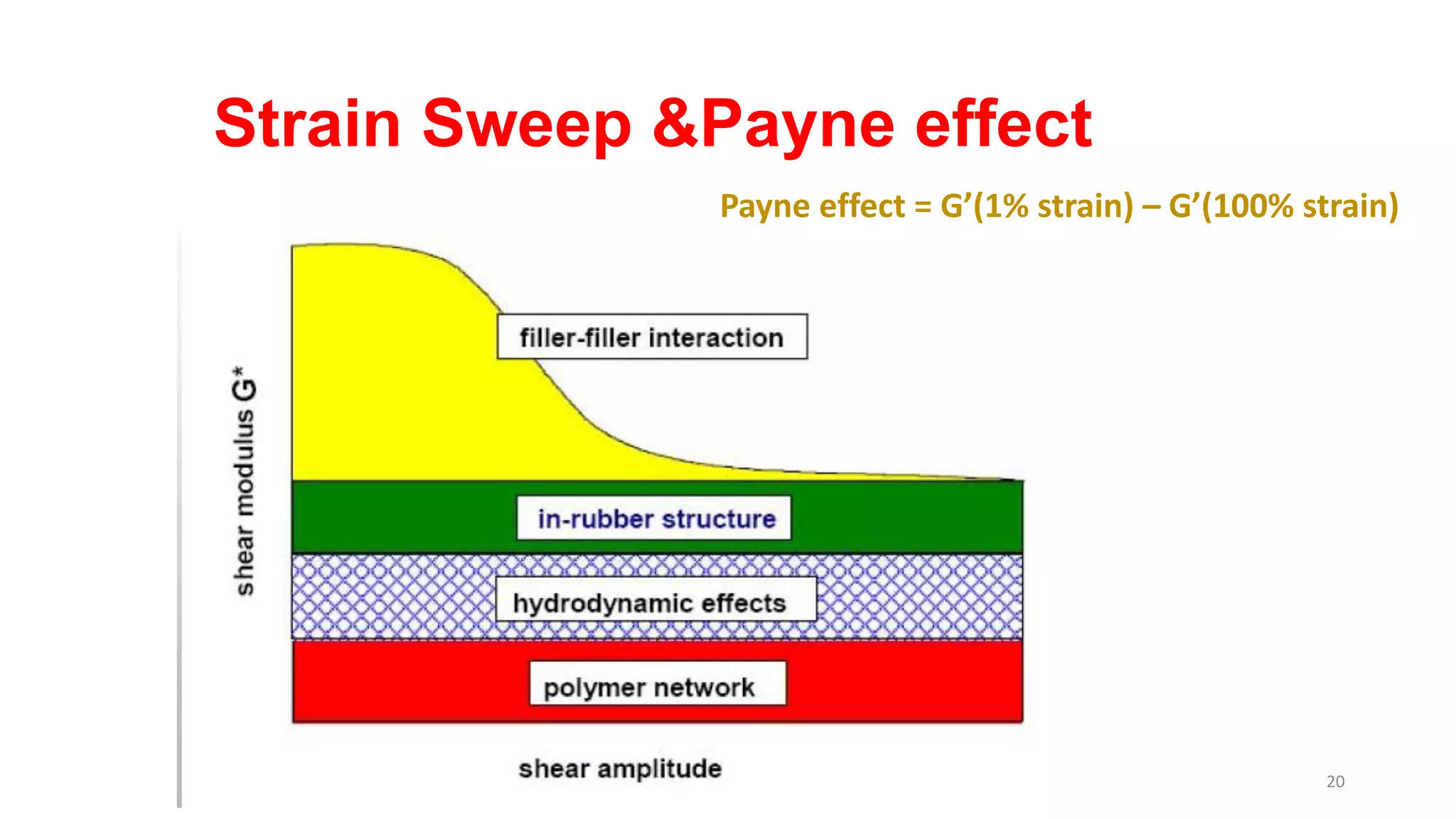
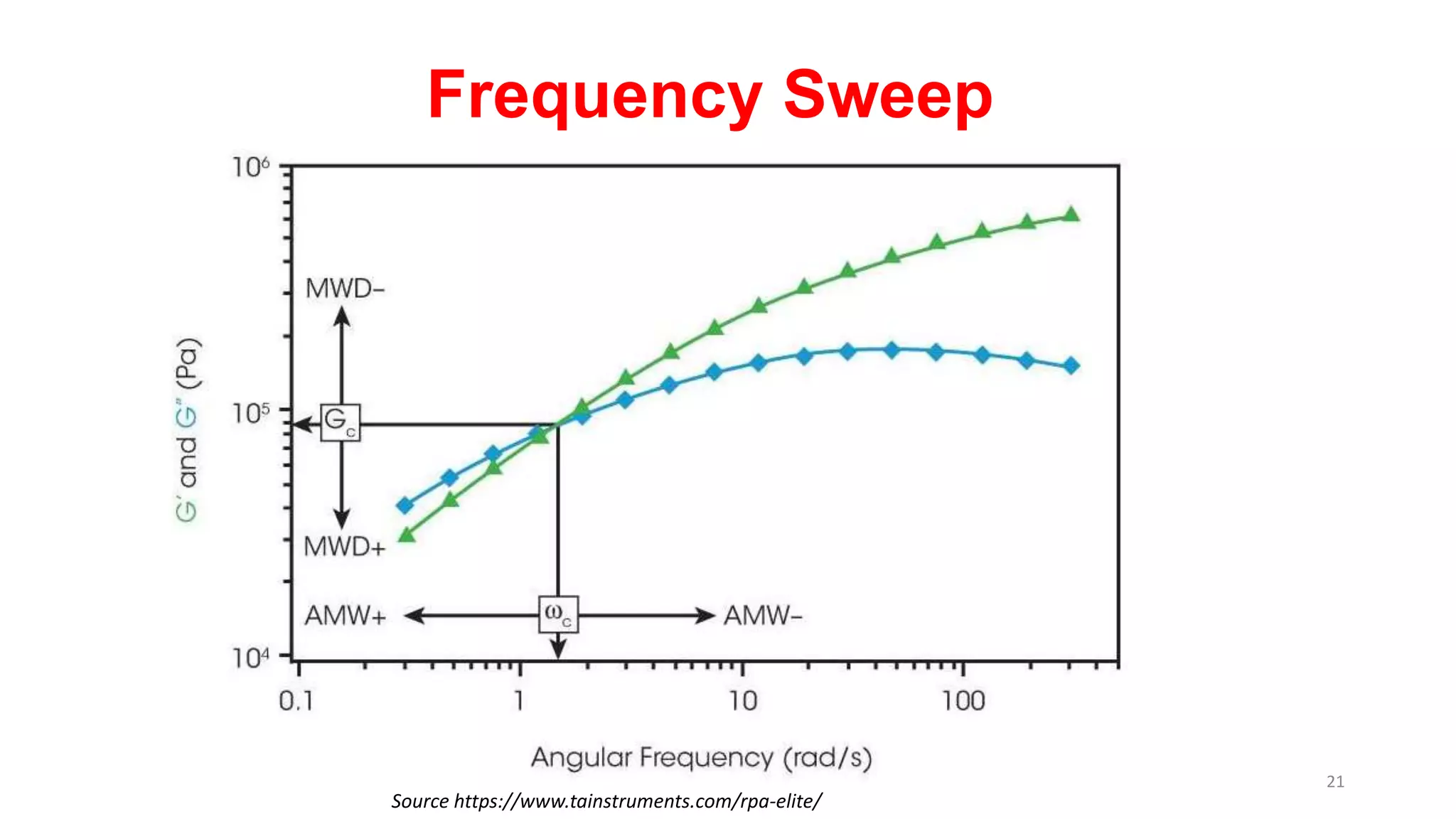
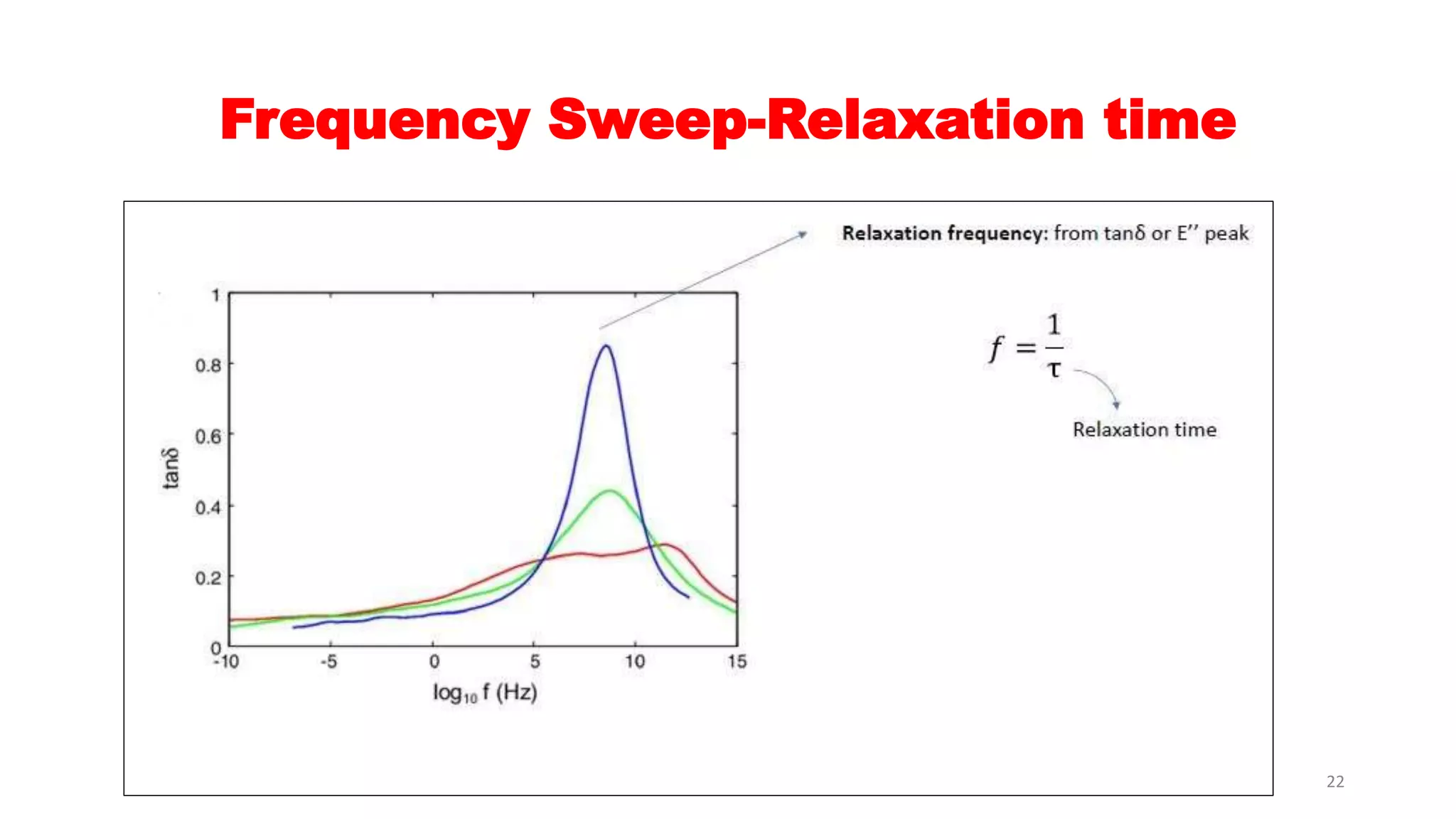
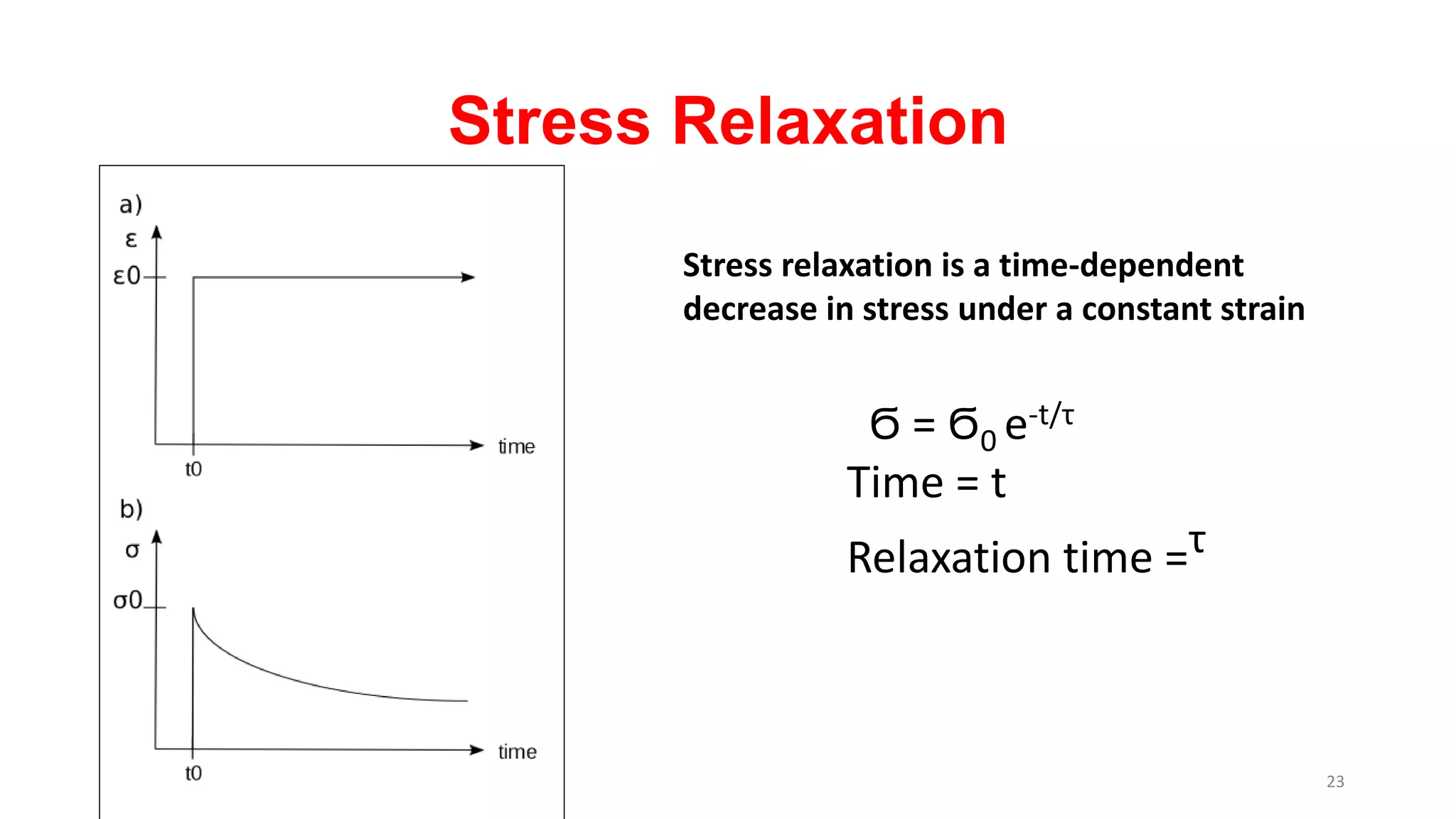
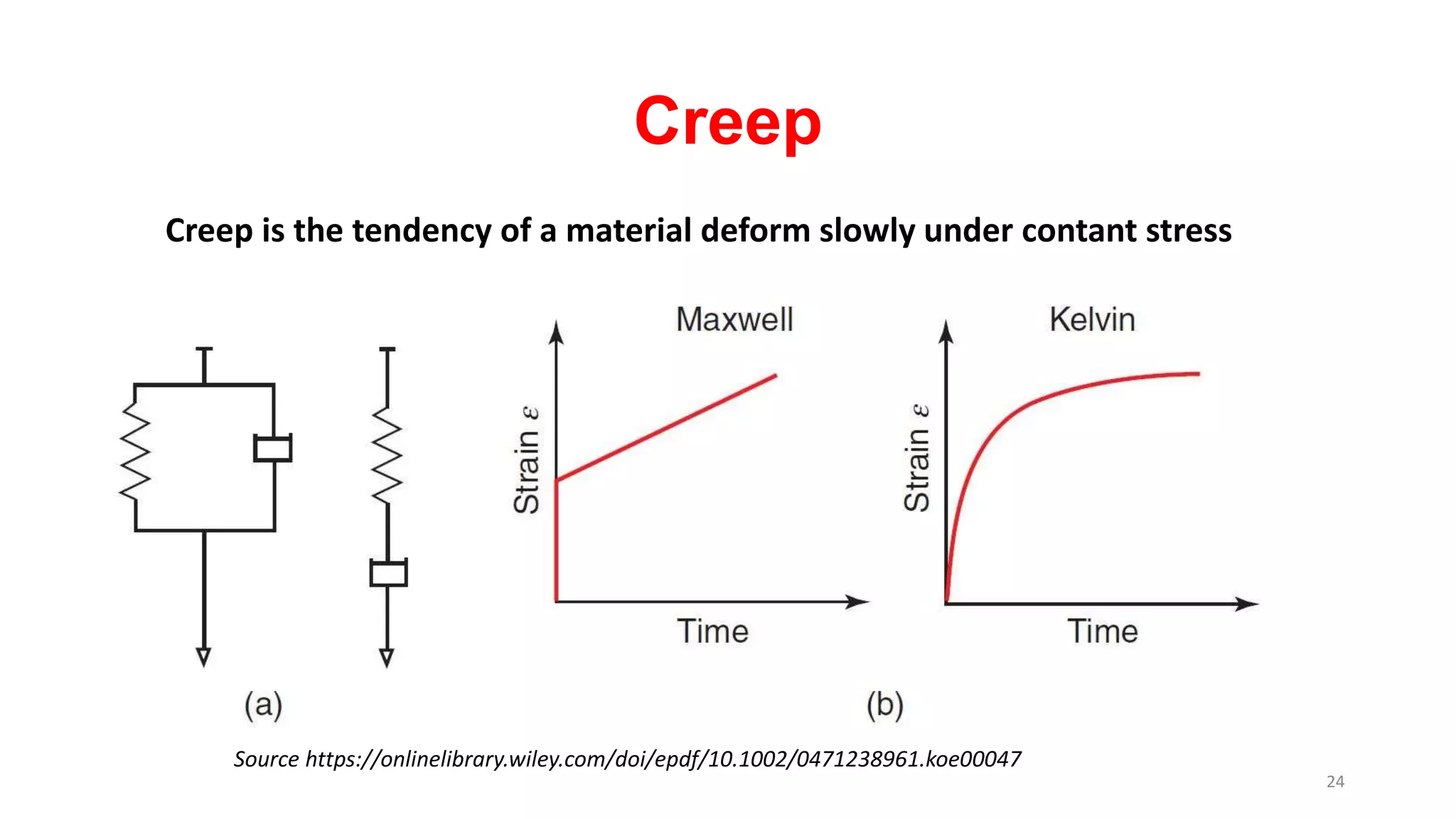
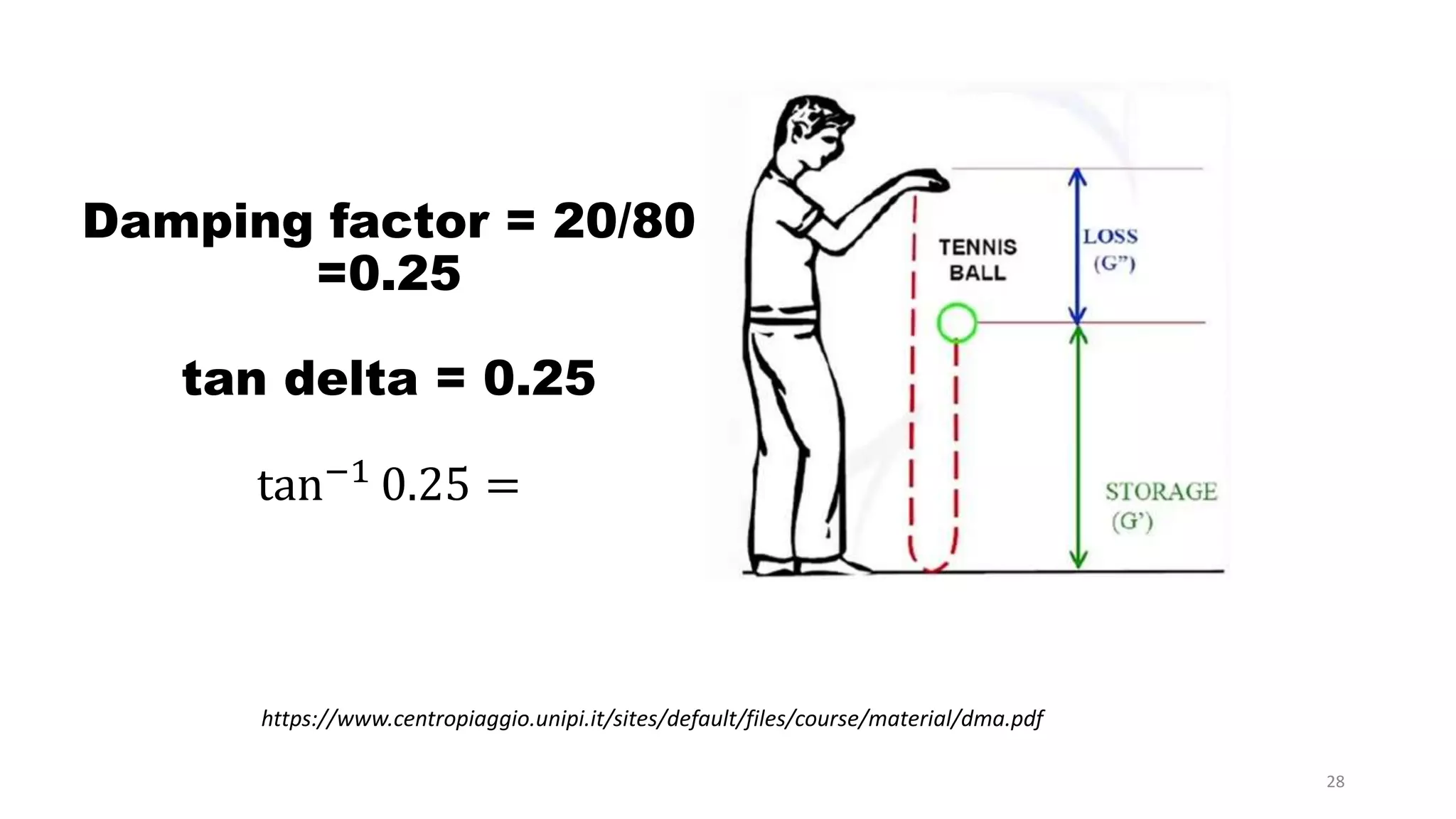
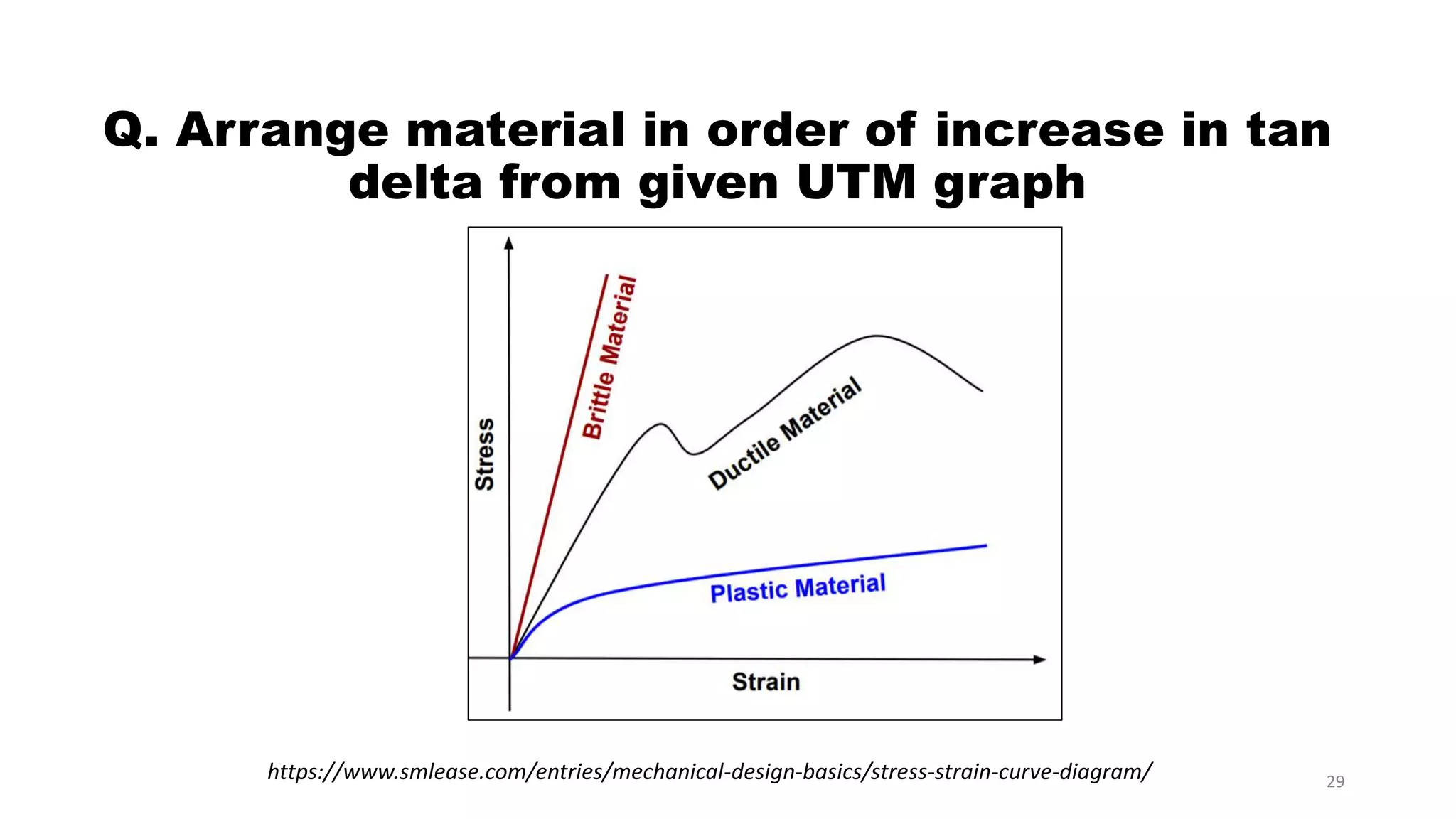
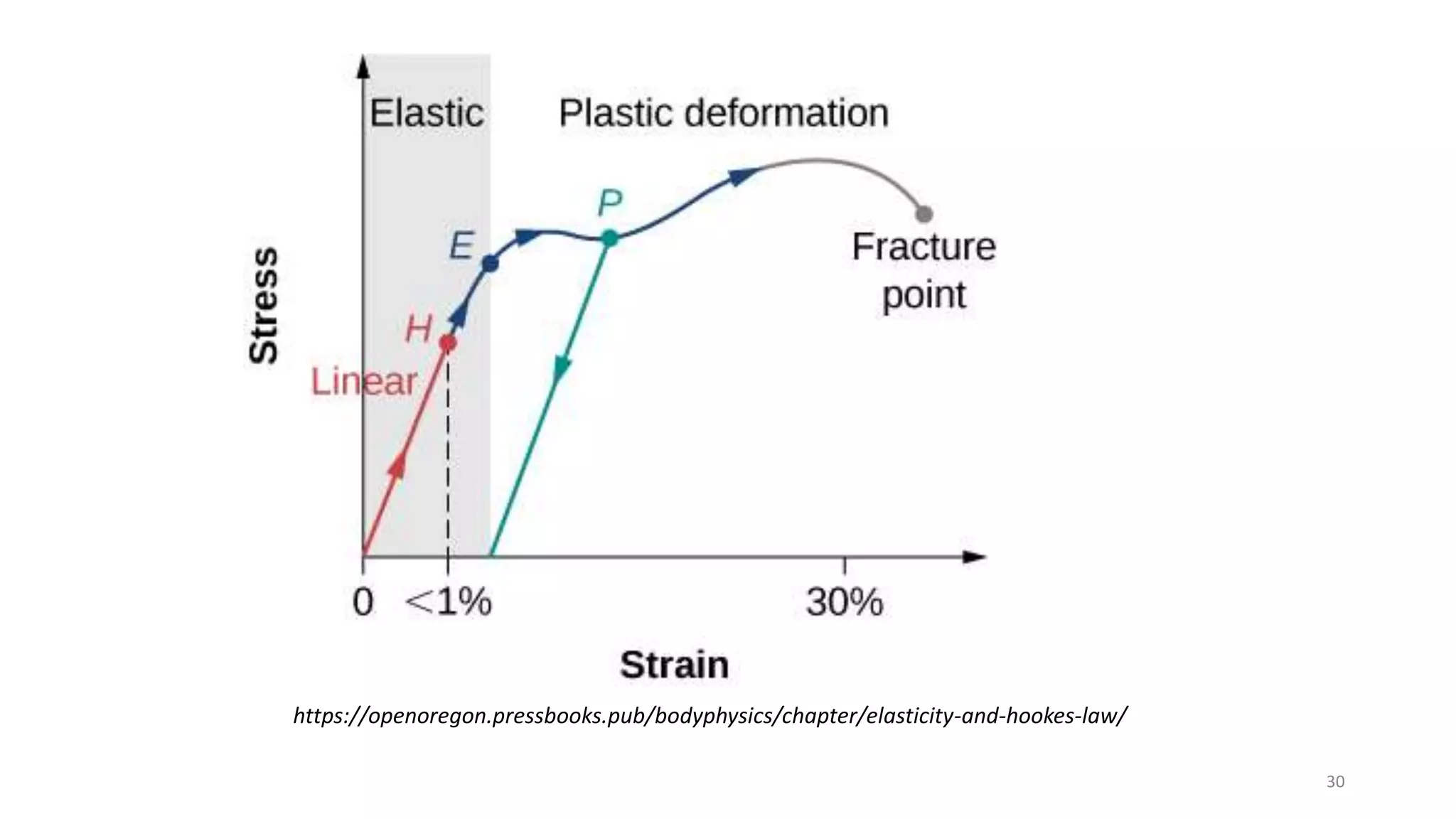
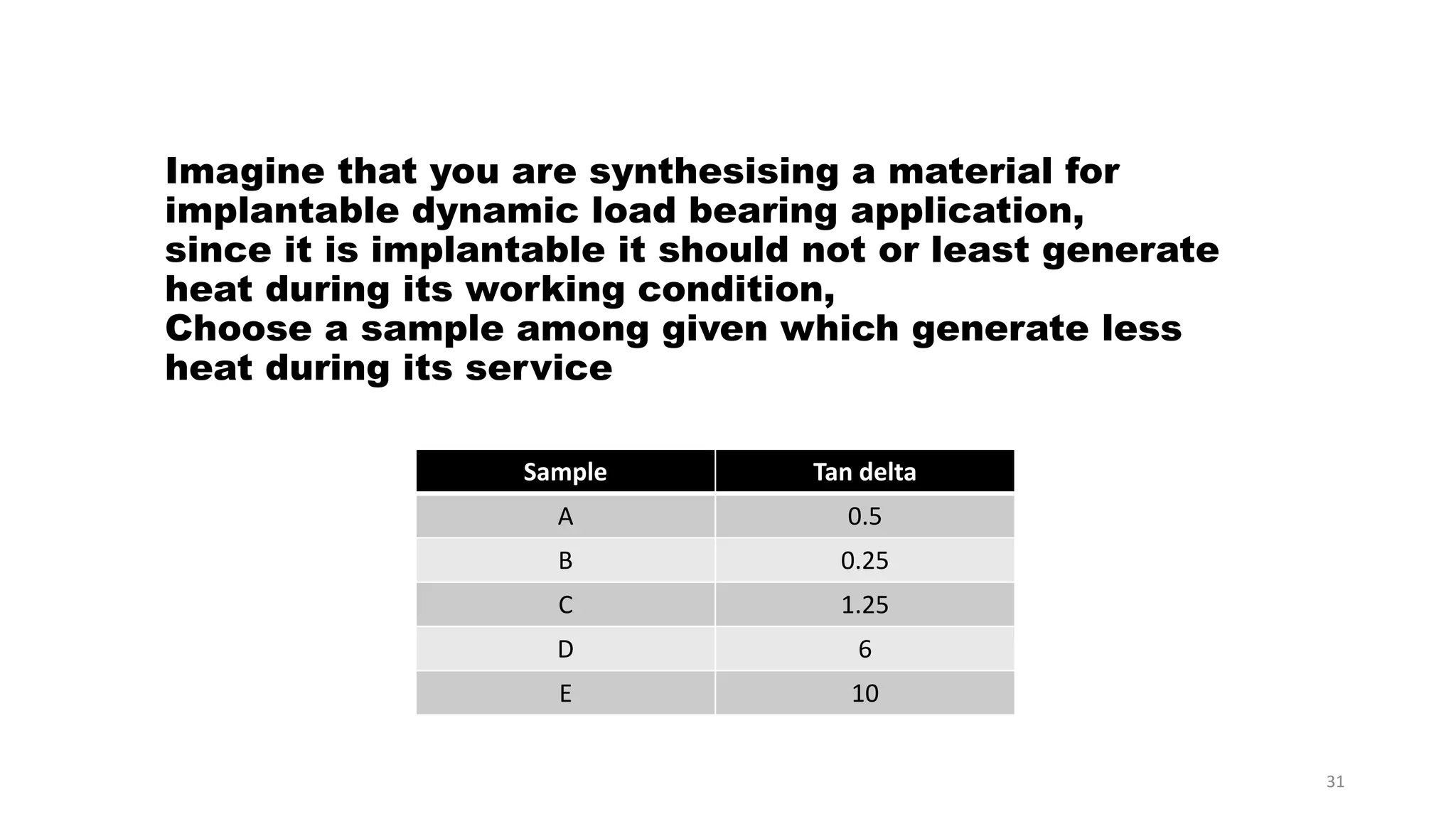
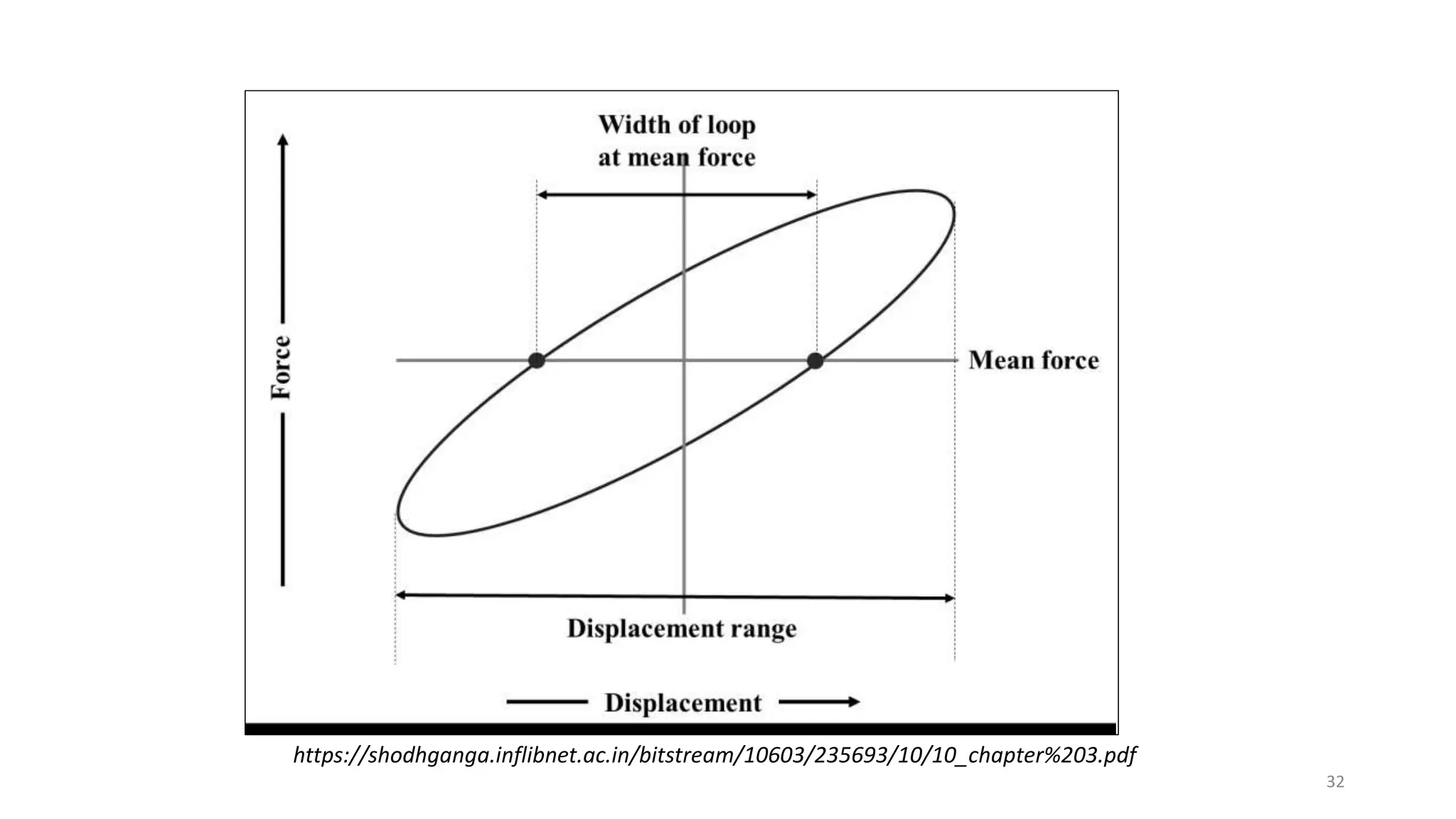
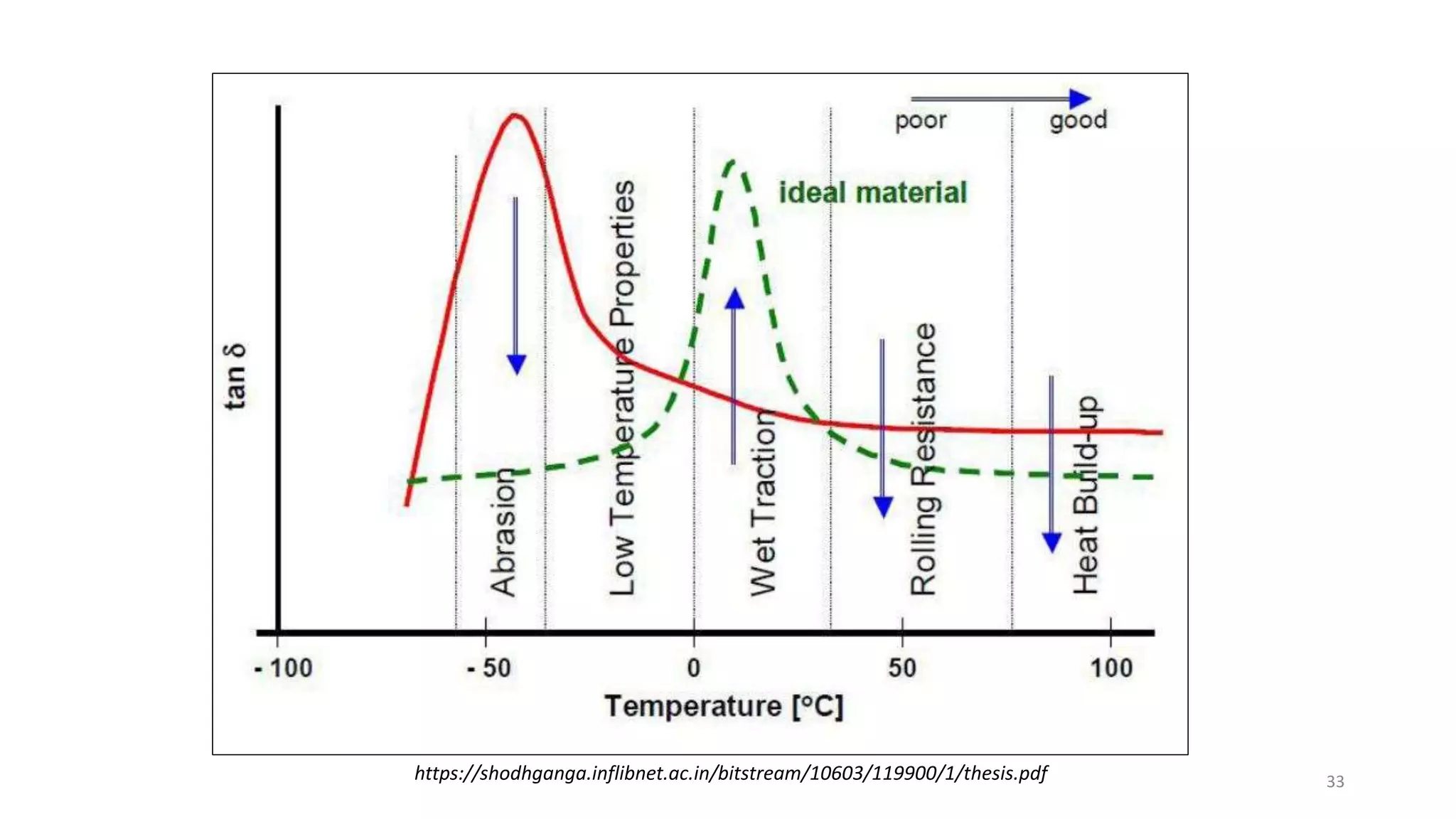
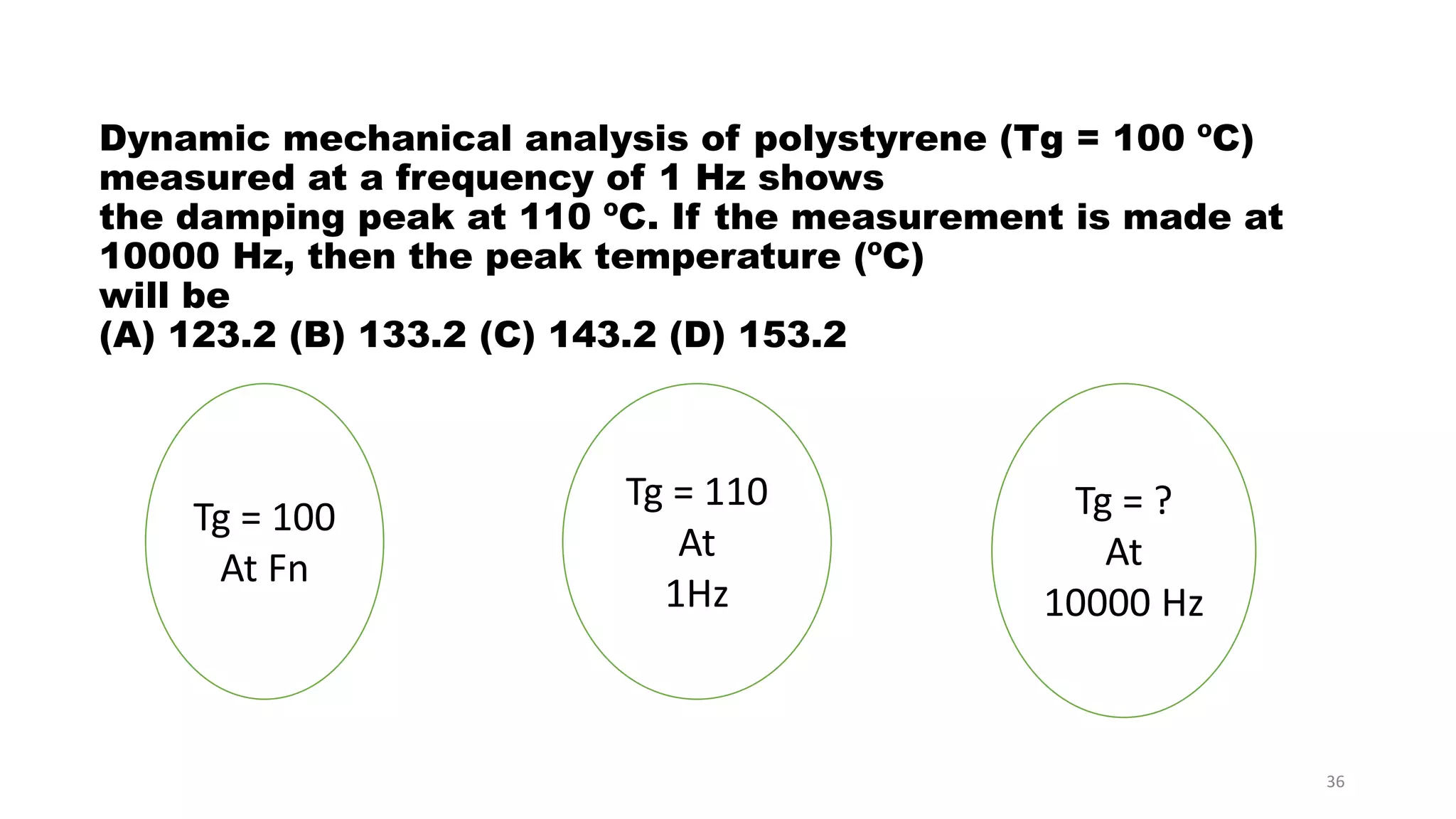
The document discusses dynamic mechanical analysis (DMA), which is used to characterize the viscoelastic properties of polymers. DMA measures properties such as storage and loss modulus under various conditions like temperature, strain, and frequency. The document outlines different DMA techniques including temperature sweeps, strain sweeps, and frequency sweeps. It also discusses viscoelastic concepts like the Maxwell and Voigt-Kelvin models, time-temperature superposition principle, stress relaxation, and creep. Finally, it provides examples of questions and calculations related to DMA measurements and viscoelastic behavior.