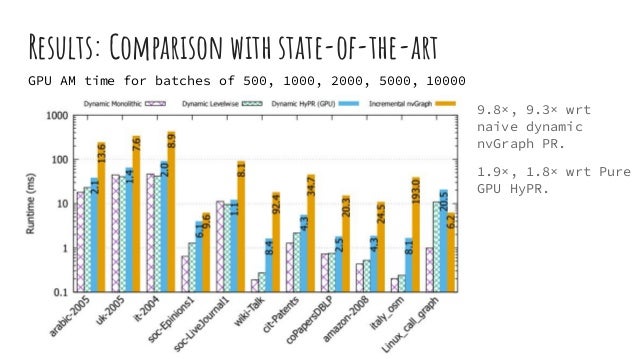
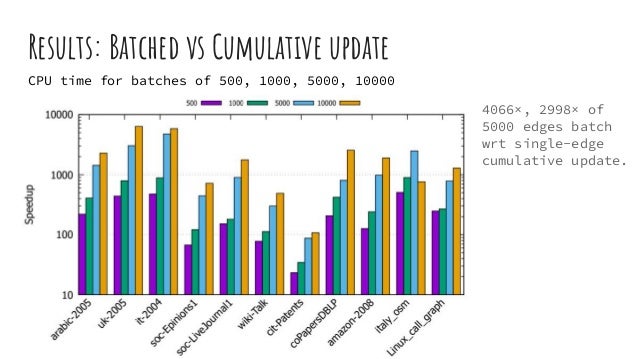
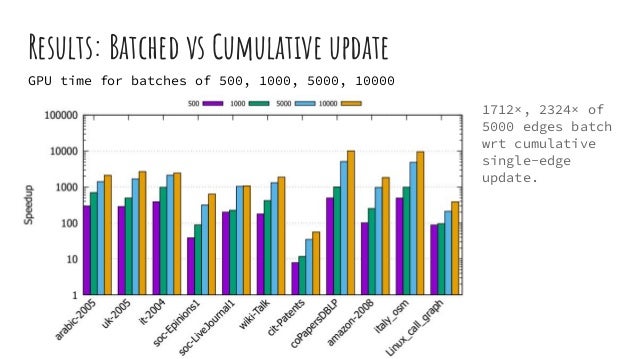
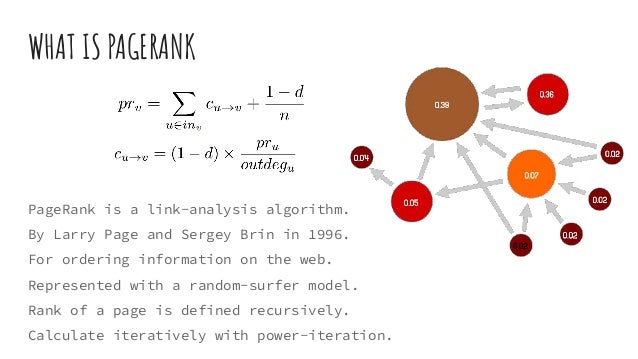
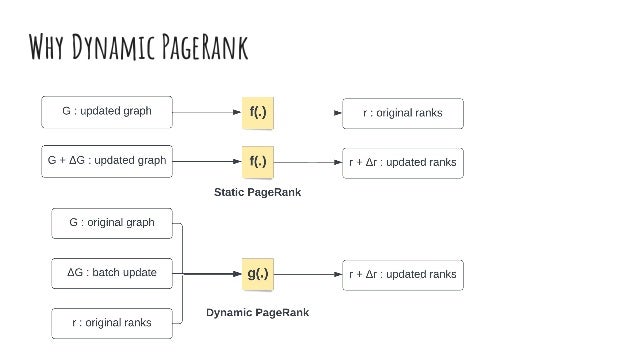
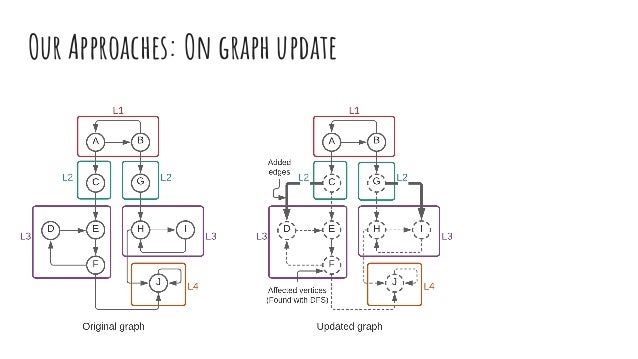
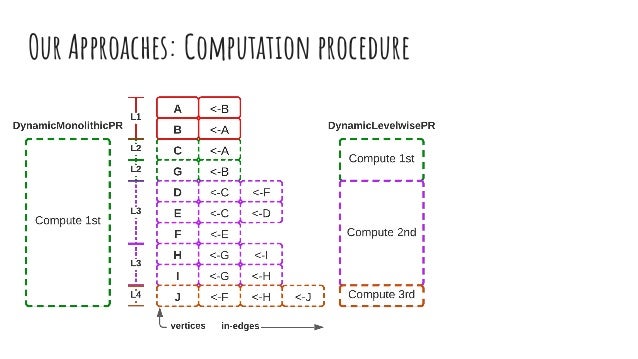
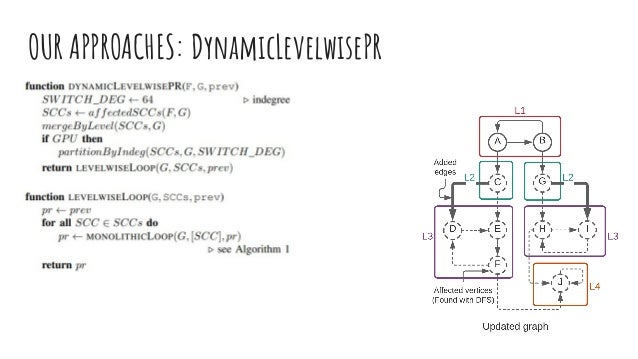
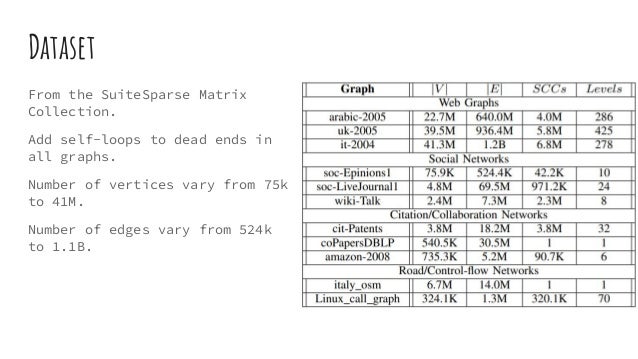
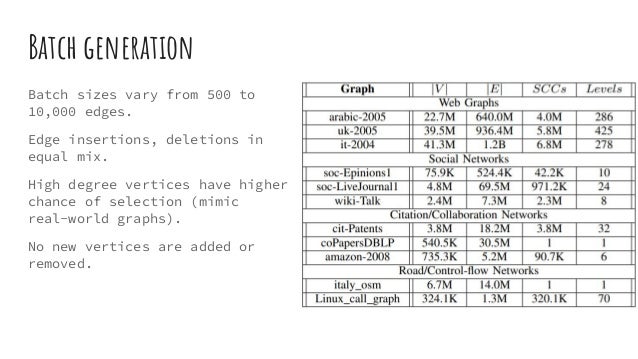
The document discusses dynamic batch parallel algorithms for updating PageRank, highlighting the importance of addressing challenges posed by large and constantly changing graphs. It compares various dynamic algorithms, including incremental, decremental, and fully dynamic types, while emphasizing the benefits of batched fully dynamic algorithms for efficiency. The research presents performance measurements on both CPU and GPU platforms, demonstrating significant improvements over existing state-of-the-art methods.

1. Dynamic Batch Parallel
Algorithms for Updating
PageRank
Subhajit Sahu†, Kishore Kothapalli† and Dip Sankar Banerjee‡
†International Institute of Information Technology Hyderabad, India.
‡Indian Institute of Technology Jodhpur, India.
subhajit.sahu@research.,kkishore@iiit.ac.in, dipsankarb@iitj.ac.in
This work is partially supported by a grant from the Department of Science and Technology (DST), India, under the
National Supercomputing Mission (NSM) R&D in Exascale initiative vide Ref. No: DST/NSM/R&D Exascale/2021/16.

2. Facebook is taking a page out
of Google’s playbook to stop
fake news from going viral
Published Apr 2019 by Salvador Rodriguez
Click-Gap: When is Facebook
is driving disproportionate
amounts of traffic to
websites.
Effort to rid fakes news
from Facebook’s services.
Is a website relying on
Facebook to drive
significant traffic, but not
well ranked by the rest of
the web?
Also News Citation Graph.

3. PAGERANK APPLICATIONS
Ranking of websites.
Measuring scientific impact of researchers.
Finding the best teams and athletes.
Ranking companies by talent concentration.
Predicting road/foot traffic in urban spaces.
Analysing protein networks.
Finding the most authoritative news sources
Identifying parts of brain that change jointly.
Toxic waste management.

4. PAGERANK APPLICATIONS
Debugging complex software systems(MonitorRank)
Finding the most original writers (BookRank)
Finding topical authorities (TwitterRank)

5. WHAT IS PAGERANK
PageRank is a link-analysis algorithm.
By Larry Page and Sergey Brin in 1996.
For ordering information on the web.
Represented with a random-surfer model.
Rank of a page is defined recursively.
Calculate iteratively with power-iteration.

6. PageRank computation approaches
Matrix multiplication.
Power-iteration (push vs pull).
Random walk (approximate).

7. Challenges & Limitations
Graphs are massive and constantly updated.
Existing dynamic algorithms do not utilize
reducibility of graphs.
Vertices which are dependent upon other vertices to
converge are still processed.
Locality benefits of SCCs are not explored.

8. Why Dynamic PageRank

9. Types of Dynamic graph algorithms
Incremental: handles 1 edge/vertex insertion.
Decremental: handles 1 edge/vertex deletion.
Fully dynamic: handles 1 insertion or deletion.
Batched fully dynamic: handles n insertions and/or
deletions.

10. Benefits of Dynamic graph algorithms
Reduces time needed for performing analytics.
Enables interactivity with dataset.
Batched fully dynamic algorithms accept a batch of
updates to minimize computation needed in contrast
to single-update fully dynamic ones.

11. Our Approaches: On graph update

12. Our Approaches: Computation procedure

13. Our Approaches: GPU-specific optimization

14. OUR APPROACHES: DynamicMonolithicPR
Full power-iteration, process all vertices.
Group vertices by SCC for better access.
Partition vertices by in-degree on GPU.
Use old ranks, skip unaffected vertices.
Affected vertices found with DFS.
Faster on GPU with CUDA.

15. OUR APPROACHES: DynamicMonolithicPR

16. OUR APPROACHES: DynamicLevelwisePR
Contrast to full power-iteration.
Process vertices in levels of SCCs.
Avoid converged/unstable vertices.
No per-iteration sharing of ranks.
Faster on CPU with OpenMP.
Slightly higher error.
Requires graph to be dead-end free.

17. OUR APPROACHES: DynamicLevelwisePR

18. Dataset
From the SuiteSparse Matrix
Collection.
Add self-loops to dead ends in
all graphs.
Number of vertices vary from 75k
to 41M.
Number of edges vary from 524k
to 1.1B.

19. Batch generation
Batch sizes vary from 500 to
10,000 edges.
Edge insertions, deletions in
equal mix.
High degree vertices have higher
chance of selection (mimic
real-world graphs).
No new vertices are added or
removed.

20. Platform
Intel(R) Xeon(R) Silver 4116 CPU (12 cores) x 2; Cache L1:
768KB, L2: 12MB, L3: 16MB (shared).
NVIDIA Tesla V100 GPU (16GB PCIe); 14 TFLOPs SP (84 SMs x 64
FP/INT cores), 16GB 900GB/s HBM2 DRAM, 32 GB/s PCIe.
CentOS 7.9, OpenMP 5.0, CUDA 11.3, GCC 9.3.

21. Performance measurement
Damping factor d of 0.15.
Tolerance τ of 10−6.
Maximum of 500 iterations.
32-bit integers for CSR representation.
32-bit floats for rank vector.
L∞-norm for error measurement,
(L2-norm for nvGraph PageRank).
Measured time only rank computation.

22. Results: Comparison with state-of-the-art
CPU AM time for batches of 500, 1000, 2000, 5000, 10000
6.1×, 8.6× wrt
static plain STIC-D
PR [1].
4.2×, 5.8× wrt Pure
CPU HyPR [2].

23. Results: Comparison with state-of-the-art
GPU AM time for batches of 500, 1000, 2000, 5000, 10000
9.8×, 9.3× wrt
naive dynamic
nvGraph PR.
1.9×, 1.8× wrt Pure
GPU HyPR.

24. Results: Batched vs Cumulative update
CPU time for batches of 500, 1000, 5000, 10000
4066×, 2998× of
5000 edges batch
wrt single-edge
cumulative update.

25. Results: Batched vs Cumulative update
GPU time for batches of 500, 1000, 5000, 10000
1712×, 2324× of
5000 edges batch
wrt cumulative
single-edge
update.

26. Conclusion
DynamicLevelwisePR is a suitable approach on CPU.
On a GPU, smaller levels should be combined and processed at a time.
On 1 SCC graphs, both algorithms perform ~identically.