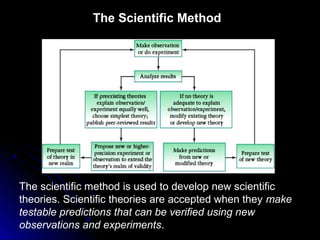
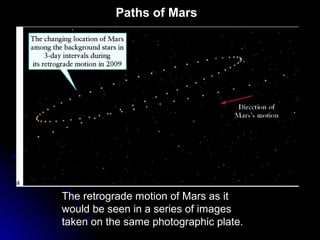
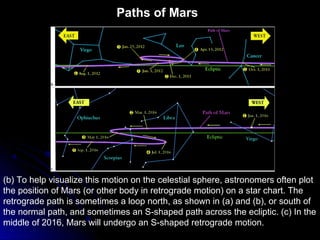
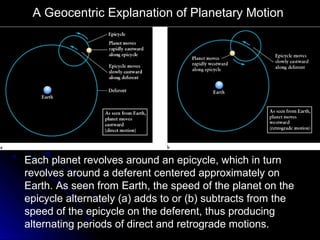
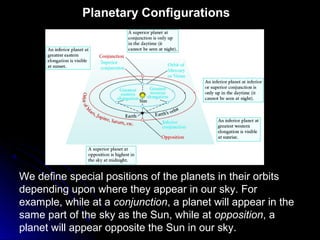
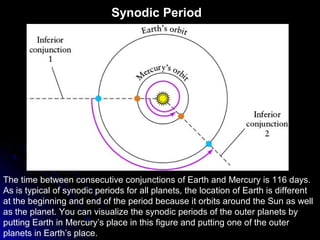
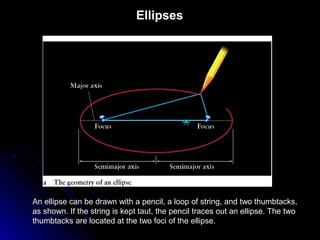
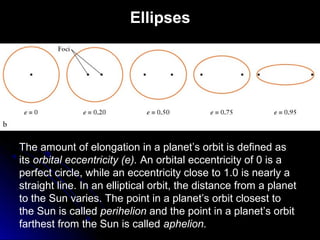
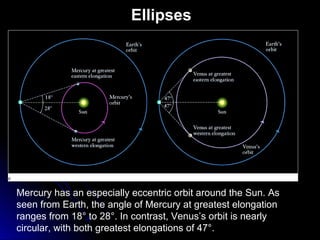
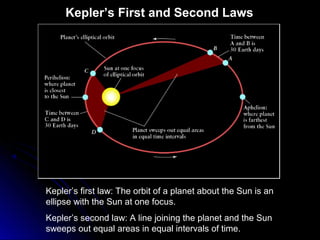
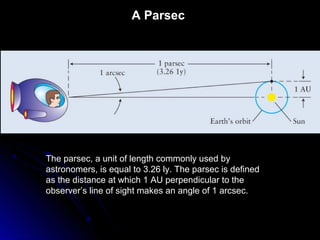
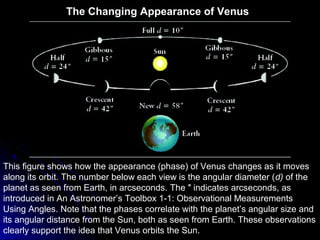
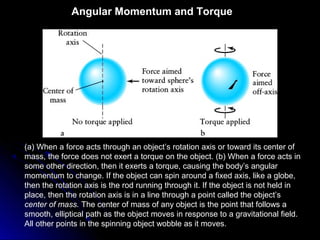
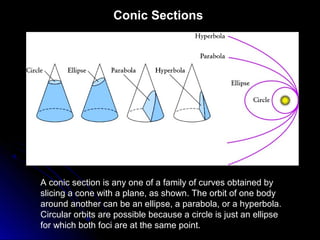
This chapter discusses the scientific discoveries that revealed the Earth is not at the center of the universe, including Copernicus's argument that planets orbit the Sun. It describes how Kepler determined planetary orbits depend on Tycho Brahe's observations, and how Newton formulated the law of gravity to explain why planets remain in orbit. The scientific method is used to develop theories through observation, hypothesis, prediction, testing, modification and simplification.

2. In this chapter you will discover…In this chapter you will discover…
 what makes a theory scientificwhat makes a theory scientific
 the scientific discoveries that revealed that Earth is not atthe scientific discoveries that revealed that Earth is not at
the center of the universe, as previously believedthe center of the universe, as previously believed
 Copernicus’s argument that the planets orbit the SunCopernicus’s argument that the planets orbit the Sun
 why the direction of motion of each planet on thewhy the direction of motion of each planet on the
celestial sphere sometimes changescelestial sphere sometimes changes
 that Kepler’s determination of the shapes and otherthat Kepler’s determination of the shapes and other
properties of planetary orbits depended on the carefulproperties of planetary orbits depended on the careful
observations of his mentor Tycho Braheobservations of his mentor Tycho Brahe
 how Isaac Newton formulated an equation to describehow Isaac Newton formulated an equation to describe
the force of gravity and how he thereby explained whythe force of gravity and how he thereby explained why
the planets and moons remain in orbitthe planets and moons remain in orbit

3. The scientific method is used to develop new scientific
theories. Scientific theories are accepted when they make
testable predictions that can be verified using new
observations and experiments.
The Scientific Method

4. Science is both a body of knowledge and a
process of learning about nature
 The scientific method is a process by which scientistsThe scientific method is a process by which scientists
study nature and develop new scientific theories.study nature and develop new scientific theories.
 A scientific theory must be testable, that is, capable ofA scientific theory must be testable, that is, capable of
being disproved.being disproved.
 Theories are tested and verified by observation orTheories are tested and verified by observation or
experimentation and result in a process that often leadsexperimentation and result in a process that often leads
to their refinement or replacement and to the progressto their refinement or replacement and to the progress
of science.of science.
 Observations of the cosmos have led astronomers toObservations of the cosmos have led astronomers to
discover some fundamental physical laws of thediscover some fundamental physical laws of the
universe.universe.
 The scientific method can be summarized by theThe scientific method can be summarized by the
following words: observe, hypothesize, predict, test,following words: observe, hypothesize, predict, test,
modify, and simplifymodify, and simplify

5. The retrograde motion of Mars as it
would be seen in a series of images
taken on the same photographic plate.
Paths of Mars

6. (b) To help visualize this motion on the celestial sphere, astronomers often plot
the position of Mars (or other body in retrograde motion) on a star chart. The
retrograde path is sometimes a loop north, as shown in (a) and (b), or south of
the normal path, and sometimes an S-shaped path across the ecliptic. (c) In the
middle of 2016, Mars will undergo an S-shaped retrograde motion.
Paths of Mars

7. Each planet revolves around an epicycle, which in turn
revolves around a deferent centered approximately on
Earth. As seen from Earth, the speed of the planet on the
epicycle alternately (a) adds to or (b) subtracts from the
speed of the epicycle on the deferent, thus producing
alternating periods of direct and retrograde motions.
A Geocentric Explanation of Planetary Motion

8. Ptolemy and Retrograde MotionPtolemy and Retrograde Motion
 The geocentric (Earth-centered) solar system modelThe geocentric (Earth-centered) solar system model
emerged because one could not feel the Earth moveemerged because one could not feel the Earth move
under them, and objects in the sky appeared to moveunder them, and objects in the sky appeared to move
past the observer.past the observer.
 Ptolemy explained retrograde motion using epicyclesPtolemy explained retrograde motion using epicycles
around a larger circle (deferent) with unprecedentedaround a larger circle (deferent) with unprecedented
accuracy. Eventually, adjustments had to be made andaccuracy. Eventually, adjustments had to be made and
astronomers realized they needed a new theory.astronomers realized they needed a new theory.

9. Earth travels around the Sun more rapidly than does
Mars. Consequently, as Earth overtakes and passes this
slower-moving planet, Mars appears (from points 4
through 6) to move backward among the background stars
for a few months.
A Heliocentric Explanation of Retrograde Motion

10. Nicolaus Copernicus (1473–1543)
Copernicus, the youngest of four
children, was born in Torun, Poland.
He pursued his higher education in
Italy, where he received a doctorate
in canon law and studied medicine.
Copernicus developed a
heliocentric theory of the known
universe and just before his death
in 1543 published this work under
the title De Revolutionibus Orbium
Coelestium. His revolutionary theory
was flawed in that he assumed that
the planets had circular orbits
around the Sun. This was corrected
by Johannes Kepler.

11. Tycho Brahe (1546–1601)
Tycho (depicted to the right and
within the portrait of Kepler) was born
to nobility in the Danish city of
Knudstrup, which is now part of
Sweden. At age 20, he lost part of his
nose in a duel and wore a metal
replacement thereafter. In 1576, the
Danish king Frederick II built Tycho
an astronomical observatory that
Tycho named Uraniborg (after
Urania, Greek muse of astronomy).
Tycho rejected both Copernicus’s
heliocentric theory and the Ptolemaic
geocentric system. He devised a
halfway theory called the Tychonic
system. According to Tycho’s theory,
Earth is stationary, with the Sun and
the Moon revolving around it, while
all the other planets revolve around
the Sun.

12. Kepler was educated in
Germany, where he spent 3
years studying mathematics,
philosophy, and theology. In
1596, Kepler published a
booklet in which he attempted
to mathematically predict the
planetary orbits. Although his
theory was altogether wrong,
its boldness and originality
attracted the attention of
Tycho Brahe, whose staff
Kepler joined in 1600. Kepler
deduced his three laws from
Tycho’s observations.
Johannes Kepler (1571–1630)

13. Galileo Galilei (1564–1642)
Born in Pisa, Italy, Galileo studied
medicine and philosophy at the University
of Pisa. He abandoned medicine in favor
of mathematics. He held the chair of
mathematics at the University of Padua,
and eventually returned to the University
of Pisa as a professor of mathematics.
There Galileo formulated his famous law
of falling bodies: All objects fall with the
same acceleration regardless of their
weight. In 1609 he constructed a
telescope and made a host of discoveries
that contradicted the teachings of Aristotle
and the Roman Catholic Church. He
summed up his life’s work on motion,
acceleration, and gravity in the book
Dialogues Concerning the Two Chief
World Systems, published in 1632.

14. Isaac Newton (1642–1727)
Newton delighted in constructing mechanical
devices, such as sundials, model windmills, a
water clock, and a mechanical carriage. He
received a bachelor’s degree in 1665 from
the University of Cambridge. While there, he
began developing the mathematics that later
became calculus (developed independently
by the German philosopher and
mathematician Gottfried Leibniz, 1646–
1716). While pursuing experiments in optics,
Newton constructed a reflecting telescope
and also discovered that white light is actually
a mixture of all colors. His major work on
forces and gravitation was the tome
Philosophiae Naturalis Principia
Mathematica, which appeared in 1687. In
1704, Newton published his second great
treatise, Opticks, in which he described his
experiments and theories about light and
color. Upon his death in 1727, Newton was
buried in Westminster Abbey, the first
scientist to be so honored.

15. We define special positions of the planets in their orbits
depending upon where they appear in our sky. For
example, while at a conjunction, a planet will appear in the
same part of the sky as the Sun, while at opposition, a
planet will appear opposite the Sun in our sky.
Planetary Configurations

16. Synodic Period
The time between consecutive conjunctions of Earth and Mercury is 116 days.
As is typical of synodic periods for all planets, the location of Earth is different
at the beginning and end of the period because it orbits around the Sun as well
as the planet. You can visualize the synodic periods of the outer planets by
putting Earth in Mercury’s place in this figure and putting one of the outer
planets in Earth’s place.

17. Parallax
Nearby objects are viewed
at different angles from
different places, an effect
called parallax. These
objects also appear to be
in different places with
respect to more distant
objects when viewed by
observers located at
different positions.
Parallax is used by
astronomers, surveyors,
and sailors to determine
distances.

18. Tycho thought that Earth does not
rotate and that the stars revolve
around it. From our modern
perspective, the changing position of
the supernova would be due to Earth’s
rotation as shown. (a) Tycho argued
that if an object is near Earth, its
position relative to the background
stars should change over the course of
a night. (b) Tycho failed to measure
such changes for the supernova in
1572. This is illustrated in (b) by the
two telescopes being parallel to each
other. He therefore concluded that the
object was far from Earth.
The Parallax of a Nearby Object in Space

19. An ellipse can be drawn with a pencil, a loop of string, and two thumbtacks,
as shown. If the string is kept taut, the pencil traces out an ellipse. The two
thumbtacks are located at the two foci of the ellipse.
Ellipses

20. The amount of elongation in a planet’s orbit is defined as
its orbital eccentricity (e). An orbital eccentricity of 0 is a
perfect circle, while an eccentricity close to 1.0 is nearly a
straight line. In an elliptical orbit, the distance from a planet
to the Sun varies. The point in a planet’s orbit closest to
the Sun is called perihelion and the point in a planet’s orbit
farthest from the Sun is called aphelion.
Ellipses

21. Mercury has an especially eccentric orbit around the Sun. As
seen from Earth, the angle of Mercury at greatest elongation
ranges from 18° to 28°. In contrast, Venus’s orbit is nearly
circular, with both greatest elongations of 47°.
Ellipses

22. Kepler’s first law: The orbit of a planet about the Sun is an
ellipse with the Sun at one focus.
Kepler’s second law: A line joining the planet and the Sun
sweeps out equal areas in equal intervals of time.
Kepler’s First and Second Laws

23. Kepler’s Third LawKepler’s Third Law
 The square of a planet’s sidereal periodThe square of a planet’s sidereal period
around the Sun is directly proportional toaround the Sun is directly proportional to
the cube of the length of its orbit’sthe cube of the length of its orbit’s
semimajor axis.semimajor axis.
PP22
== aa33
 This equation says that a planet closer toThis equation says that a planet closer to
the Sun has a shorter year than does athe Sun has a shorter year than does a
planet farther from the Sun. In other wordsplanet farther from the Sun. In other words
planets closer to the Sun move moreplanets closer to the Sun move more
rapidly than those farther away.rapidly than those farther away.

25. Units of Astronomical DistanceUnits of Astronomical Distance
 Astronomical Unit (AU) is the averageAstronomical Unit (AU) is the average
distance from Earth to the Sun, about 1.5distance from Earth to the Sun, about 1.5
x 10x 1088
km (9.3 x 10km (9.3 x 1077
mi).mi).
 Light year (ly) is the distance light travelsLight year (ly) is the distance light travels
in one year through a vacuum: 9.46 x 10in one year through a vacuum: 9.46 x 101212
km or 63,200 AU.km or 63,200 AU.
 Parsec as shown in the following diagram:Parsec as shown in the following diagram:
3.09 x 103.09 x 101313
km or 3.26 ly.km or 3.26 ly.

26. The parsec, a unit of length commonly used by
astronomers, is equal to 3.26 ly. The parsec is defined
as the distance at which 1 AU perpendicular to the
observer’s line of sight makes an angle of 1 arcsec.
A Parsec

27. This figure shows how the appearance (phase) of Venus changes as it moves
along its orbit. The number below each view is the angular diameter (d) of the
planet as seen from Earth, in arcseconds. The ″ indicates arcseconds, as
introduced in An Astronomer’s Toolbox 1-1: Observational Measurements
Using Angles. Note that the phases correlate with the planet’s angular size and
its angular distance from the Sun, both as seen from Earth. These observations
clearly support the idea that Venus orbits the Sun.
The Changing Appearance of Venus

28. In 1610, Galileo discovered
four “stars” that move back
and forth across Jupiter. He
concluded that they are four
moons that orbit Jupiter just
as our Moon orbits Earth.
The observations shown
were made by Jesuits in
1620 of Jupiter and its four
visible moons.
Jupiter and Its Largest Moons

29. This is a photograph of the four Galilean satellites alongside an
overexposed image of Jupiter. Each satellite would be bright
enough to be seen with the unaided eye were it not
overwhelmed by the glare of Jupiter.
Jupiter and Its Largest Moons

30. Newton’s Three Laws of Motion
 Newton’s First Law—The Law of Inertia:Newton’s First Law—The Law of Inertia: Inertia is theInertia is the
property of matter that keeps an object at rest or movingproperty of matter that keeps an object at rest or moving
in a straight line at a constant speed unless acted on byin a straight line at a constant speed unless acted on by
a net external force.a net external force.
 Newton’s Second Law—The Force Law:Newton’s Second Law—The Force Law: TheThe
acceleration of an object is directly proportional to theacceleration of an object is directly proportional to the
net force acting on it and is inversely proportional to itsnet force acting on it and is inversely proportional to its
mass.mass.
 Newton’s Third Law—The Law of Action andNewton’s Third Law—The Law of Action and
Reaction:Reaction: Whenever one object exerts a force on aWhenever one object exerts a force on a
second object, the second object exerts an equal andsecond object, the second object exerts an equal and
opposite force on the first object.opposite force on the first object.

31. As this skater brings her arms and outstretched leg in,
she must spin faster to conserve her angular momentum.
Conservation of Angular Momentum

32. Terms to RememberTerms to Remember
 Velocity includes speed and direction while accelerationVelocity includes speed and direction while acceleration
is a change in velocity.is a change in velocity.
 Mass is the amount of matter in a substance, whereasMass is the amount of matter in a substance, whereas
weight is a measurement of a force like gravity.weight is a measurement of a force like gravity.
 Kinetic energy is associated with an object’s motion.Kinetic energy is associated with an object’s motion.
 Potential energy is the energy stored in an object usuallyPotential energy is the energy stored in an object usually
by its location.by its location.

33. (a) When a force acts through an object’s rotation axis or toward its center of
mass, the force does not exert a torque on the object. (b) When a force acts in
some other direction, then it exerts a torque, causing the body’s angular
momentum to change. If the object can spin around a fixed axis, like a globe,
then the rotation axis is the rod running through it. If the object is not held in
place, then the rotation axis is in a line through a point called the object’s
center of mass. The center of mass of any object is the point that follows a
smooth, elliptical path as the object moves in response to a gravitational field.
All other points in the spinning object wobble as it moves.
Angular Momentum and Torque

34. Newton’s Law of Gravitation
 G is a constant showing the strength of gravity; m1 and
m2 are masses; and r is the distance between the centers
of the objects.
 Using the law of gravitation, Newton was able to derive
Kepler’s laws of motion.
1 2
2
Gm m
F
r
= 1 2
2
Gm m
F
r
= 1 2
2
Gm m
F
r
= 1 2
2
Gm m
F
r
=
1 2
2
Gm m
F
r
=

35. A conic section is any one of a family of curves obtained by
slicing a cone with a plane, as shown. The orbit of one body
around another can be an ellipse, a parabola, or a hyperbola.
Circular orbits are possible because a circle is just an ellipse
for which both foci are at the same point.
Conic Sections

36. Halley’s Comet orbits the Sun with an average period of about 76 years. During
the twentieth century, the comet passed near the Sun twice—once in 1910 and
again, as shown here, in 1986. The comet will pass close to the Sun again in
2061. During its last visit, the comet spread more than 5° across the sky, or 10
times the diameter of the Moon.
Halley’s Comet

37. This figure shows a few of
the effects of gravity here
on Earth, in the solar
system, in our Milky Way
Galaxy, and beyond. The
arrow in the cluster of
galaxies shows the
direction of the force of
gravity from one cluster
(bright group of galaxies
on the right) on another
cluster of galaxies.
Gravity Works at All Scales

38. Summary of Key IdeasSummary of Key Ideas

39. Science: Key to Comprehending the Cosmos
 The ancient Greeks laid the groundwork for progress inThe ancient Greeks laid the groundwork for progress in
science by stating that the universe is comprehensible.science by stating that the universe is comprehensible.
 The scientific method is a procedure for formulatingThe scientific method is a procedure for formulating
theories that correctly predict how the universe behaves.theories that correctly predict how the universe behaves.
 A scientific theory must be testable, that is, capable ofA scientific theory must be testable, that is, capable of
being disproved.being disproved.
 Theories are tested and verified by observation orTheories are tested and verified by observation or
experimentation and result in a process that often leadsexperimentation and result in a process that often leads
to their refinement or replacement and to the progress ofto their refinement or replacement and to the progress of
science.science.
 Observations of the cosmos have led astronomers toObservations of the cosmos have led astronomers to
discover some fundamental physical laws of thediscover some fundamental physical laws of the
universe.universe.

40. Origins of a Sun-centered Universe
 Common sense (e.g., Earth doesn’t appear to be moving) ledCommon sense (e.g., Earth doesn’t appear to be moving) led
early natural philosophers to devise a geocentric cosmology,early natural philosophers to devise a geocentric cosmology,
which placed Earth at the center of the universe.which placed Earth at the center of the universe.
 Kepler modified Copernicus’s heliocentric (Sun-centered)Kepler modified Copernicus’s heliocentric (Sun-centered)
theory by showing that orbits are elliptical, thereby creating atheory by showing that orbits are elliptical, thereby creating a
simplified explanation of planetary motions compared to thesimplified explanation of planetary motions compared to the
geocentric theory.geocentric theory.
 The heliocentric cosmology refers to motion of planets andThe heliocentric cosmology refers to motion of planets and
smaller debris orbiting the Sun. Other stars do not orbit thesmaller debris orbiting the Sun. Other stars do not orbit the
Sun.Sun.
 The sidereal orbital period of a planet is measured with respectThe sidereal orbital period of a planet is measured with respect
to the stars, and determines the length of the planet’s year. Ato the stars, and determines the length of the planet’s year. A
planet’s synodic period is measured with respect to the Sun asplanet’s synodic period is measured with respect to the Sun as
seen from the moving Earth (e.g., from one opposition to theseen from the moving Earth (e.g., from one opposition to the
next).next).

41. Kepler’s and Newton’s Laws
 Ellipses describe the paths of the planets around theEllipses describe the paths of the planets around the
Sun much more accurately than do the circles used inSun much more accurately than do the circles used in
previous theories. Kepler’s three laws give importantprevious theories. Kepler’s three laws give important
details about elliptical orbits.details about elliptical orbits.
 The invention of the telescope led Galileo to newThe invention of the telescope led Galileo to new
discoveries, such as the phases of Venus and thediscoveries, such as the phases of Venus and the
moons of Jupiter, that supported a heliocentric view ofmoons of Jupiter, that supported a heliocentric view of
the universe.the universe.
 Newton based his explanation of the universe on threeNewton based his explanation of the universe on three
assumptions, now called Newton’s laws of motion.assumptions, now called Newton’s laws of motion.
These laws and his law of universal gravitation can beThese laws and his law of universal gravitation can be
used to deduce Kepler’s laws and to describe mostused to deduce Kepler’s laws and to describe most
planetary motions with extreme accuracy.planetary motions with extreme accuracy.

42. Kepler’s and Newton’s Laws
 The mass of an object is a measure of the amount ofThe mass of an object is a measure of the amount of
matter in it; weight is a measure of the force with whichmatter in it; weight is a measure of the force with which
the gravity of a world pulls on an object’s mass when thethe gravity of a world pulls on an object’s mass when the
two objects are at rest with respect to each other (or,two objects are at rest with respect to each other (or,
equivalently, how much the object pushes down on aequivalently, how much the object pushes down on a
scale).scale).
 The path of one astronomical object around another,The path of one astronomical object around another,
such as that of a comet around the Sun, is an ellipse, asuch as that of a comet around the Sun, is an ellipse, a
parabola, or a hyperbola. Ellipses are bound orbits, whileparabola, or a hyperbola. Ellipses are bound orbits, while
objects with parabolic and hyperbolic orbits fly away,objects with parabolic and hyperbolic orbits fly away,
never to return.never to return.

43. Key TermsKey Terms
acceleration
angular momentum
aphelion
astronomical unit
configuration
conjunction
conservation of angular
momentum
conservation of linear
momentum
cosmology
direct motion
ellipse
elongation
focus (of an ellipse)
force
force law
Galilean moons
gravity
heliocentric cosmology
hyperbola
inferior conjunction
inferior planet
Kepler’s laws
kinetic energy
law of equal areas
law of inertia
law of universal
gravitation
light-year
mass
model
moment of inertia
momentum
Newton’s laws of
motion
Occam’s razor
opposition
parabola
parallax
parsec
perihelion
potential energy
retrograde motion
scientific method
scientific theory
semimajor axis
sidereal period
superior conjunction
superior planet
synodic period
theory
universal constant of
gravitation
velocity
weight
work