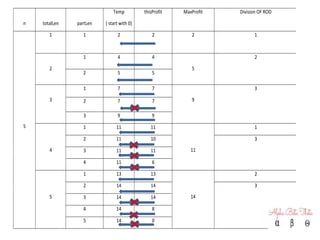
This document discusses the rod cutting problem and its solution. It contains: 1) An introduction and presentation by three students with their IDs. 2) An explanation of the rod cutting problem with a table showing length, profit, and total profit. 3) Pseudocode for the recursive solution to calculate maximum profit by cutting a rod into pieces of different lengths. 4) Analysis of the time complexity of the recursive solution as O(n^2).

2. Presented By
MD. Sad Adnan 162-15-7814
Quazi Zayed Bin Hasan 162-15-7695
Susmita karmakar 162-15-7721

3. Quazi Zayed Bin Hasan
162-15-7695

4. Length of pieces Profit for pieces
0 0
1 2 $
2 5 $
3 9 $
4 6 $

5. 0 0 0 0 0 0
0 2 4 6 8 10
0 2 5 7 10 12
0 2 5 9 11 14
0 2 5 9 11 14
#If pieces of length is greater than the total length that’s why previous profit
and current profit are same
#If previous profit is greater than current profit that’s why we count previous
profit is the current profit
14

7. MD. Sad Adnan
162-15-7814

8. Pseudo Code
int priceOfLen[ ] = {0, 2, 5, 9, 6};
int maxProfit( n )
{
for (totalLen  1 to n)
{
tmp  0;
for (partLen  1 to totalLen)
{
thisProfit  priceOfLen[partLen] + maxProfitOfLen[totalLen - partLen];
if (tmp < thisProfit)
{
tmp  thisProfit;
partLenOfLen[totalLen]  partLen;
}
}
maxProfitOfLen[totalLen]  tmp;
}
return maxProfitOfLen[n];
}

9. Void Divisions( n )
{
while (n > 0)
{
print partLenOfLen[n] ;
n  n - partLenOfLen[n];
}
}
Pseudo Code For Knowing The How We Have To Cut The Rod
0 1 2 3 4 5
priceOfLen[ ]
maxProfitOfLen[ ]
partLenOfLen[ ]

10. n totalLen partLen
Temp
( start with 0)
thisProfit MaxProfit Division OF ROD
5
1 1 2 2 2 1
2
1 4 4
5
2
2 5 5
3
1 7 7
9
3
2 7 7
3 9 9
4
1 11 11
11
1
2 11 10 3
3 11 11
4 11 6
5
1 13 13
14
2
2 14 14 3
3 14 14
4 14 8
5 14 0

11. Susmita karmakar
162-15-7721

12. Time complexity

13. T(n) = T(n-1) + T(n-2) +…..+T(1) +
1T(1)=1T(2) = T(1) + 1= 2T(3) = T(2) + T(1)+
1 = 2 + 1 + 1 T(n) = n + n-1 + n-2 + … in an
Arithmetic ProgressionT(n) = O(n²)
The run time complexity is T(n)=O(n²).