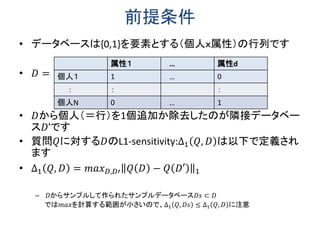
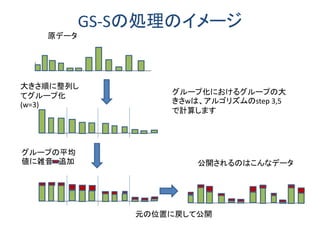
パーソナルデータの入ったデータベースを匿名化して第3者に渡す場合の議論が巷では多いようです。しかし、ビッグデータが超ビッグになり、時間的に累積してくる時系列データのような場合、データベース全体を第3者に渡す方法はだんだん現実的でなくなります。
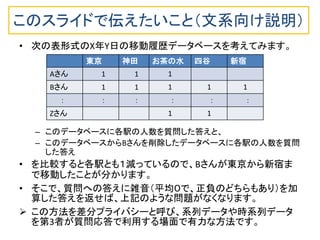
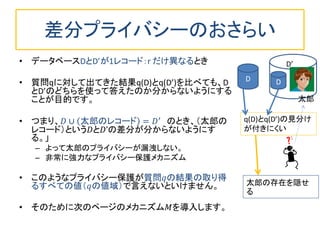
データベースへ利用者が質問する使い方だと、質問への回答から個人情報が漏れなければ、安全性が高いわけです。そのための技術として使えそうなのが、ここで述べる差分プライバシーです。
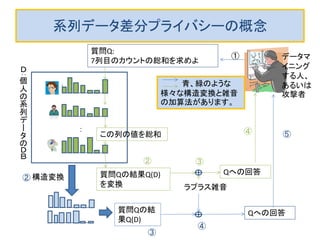
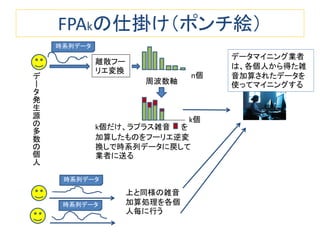
このスライドでは、(1)差分プライバシーの基礎入門と、(2)差分プライバシーを時系列データに適用する方法に関する最近の4本の論文を紹介します。