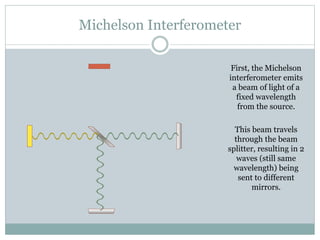
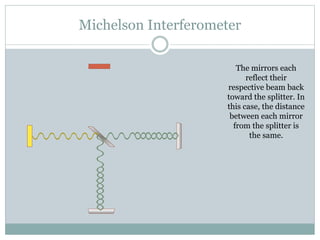
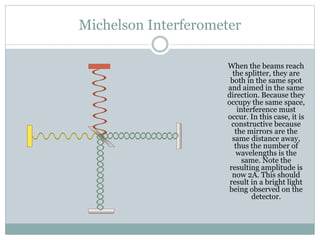
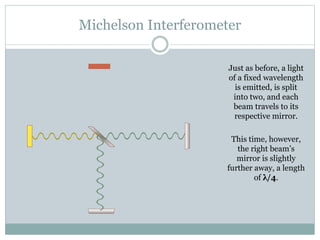
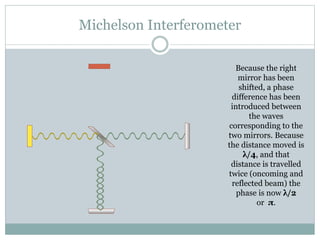
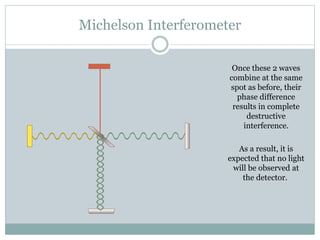
The Michelson interferometer works by emitting a beam of light from a source, splitting it using a beam splitter into two beams that travel to different mirrors and are reflected back. When the paths of the two beams are the same length, constructive interference occurs and a bright light is detected. However, when one mirror is moved by a quarter wavelength, a phase difference is introduced that causes complete destructive interference and no light is detected. The Michelson interferometer thus demonstrates interference by introducing path length differences between split beams.

1. S H A A N A R O E S T E
P H Y S 1 0 1 – L M 2
Michelson Interferometers

2. Michelson Interferometer
The following is an explanation of how and why a Michelson
interferometer works. This learning object assumes a
previous understanding of the basics of light waves.

3. Michelson Interferometer
A Michelson interferometer is used to observe interference.
It does this through a setup involving a light source, a light
detector, a beam splitter, and mirrors.
By splitting the beam of light and introducing differences in
path length for the resulting beams, interference can be
induced.

4. Michelson Interferometer
The following slides will explain this concept in greater detail.
Legend
Light wave (original)
Light wave (split)
Light wave (recombined)
Mirror
Light source
Beam splitter
Light detector

5. Michelson Interferometer
First, the Michelson
interferometer emits
a beam of light of a
fixed wavelength
from the source.
This beam travels
through the beam
splitter, resulting in 2
waves (still same
wavelength) being
sent to different
mirrors.

6. Michelson Interferometer
The mirrors each
reflect their
respective beam back
toward the splitter. In
this case, the distance
between each mirror
from the splitter is
the same.

7. Michelson Interferometer
When the beams reach
the splitter, they are
both in the same spot
and aimed in the same
direction. Because they
occupy the same space,
interference must
occur. In this case, it is
constructive because
the mirrors are the
same distance away,
thus the number of
wavelengths is the
same. Note the
resulting amplitude is
now 2A. This should
result in a bright light
being observed on the
detector.

8. Michelson Interferometer
Now let’s modify the experimental settings by moving the
right mirror to the right by λ/4
(one quarter of the beam’s wavelength)

9. Michelson Interferometer
Just as before, a light
of a fixed wavelength
is emitted, is split
into two, and each
beam travels to its
respective mirror.
This time, however,
the right beam’s
mirror is slightly
further away, a length
of λ/4.

10. Michelson Interferometer
Because the right
mirror has been
shifted, a phase
difference has been
introduced between
the waves
corresponding to the
two mirrors. Because
the distance moved is
λ/4, and that
distance is travelled
twice (oncoming and
reflected beam) the
phase is now λ/2
or π.

11. Michelson Interferometer
Once these 2 waves
combine at the same
spot as before, their
phase difference
results in complete
destructive
interference.
As a result, it is
expected that no light
will be observed at
the detector.

12. Michelson Interferometer
I hope this helped to elucidate the functionality and
underlying theory of this ingenious device.
Thank you for reading.