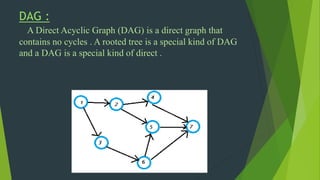
This document presents information about Directed Acyclic Graphs (DAGs): 1) A DAG is a directed graph that contains no cycles. It can be used to represent common subexpressions in a compiler by only compiling a subexpression once but using its value multiple times. 2) DAGs can also represent prerequisites in a university course schedule or constraints in a construction project, with edges drawn from nodes a to b whenever a occurs before b. 3) Partial orders used to prevent cycles in DAGs must be transitive and non-reflexive.

1. Presentation on Direct
Acyclic Graph (DAG)
Ranada Prasad Shaha University
Course Title : Compiler Design
Course code : CSE 333
Submitted by :
Rubyyat Abir
ID : 15100002
Dept : CSE

2. DAG :
A Direct Acyclic Graph (DAG) is a direct graph that
contains no cycles . A rooted tree is a special kind of DAG
and a DAG is a special kind of direct .

3. Continue :
 A DAG may be used to represent common
subexpressions in an optimizing compiler.
 Example :
 expression : a*b+f(a*b)
 The common subexpression a*b need only be compiled
 Once but its value can be used twise.


4. A Dag can be used to represent prerequisites in a
University course , constraints on operations to be
Carried out in building construction, in fact an
arbitrary partial order ‘<’ . An edge is drawn from
a to b whenever a<b. A partial order ‘<’ satisfies :
i) transitivity, a<b and b<c implies a<c
ii) non-reflexive , not (a<a)

5.  These condition prevent cycles because v1<v2…<vⁿ<v1
 Would imply that v1<v1 . The word ‘partial’ indicates
 That not every pair or values are ordered. Examples of
 Partial orders are numerical less-than (also a total
order) and ‘subset-of’ ; note that {1,2} is a subset of
 {1,2,3} but that {1,2} and {2,3} are incomparable , i.e
 There is no order relationship between them .