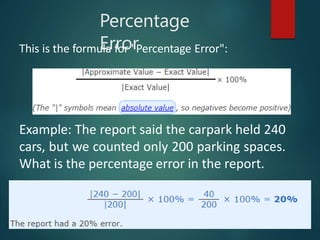
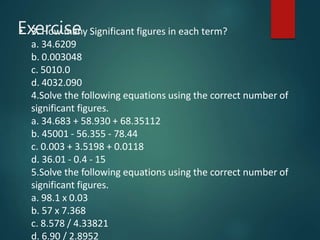
Dimensional analysis can be used to derive equations, check if equations are dimensionally correct, and find the dimensions or units of derived quantities. It involves identifying the fundamental dimensions - such as length, time, mass - of the variables in an equation. An equation is dimensionally correct if the dimensions on both sides are equal. For example, the equation for velocity, v=s/t, can be dimensionally checked as [v]=[s]/[t] which gives meters/second. Dimensional analysis allows deriving the formula for the period of a pendulum as T=2π√(l/g).

1. CHAPTER 1.3: DIMENSIONS
CHAPTER 1.3
DIMENSIONALANALYSIS

2. Grab the whole picture !
Measurements Quantities
Units Instruments Scalar Quantities
Vector Quantities
Accuracy & Uncertainty
Dimension
Analysis Significant Figures
DIMENSIONAL ANALYSIS

3. DIMENSIONS
What is “Dimension” ?

4. Many physical quantities can be expressed in terms of a
combination of fundamental dimensions such as
[Length] L
[Time] T
[Mass] M
[Current] A
[Temperature] θ
[Amount] N
The symbol [ ] means dimension or stands for dimension

5. There are physical quantities which are dimensionless:
numerical value
ratio between the same quantity angle
some of the known constants like ln,
log and etc.

6. Dimensional Analysis
Dimension analysis can be used to:
Derive an equation.
Check whether an equation is dimensionally
correct. However, dimensionally correct doesn’t
necessarily mean the equation is correct
Find out dimension or units of derived quantities.

7. Derived an Equation (Quantities)
Example 1
Velocity = displacement / time
[velocity] = [displacement] / [time]
= L / T
= LT-1
v = s / t

8. Example 2
 The period P of a swinging pendulum depends only on
the length of the pendulum l and the acceleration of
gravity g.
 What are the dimensions of the variables?
● t → T
● m → M
● ℓ → L
● g → LT-2
The period of a pendulum

9. Write a general equation:
By using the dimension method, an expression could be
derived that relates T, l and g
T α ma ℓbgc
whereby a, b and c are dimensionless constant
thus
T = kma ℓbgc

10. Write out the dimensions of the variables
= MaLb(LT-2)c
= MaLbLcT-2c
[T] = [ma][ℓb][gc]
T1 = MaLb+cT-2c
Using indices
a = 0
-2c = 1 → c =-½
b + c = 0
b = -c = ½

11. T = kma ℓbgc
T = km0 ℓ½g-½
g
l
T  k
Whereby, the value of k is known by experiment

12. Exercises
The viscosity force, F going against the movement of a
sphere immersed in a fluid depends on the radius of
the sphere, a the speed of the sphere, v and the
viscosity of the fluid, η. By using the dimension
method, derive an equation that relates F with a, v and
η.
(given that )
Av
 
Fl

13. To check whether a specific formula or
an equation is homogenous
Example 1
S = vt
[s] = [v] [t]
L.H.S
[s] = L
R.H.S
[v] [t] = LT-1(T)
= L
Thus, the left hand side = right hand side, renderingthe
equation as homogenous

14. m
C 
[m]
Example 2
Given that the speed for the wave of a ropeis
F
,
m
[C]2

[F]
Check its homogenity by using the dimensionalanalysis
C 2

F

15. L.H.S
[C] = (LT-1)2
[C] = L2T-2
R.H.S
[F] = MLT-2 ,
[M ] M
[F] MLT2
 = LT-2
[M] = M
Conclusion: The above equation is not homogenous
(L.H.S ≠ R.H.S)

16. Exercises
Show that the equations below are
either homogenous or otherwise
v = u + 2as
s = ut + ½ at2

17. Find out dimension or units of derived
quantities
k
T 2
 2 m
k
m
T  2
Example
Consider the equation ,
where m is the mass and T is a time, therefore dimensionof
k can be describe as
k
m
T  2

18. T2
k 
2m
[T2
]
[k] 
[m]

M
T2
 MT2
→ unit: kgs-2
thus, the units of k is inkgs-2

19. Exercise
The speed of a sound wave, v going through an
elastic matter depends on the density of the
elastic matter, ρ and a constant E given as
equation
V = E½ - ρ-½
Determine the dimension for E in its SI units

20. DimensionalAnalysis
Example:
The period P of a swinging pendulum depends only on
the length of the pendulum l and the acceleration of
gravity g. Which of the following formulas for P could
be correct ?
l
g
l
g
P2
(a) (b) (c) P 2
Given: d has units of length (L) and g has units of (L / T 2).
P = 2 (lg)2

21. Dimensional Analysis
Example continue…
Realize that the left hand side P has units of time (T )
● Try the first equation
P  2dg2
(a) (b) (c)
(a)
 L 
2
L4

L 
T 2 

T 4  T Not Right !!
d
g
P  2
g
P  2 d

22. L
T2
L
 T2
 T
P  2dg2
(a) (b) (c)
(b) Not Right !!
Dimensional Analysis
Example continue…
Try the second equation
d
g
P  2
g
P  2 d

23. L
L
T 2
T 2
 T

P  2dg2
(a) (b) (c)
(c) This has the correct units!!
This must be the answer!!
Dimensional Analysis
Example continue…
Try the third equation
d
g
P  2
g
P  2 d

24. • True value – standard or reference of known value or a
theoretical value.
• Accuracy: This is the closeness of the measured
values to the true value.
• Precision: reproducibility or agreement with each other
for multiple trials. It is the closeness of the measured
values to each other: the closer they are to each other,
the more precise they are.
• Uncertainty: The interval in which the true value lies is
called the uncertainty in the measurement.
• Absolute Uncertainty or ± value
• The absolute uncertainty in the mean value of
measurements is half the range of the measurements.
Some terminology

25. Error calculation of
Uncertainty
• E.g.
• Suppose the measurements of the diameter of a pin by
a Vernier Caliper are as follows:
• 0.25mm; 0.24mm;0.26mm; 0.23mm;0.27mm;
• Solution
• The mean = (0.25 + 0.24 + 0.26 + 0.23 + 0.27)/5 =125/5
= 0.25mm
• The range = 0.27 - 0.23 = 0.04mm
• Absolute Uncertainty = ± 0.04/2 = ± 0.02
• So, the mean value = mean ± range/2
= 25 ± 0.04/2
= 25 ± 0.02

26. Combining uncertainties + and -
• Adding or subtracting quantities then sum all
individual absolute uncertainties
• eg 2.1 ± 0.1 + 2.0 ± 0.2 = 4.1 ± 0.3
• eg 2.1 ± 0.1 - 2.0 ± 0.2 = 0.1 ± 0.3
this method overestimates the final uncertainty
Error calculation of
Uncertainty

27. Rule: percentage uncertainty are added
Estimated uncertainty is written with a ± sign;
for example: 8.8 ± 0.1 cm
Percent uncertainty is the ratio of the uncertainty
to the measured value, multiplied by 100:
© 2014 Pearson Education,Inc.
Error calculation of
Uncertainty

28. When Dividing or multiplying quantities, then sum all of
the individual relative uncertainties
• eg (2.5 ± 0.1) x (5.0 ± 0.1)
• = (2.5 ± 4%) x (5.1 ± 2%) =12.5 ± 6% (or 0.75 or 0.7)
• eg (5.2 ±0.1) / (0.84 ± 0.05)
• 5.2/0.84 =6.19 = 6.2
• Find % uncertainty: (0.1/5.2)x100 = 1.92 = 2
• (0.05/0.84)x100 = 5.95 = 6
• Sum of % uncertainty = 2%+6% = 8%
• Absolute uncertainty =(8/100)x6.2=0.496 =0.5
• = 6.2 ± 0.5 or 6.2 ± 8%
Error calculation of
Uncertainty

29. Significant Figures
The rules of significant figures:
1. Any figures that is non-zero, are considered as a
significant figure.
2.Zeros at the beginning of a number are notsignificant
Example: 0.254 ----------------- 3 s.f
3.Zeros within a number are significant.
Example: 104.6 m ---------------- 4 s.f
4. Zeros at the end of a number after the decimal pointare
significant.
Example: 27050.0 ------------------- 6 s.f

30. • 5. Zeros at the end of a whole number without a decimal point
may or may not be significant.
• It depends on how that particular number was obtained,using
what kind of instrument, and the uncertaintyinvolved.
•Example:500m ------------------- could be 1 or 3sf.
Convert the unit:
• 500m = 0.5km (would you say it has 1 sf ? )
• 500m = 50 000cm (would you say it has 1 or 5 sf ?)
How to solve this problem ?
Significant Figures
…

31. Addition and Subtraction processes
The rule:
• The final result of an addition and/or subtraction
should have the same number of significant
figures as the quantity with the least number of
decimal places used in the calculation.
• Example:
• 23.1 + 45 + 0.68 + 100 = 169
• Example:
• 23.5 + 0.567 + 0.85 = 24.9
Significant
figures

32. Multiplication and division processes
The rule:
• The final result of an multiplication and/or division
should have the same number of significant figures
as the quantity with the least number of significant
figures used in the calculation.
• Example:
• 0.586 x 3.4 = 1.9924
= 2.0
• Example:
• 13.90 / 0.580 = 23.9655
= 24.0
Significant
figures

33. Percentage
Error
This is the formula for "Percentage Error":
Example: The report said the carpark held 240
cars, but we counted only 200 parking spaces.
What is the percentage error in the report.

34. Exercis
e
1) You measure a block with a ruler that has a precision of 1mm. You
obtain a length of 2.4cm.
• a) What is the absolute uncertainty in this measurement?
• b) What is the percentage uncertainty in this measurement?
2) The following range of results is obtained for the mass of a bouncy
ball: 13.2g, 13.4g, 13.3g, 13.4g, 13.2g, 13.3g
• a) Calculate a value for the mass of the bouncy ball.
• b) What is the absolute uncertainty in these measurements?
• c) What is the percentage uncertainty in these measurements?

35. • 3. How many Significant figures in each term?
a. 34.6209
b. 0.003048
c. 5010.0
d. 4032.090
4.Solve the following equations using the correct number of
significant figures.
a. 34.683 + 58.930 + 68.35112
b. 45001 - 56.355 - 78.44
c. 0.003 + 3.5198 + 0.0118
d. 36.01 - 0.4 - 15
5.Solve the following equations using the correct number of
significant figures.
a. 98.1 x 0.03
b. 57 x 7.368
c. 8.578 / 4.33821
d. 6.90 / 2.8952
Exercise