This document discusses various digital image processing techniques including dithering, warping, morphing, and view morphing. Specifically, it describes:
- Dithering techniques like thresholding, ordered dithering, and error diffusion to simulate colors not in the palette.
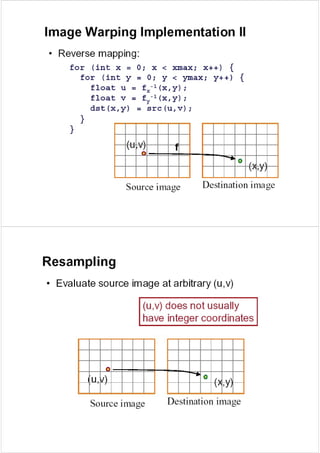
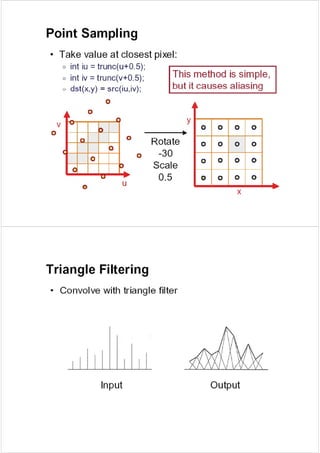
- Image warping methods like affine, projective, and bilinear mappings to rearrange pixel positions.
- Morphing as a process to create a smooth transition between two images using warping, color interpolation, and cross-dissolving.
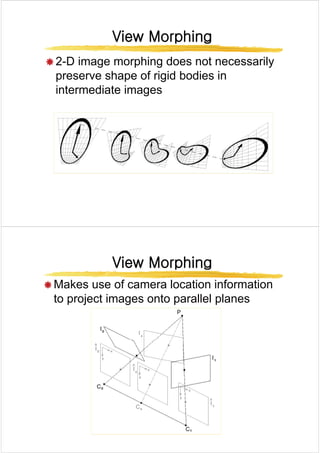
- View morphing which uses camera position to project images and preserve rigid body shapes during morphing.



![Random Dithering
Random Dithering
Random Dithering
Random Dithering
Æ Add a random amount to each pixel before thresholding
p g
Æ Typically add uniformly random amount from [-a,a]
Æ Pure addition of noise to the image
Æ Not good for black and white, but OK for more colors
Æ Add a small random color to each pixel before finding the
l t l i th t bl
closest color in the table
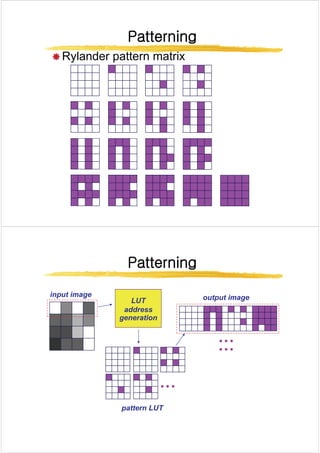
Ordered Dithering
Ordered Dithering
Ordered Dithering
Ordered Dithering
Æ Break the image into small blocks
Æ Define a threshold matrix
Æ Use a different threshold for each pixel of the block
Æ Compare each pixel to its own threshold
Æ The thresholds can be clustered, which looks like a
(di it l) h lft i
newspaper: (digital) halftoning
Æ The thresholds can be “random” which looks better](https://image.slidesharecdn.com/digitalimageprocessingdigitalimageprocessingdithering-230315045802-ea0d0f37/85/Digital_Image_Processing_Digital_Image_Processing_Dithering_-pdf-5-320.jpg)






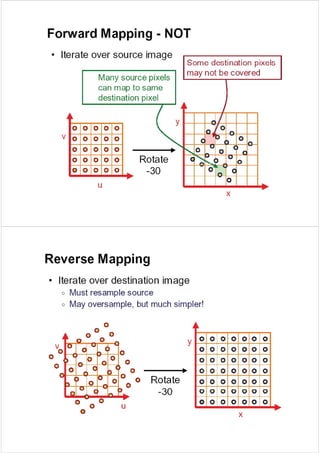
![Bilinear Interpolation
Bilinear Interpolation
Bilinear Interpolation
Bilinear Interpolation
Æ A B C D are intensity s )
1
( s
A B
E
Æ A,B,C,D are intensity
values t
s )
1
( s
−
A B
E
sB
A
s
E +
−
= )
1
( )
1
( t
G
sD
C
s
F
sB
A
s
E
+
−
=
+
)
1
(
)
1
( )
1
( t
−
C D
tF
E
t
G +
−
= )
1
(
[ ] [ ]
sD
C
s
t
sB
A
s
t +
−
+
+
−
−
= )
1
(
)
1
(
)
1
(
C D
F
[ ] [ ]
tsD
C
s
t
sB
t
A
s
t
sD
C
s
t
sB
A
s
t
+
−
+
−
+
−
−
=
+
+
+
=
)
1
(
)
1
(
)
1
)(
1
(
)
1
(
)
1
(
)
1
(](https://image.slidesharecdn.com/digitalimageprocessingdigitalimageprocessingdithering-230315045802-ea0d0f37/85/Digital_Image_Processing_Digital_Image_Processing_Dithering_-pdf-17-320.jpg)