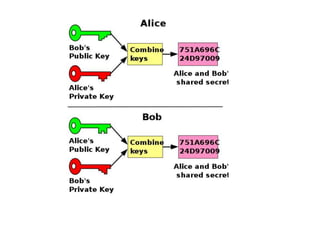
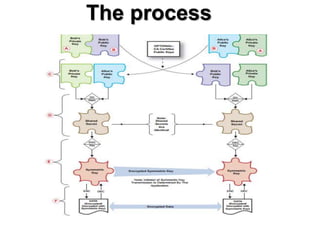
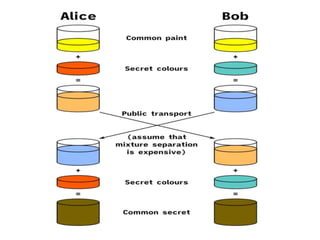
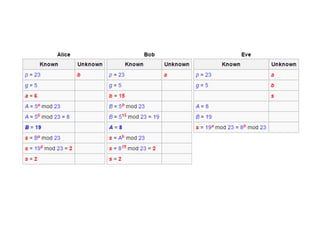
Diffie-Hellman key exchange is a cryptographic protocol that allows two parties to establish a shared secret over an unsecured communication channel. It was one of the first practical examples of key exchange and predates public-key infrastructure. The security of the Diffie-Hellman protocol relies on the difficulty of calculating discrete logarithms, though it lacks authentication and is susceptible to man-in-the-middle attacks. While an important historical algorithm, Diffie-Hellman may not scale sufficiently for future needs as key sizes would need to continually increase over time to maintain security levels.

1. Diffie-Hellman: Key
Exchange and Public
Key Cryptosystems
Supervisor:- DR. Lutfi Khanbri
Rania Nasser Abdualqader Alhafrah
Reg.No: MITE02218 MIT

2. Introduction
Diffie–Hellman key exchange is a
mathematical method of securely
exchanging cryptographic keys over a
public channel and was one of the first
public-key protocols as conceived by
Ralph Merkle and named after that by
Whitfield Diffie and Martin Hellman.

3. DH is oneof the earliest practicalexamplesof
publickey exchangeimplementedwithinthe
field of cryptography.Publishedin 1976by
Diffieand Hellman, thisis the earliest publicly
knownworkthat proposedthe idea of a
privatekey and a correspondingpublic key.

4. History
The primaryresearchers to find and publish
the ideas of Public Key Cryptologywerefound
by WhiteldDiffeand Martin Hellman from
StanfordUniversity,
and RalphMerkle from the Universityof
California.

5. Assofrequentlyhappensintheexperimentalworld,
thetwogatheringswereworkingon thesameissue-
DiffieandHellmanonpublickey cryptographyand
Merkle onpublickey distribution-whentheygot to
knowaboutoneanother'sworkandacknowledged
therewascollaborationintheirmethodologies.In
Hellman'swords:"Weeachhada keypieceofthe
puzzlekeepinginmindit'sactual oneofusfirst
saidX, andanother ofusfirstsaidY, andsoon,it
wasthecombinationofforwardandbackward
betweenusthat permittedthedisclosure.."

6. What is Diffie – Hellman?
Is an algorithm to enable two usersto
securelyexchangea key that can then be
usedfor subsequentencryptionof
messages.The Diffie-Hellmanalgorithm
dependsfor its effectivenesson the
difficultyof computingdiscrete
alogarithms.

8. The Diffie-Hellman Key Exchange Algorithm

9. Primitive Roots
𝑎 is a primitive root of 𝑞 if:
𝑎 mod 𝑞, 𝑎2
mod 𝑞, 𝑎3
mod 𝑞 ………………
𝑎𝑞−1
mod 𝑞 are distinct
and congruent to a power of 𝑎 .

10. Example 1: Is 2 a primitive of
prime number 5?
𝟐𝟏 mod 5 𝟐 mod 5 2 
𝟐𝟐
mod 5 𝟒 mod 5 4 
𝟐𝟑 mod 5 𝟖 mod 5 3 
𝟐𝟒 mod 5 𝟏𝟔 mod 5 1 
Yes, 2 is a primitive of prime number 5

11. Algorithm
Example 1: Is 2 a primitive of
prime number 7?
𝟐𝟏 mod 7 𝟐 mod 7 2 
𝟐𝟐 mod 7 𝟒 mod 7 4 
𝟐𝟑 mod 7 𝟖 mod 7 1 
𝟐𝟒
mod 7 𝟏𝟔 mod 7 1 
𝟐𝟓 mod 7 32 mod 7 4 
𝟐𝟔 mod 7 64 mod 7 1 
No, 2 isn’t a primitive of prime number 7

12. Diffie-Hellman Correctness and its Proof
2. Bob has computed
3. Bob has

13. The process

14. Illustration with
Examples

15. Example 1
Illustration with colors

17. Example2:
The security of the Diffie-Hellman key exchange
lies in the fact that, while it is relatively easy to
calculate exponentials modulo a prime, it is very
difficult to calculate discrete logarithms. For large
primes, the latter task is considered infeasible.
Here is an example. Key exchange is based on
the use of the prime number.

18. Step 1: Alice and Bob get public numbers P = 7, G = 3
Step 2: Alice selected a private key a = 4 and
Bob selected a private key b = 5
Step 3: Alice and Bob compute public values
Alice: x =(3^4 mod 7) = (81 mod 7) = 4
Bob: y = (3^5 mod 7) = (243 mod 7) = 5
Step 4: Alice and Bob exchange public numbers

19. Step 5: Alice receives public key y =5and
Bob receives public key x = 4
Step 6: Alice and Bob compute symmetric
keys
Alice: ka = y^a mod p = 625 mod 7= 2
Bob: kb = x^b mod p = 1024 mod 7= 2
Step 7: 2 is the shared secret.

20. Coding
C#

21. Secrecy chart
The chart below depicts who knows what,
again with non-secret values in blue, and
secret values in red. Here Eve is an
eavesdropper – she watches what is sent
between Alice and Bob, but she does not
alter the contents of their communications.

23. Man-In-The-Middle Attacks

24. Advantages and
Disadvantages

25. Its advantages are
• The security factors with respect to the fact that
solving the discrete alogarithm is very challenging,
and That the shared key (the secret) is never itself
transmitted over the channel.
Its disadvantages are
• There are expensive exponential operations
involved, and the algorithm can’t be used to encrypt
messages, it uses for establishing a secret key only.

26. • There is also a lack of authentication.
• There is no identity of the parties
involved in the exchange.
• It is easily susceptible to man-in-the-
middle attacks. A third party C, can
exchange keys with both A and B, and
can listen to the communication between
A and B.
Its disadvantages (con.)

27. Future of Diffe-Hellman

28. Future of Diffe-Hellman
Diffe-Hellman is an public key algorithm,
specialists say it don't scale well for future.As of
right now it is expressed that Diffe- Hellman keys
shorter than 900 bits are not suciently secure. To
make Diffe- Hellman keys, which now can go to
1,024 bits, secure for the following 10 to 20 years,
associations would need to grow to key lengths of
no less than 2,048 bits, as per Stephen Kent,
chief researcher at BBN Technologies.In the long
run, key sizes would need to grow to 4,096 bits

29. Conclusion
Designing a Key exchange algorithm with 100%
Accuracy is not possible.
Our Algorithm ideas makes execution simpler and in
addition avoidance from common Attacks. Security
change is useful in light of
the fact that Diffie Hellman Algorithm is the premise
of a few security standards and services.

30. References
• William Stallings - Cryptography and Network Security
5th edition.
• www.youtube.com.
• Implementation of Diffie-HellmanAlgorithm-
GeeksforGeeks

31. Thank you for listening