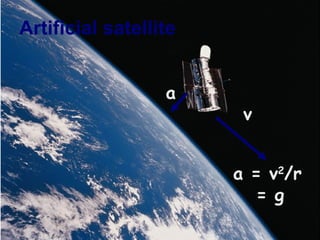
This document provides an overview of Isaac Newton's theory of universal gravitation. It discusses how Newton realized that the force causing apples to fall is the same force that causes the moon to orbit the Earth. The document then presents Newton's universal law of gravitation, which states that the gravitational force between two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. It also explains key concepts like gravitational fields and how gravity works inside planets and for artificial satellites and black holes.