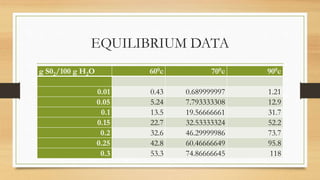
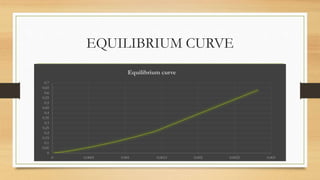
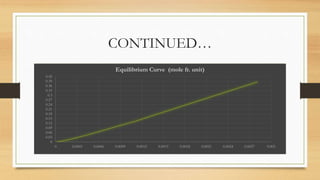
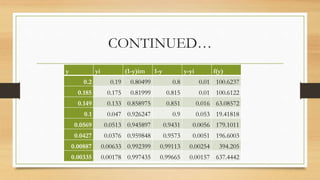
The document summarizes the design of an absorption column to remove SO2 from an air stream using water. It involves selecting water as the solvent, 1.5 inch Raschig rings as the packing material, calculating the minimum water flow rate of 116,641 kg/h, determining the flooding velocity, diameter of 1.106 m, and height of 3.88 m for the packed column. The column will treat 40,000 ft3/h of air containing 20% SO2 and recover 96% of the SO2 using 30% excess water than the minimum flow rate.

2. DESIGN OF ABSORPTION
COLUMN
PRESENTED BY: ALI SHAAN(016)
USAMA SAEED(049)
ALI HASSAN(031)

3. CASE
It is required to design a packed tower to treat 40000 ft3
/h of an air stream containing
20 mole% of so2 at 700
c and 1 atm total pressure. It is necessary to recover 96% of
the so2 using water at a rate 30% more than the minimum. The column may be
packed with
1
1
2
-inch Raschig rings and may be operated at 60% of the flooding
velocity. The individual mass transfer coefficients are / 3
xk a=1.25kmol/m s and
/ 3
yk a=0.075kmol/m s . Design the tower.

4. STEPS USED DURING DESIGN OF
ABSORPTION COLUMN
• Selection of solvent
• Selection of column type
• Selection of packing
• Equilibrium data
• Material balance
• Minimum solvent flow rate

5. CONTINUED…
• Operating solvent flow rate
• Flooding/Diameter collection
• Pressure drop
• Height of packing

6. SOLVENT SELECTION
We Selected water(H2O) here:
• Because it is cheap.
• Non Toxic.
• Easily available.

7. SELECTION OF PACKING
We have selected random packing here:
• Because pressure drop is nearly negligible in our case.
• It is cheap as compare to structured .

8. MATERIAL AND TYPE OF PACKING
Raschig ring 1.5 inches.
Ceramic material.
Because they have:
• High Strength.
• High Fracture Toughness.
• High Hardness.
• Excellent Wear Resistance.
• Good Frictional Behaviour.

9. EQUILIBRIUM DATA
g S02/100 g H2O 600c 700c 900c
0.01 0.43 0.689999997 1.21
0.05 5.24 7.793333308 12.9
0.1 13.5 19.56666661 31.7
0.15 22.7 32.53333324 52.2
0.2 32.6 46.29999986 73.7
0.25 42.8 60.46666649 95.8
0.3 53.3 74.86666645 118

10. CONTINUED…
Mole Fractions
X y
2.8124E-05 0.000908
0.000140604 0.010254
0.000281169 0.025746
0.000421694 0.042807
0.000562179 0.060921
0.000702625 0.079561
0.000843032 0.098509
0.001123727 0.137456
0.001404264 0.177456
0.00280459 0.385088

11. CONTINUED…
Mole Ratios
X Y
2.8125E-05 0.000909
0.00014062 0.010361
0.00028125 0.026426
0.00042187 0.044721
0.0005625 0.064873
0.00070312 0.086439
0.00084374 0.109273
0.00112499 0.159361
0.00140624 0.215741
0.00281248 0.626248

12. CONTINUED…
Conversion is as follows:
The equilibrium (x, y) data are converted to mole ratio unit (X, Y) and plotted on X-Y plane.
As shown below. The cure is slightly convex upward. So the operating line corresponding to
the minimum liquid rate will not touch the equilibrium line. It will rather meet the equilibrium
line at the point having an ordinate Y1 (0.25). This is the pinch point having abscissa = (X1)max
= 0.0015.
2
2
2 2
-4
so -5
so 0
0.6
( .g) 7.89x10
760
/ M.W 0.02 / 64
( . ) 5.625x10
/ M.W 100 / . 0.02 / 64 100 /18
so
atm
H
P mmHg
y e
P mmHg
c
x e g
c M W
   
   
 

13. EQUILIBRIUM CURVE
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.55
0.6
0.65
0.7
0 0.0005 0.001 0.0015 0.002 0.0025 0.003
Equilibrium curve

14. Material Balance
Average molecular weight = (mole fr. So2)*(M.W of so2)+( mole fr. Air)*(M.W of Air)
Volumetric flow rate = 40,000 ft3/h
Mass flow =m
. (.2)(64) (.8)(28.8)
35.84
M w  

31*35.84
0.07945 /
1.31443*343.15
PM
ft h
RT
  ρ
.
3 3
40,000 / *0.07945 / ftft h lb

15. CONTINUED…
1
1
1
1
1
1
1 1
2 1 1
2 2
2
3178.38 /
1441.6889 /
(1441.6889 / 35.84) kmol/ h
40.2256 /
0.2
0.25
1
(1 ) 32.180 /
8.04512 /
*(0.96) 7.7233152 /
s
G lb h
G kg h
G
G kmol h
y
y
Y
y
G G y kmol h
so entering G y kmol h
so absorbed so entering kmol h
so leaving





 

  
 
 
2 2
2 2 2
0.32180 /
/ 0.01
1 / 0.001
s
kmol h
concentration
Y so G
y Y Y

 
  

16. CONTINUED…
As solvent is pure
x2=0 (Mole Fraction unit)
X2=0 (Mole ratio unit)

17. MINIMUM LIQUID FLOW RATE
By an overall material balance:
Molecular weight of solvent =18
min 1 2
1 max 2
min
min
( )
( ) X
( ) 4984.682 /
( ) 1.3( ) 6480.0866 /
s
s
s
s operating s
L Y Y
G X
L kmol h
L L kmol h




 
6480.0886 /18
116641 /
s
s
L
L kg h



18. LIQUID FLOW RATE AT BOTTOM OF
TOWER
And the x1=0.002462
1 2 116641 7.7233 116649.2821 /sL L so absorbed kg h    

19. FLOODING VELOCITY CALCULATION
Total pressure in the tower =1atm ( I have neglected the pressure drop in the tower); temp=
303 k
L1=116649.2821 kg/h
G1=1441.6889 kg/h
M.Wav=35.84
µl=0.4079cp; surface tension = 64.47 dyne/cm (McCabe smith 7th edition)
(liquid)=61.07 lb/ft3 =978.25 kg/m3 (McCabe smith 7th edition)
3 3
0.07945 / 1.267 /g lb ft kg m ρ
ρ

20. CONTINUED…
Flow parameter
As our packing material is Raschig (dp=1.5 inch);
By using Eckert’s GPDC Chart ( Figure 5.33, principle of mass transfer and separation by
Binay k. dutta). Since it good enough for first generation packing. At flooding Flv=2.91, the
capacity parameter is 0.0075.
0.5
( ) 2.91
g
l
lv
L
F
G
 
ρ
ρ

21. The other parameters are:
Capacity parameter equation for the first generation.
1w
l

ρ
ρ
8 2
0.4079
94.5 /
4.18x10 /
l
p
c
µ cp
F ft
g ft h



CONTINUED…
2 0.2
l
( ') ( )( )w
lfl p
p
l
g c
G F µ
c
g

ρ
ρ
ρ ρ

22. CONTINUED…
2
fl
2
2
' 438.931 / .
' 0.70* ' 307 / .
' 1500 / .
op fl
op
G lb ft h
G G lb ft h
G kg m h

 


23. TOWER DIAMETER
Tower cross section:
Diameter
2
/ ' 1441.6889/1500
0.9611
opG G
m
 

0.9611*4
1.106m

 

24. TOWER HEIGHT CALCULATION
Overall material balance equation:
min 1 2
1 2
( )
X
s
s
L Y Y
G X



1
1
2
2
32.180 /
6480.0866 /
0.20
0.001547
0.001
0
s
s
G kmol h
L kmol h
y
x
y
x







25. CONTINUED…
The individual gas and liquid phase mass transfer coefficient are given. The following equation
is used to find the height.
Now we have plotted the equilibrium data on x-y plane (mole fr. Unit). Then we fined the
interfacial concentrations on the gas side. ( By Following the procedure describe in the Section
6.4.1 ( principle of mass transfer and separation process By Binay K.Dutta).
1 1
2 2
*
'
' '
(1 )
( )
(1 )*( )
tG tG
tG
y
y y
iM
tG
iy y
h H N
G
H
k a
y
N dy f y dy
y y y



 
  

26. CONTINUED…
0
0.03
0.06
0.09
0.12
0.15
0.18
0.21
0.24
0.27
0.3
0.33
0.36
0.39
0.42
0 0.0003 0.0006 0.0009 0.0012 0.0015 0.0018 0.0021 0.0024 0.0027 0.003
Equilibrium Curve (mole fr. unit)

27. CONTINUED…
y yi (1-y)im 1-y y-yi f(y)
0.2 0.19 0.80499 0.8 0.01 100.6237
0.185 0.175 0.81999 0.815 0.01 100.6122
0.149 0.133 0.858975 0.851 0.016 63.08572
0.1 0.047 0.926247 0.9 0.053 19.41818
0.0569 0.0513 0.945897 0.9431 0.0056 179.1011
0.0427 0.0376 0.959848 0.9573 0.0051 196.6003
0.00887 0.00633 0.992399 0.99113 0.00254 394.205
0.00335 0.00178 0.997435 0.99665 0.00157 637.4442

28. CONTINUED…
By using trapezoidal rule:
1 1
2 2
(1 )
( ) 12.5
(1 )*( )
12.5
y y
iM
tG
iy y
tG
y
N dy f y dy
y y y
so
N

  
 

 

29. CONTINUED…
The height of a gas-phase transfer unit:
2
2
1
2
2 2
2
'
' '
' 0.075*3600 270 / .
' 40.2256 / 0.9611 41.85371 / .
' / (1 )*0.9611 33.4824kmol/ h.m
' 37.6686kmol/ h.m
0.311
*
0.311*12.5 3.88
tG
y
y
s
tG
tG tG
G
H
k a
k kmol h m
G kmol h m
G G y
G
H m
h N H
h m

 
 
  



 

30. Specification Sheet
Identification:
Item: Packed Absorption Column
Item No: N/A
No. required: 1
Function: To remove SO2 from mixture of gases
Operation: Continuous

31. CONTINUED…
Entering gas
Kg/hr
Exit gas
Kg/hr
Liquid entering
Kg/hr
1441.6889 1045.904 116649
Design data:
No. of transfer units = 12.5
Height of transfer units = 0.311 m
Total height of column = 3.88m
Diameter = 1.109m
Pressure drop = Neglected

32. CONTINUED…
Internals:
Size and type = 1.5 in Rachig ring
Material of packing: Ceramic
Packing arrangement: Dumped
Type of packing support: Simple grid & perforated support