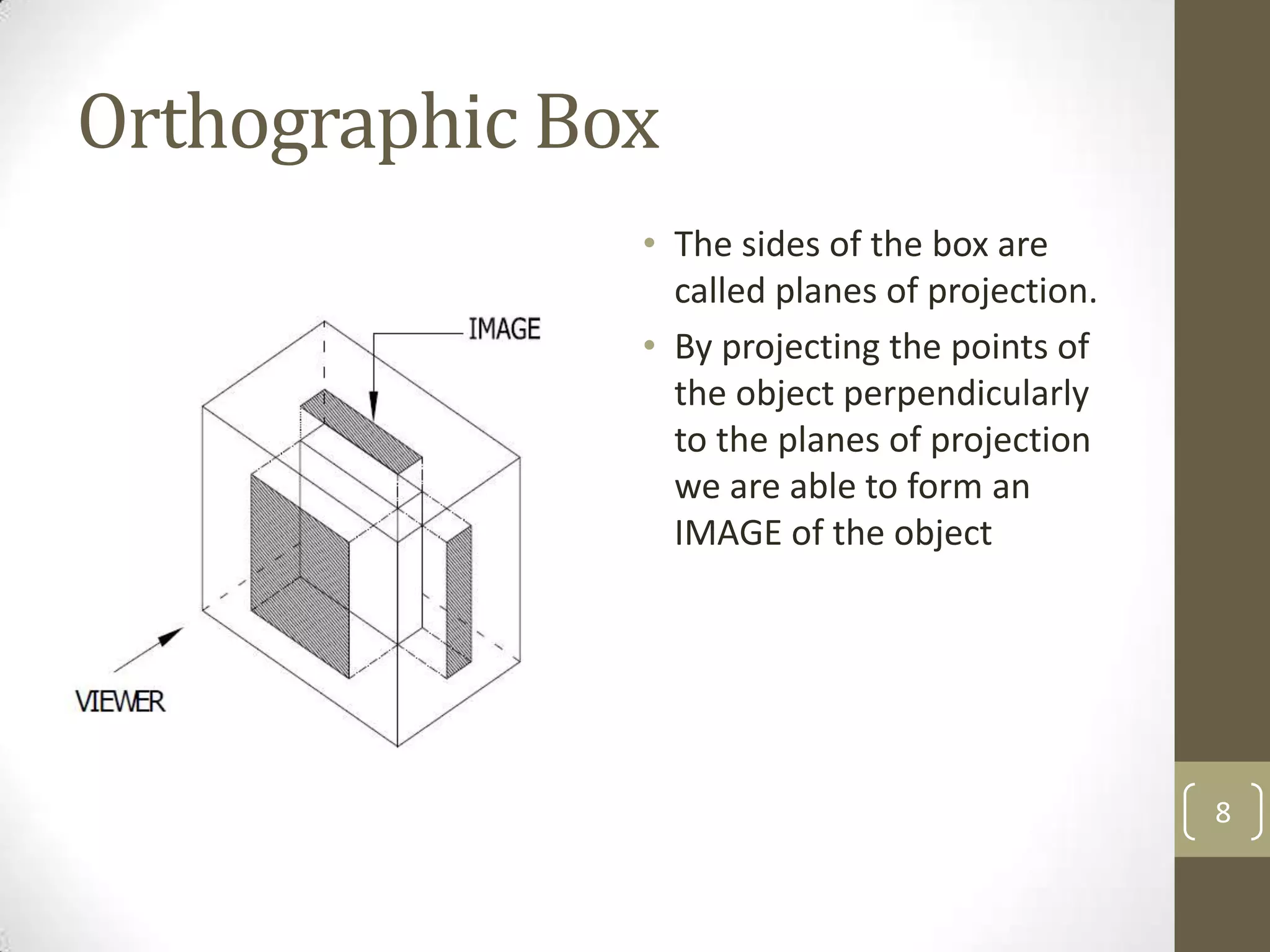
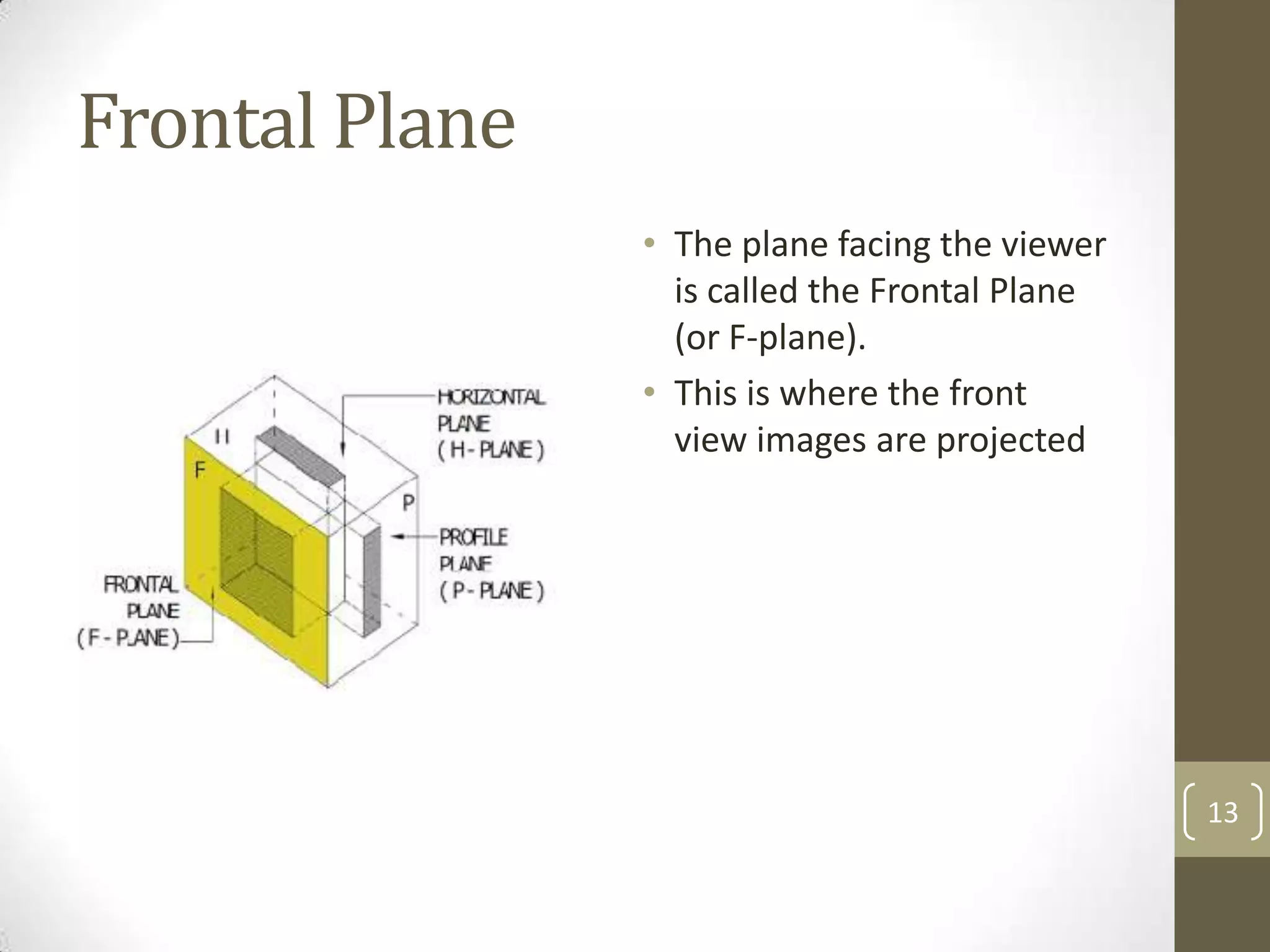
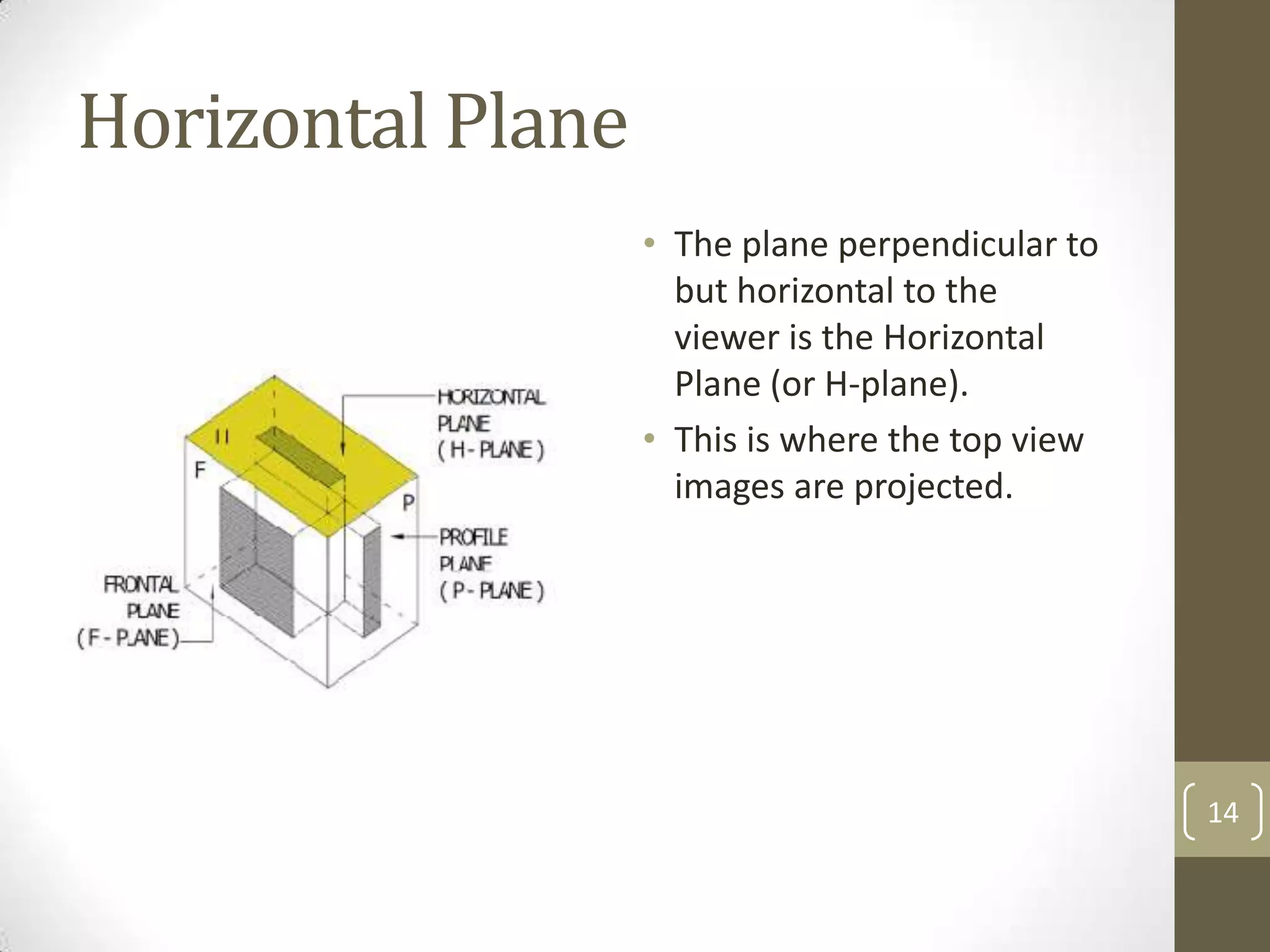
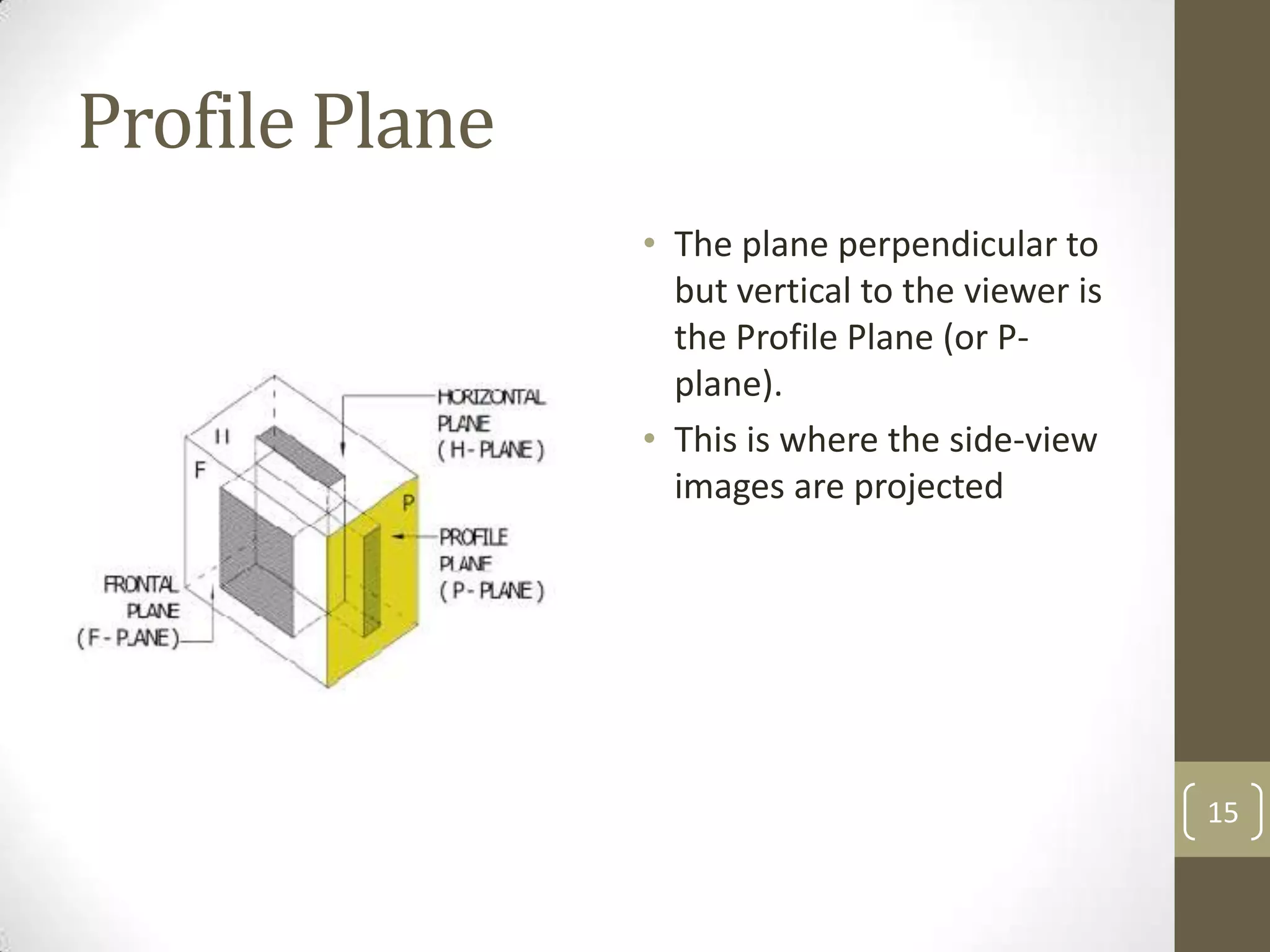
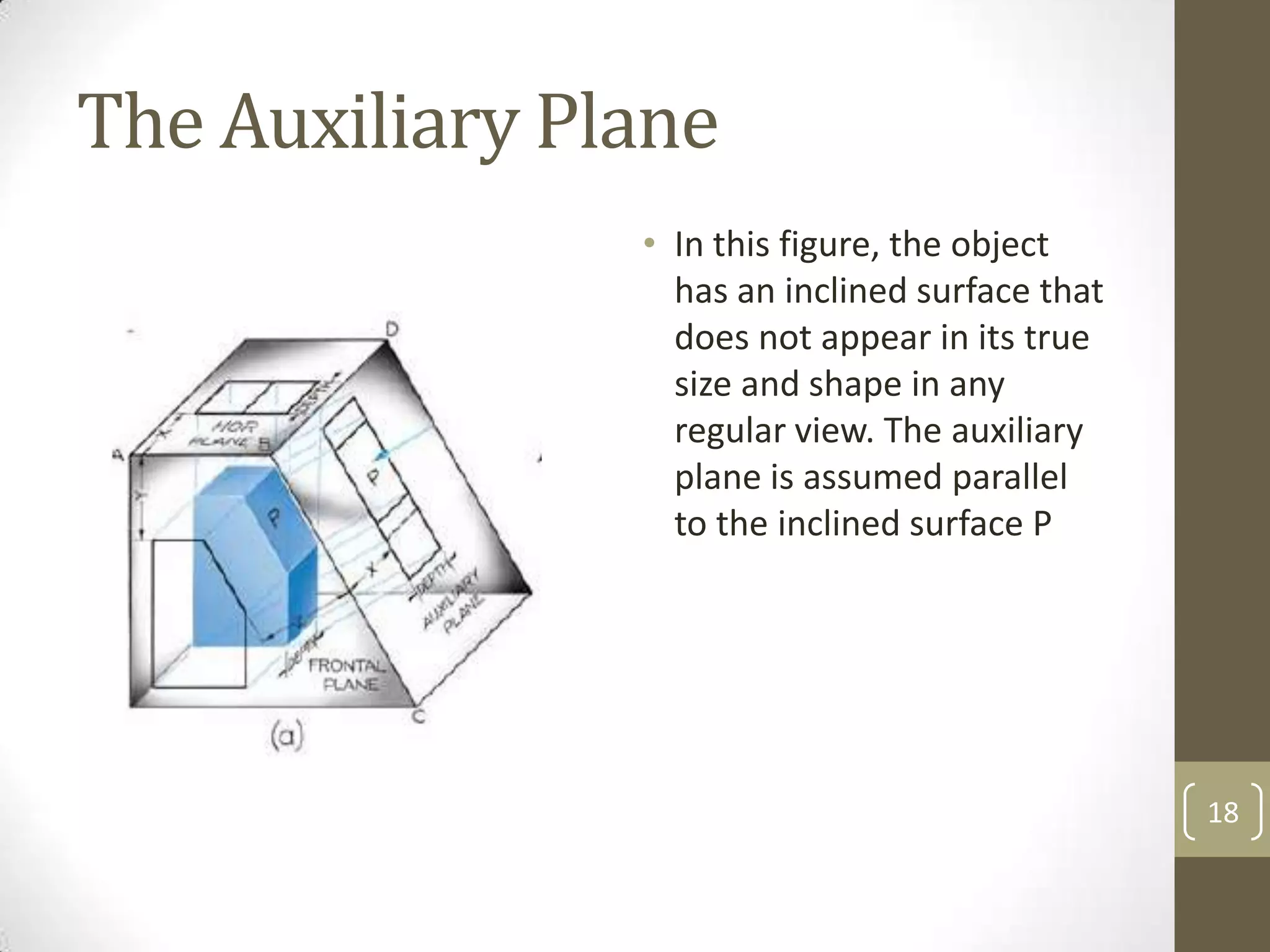
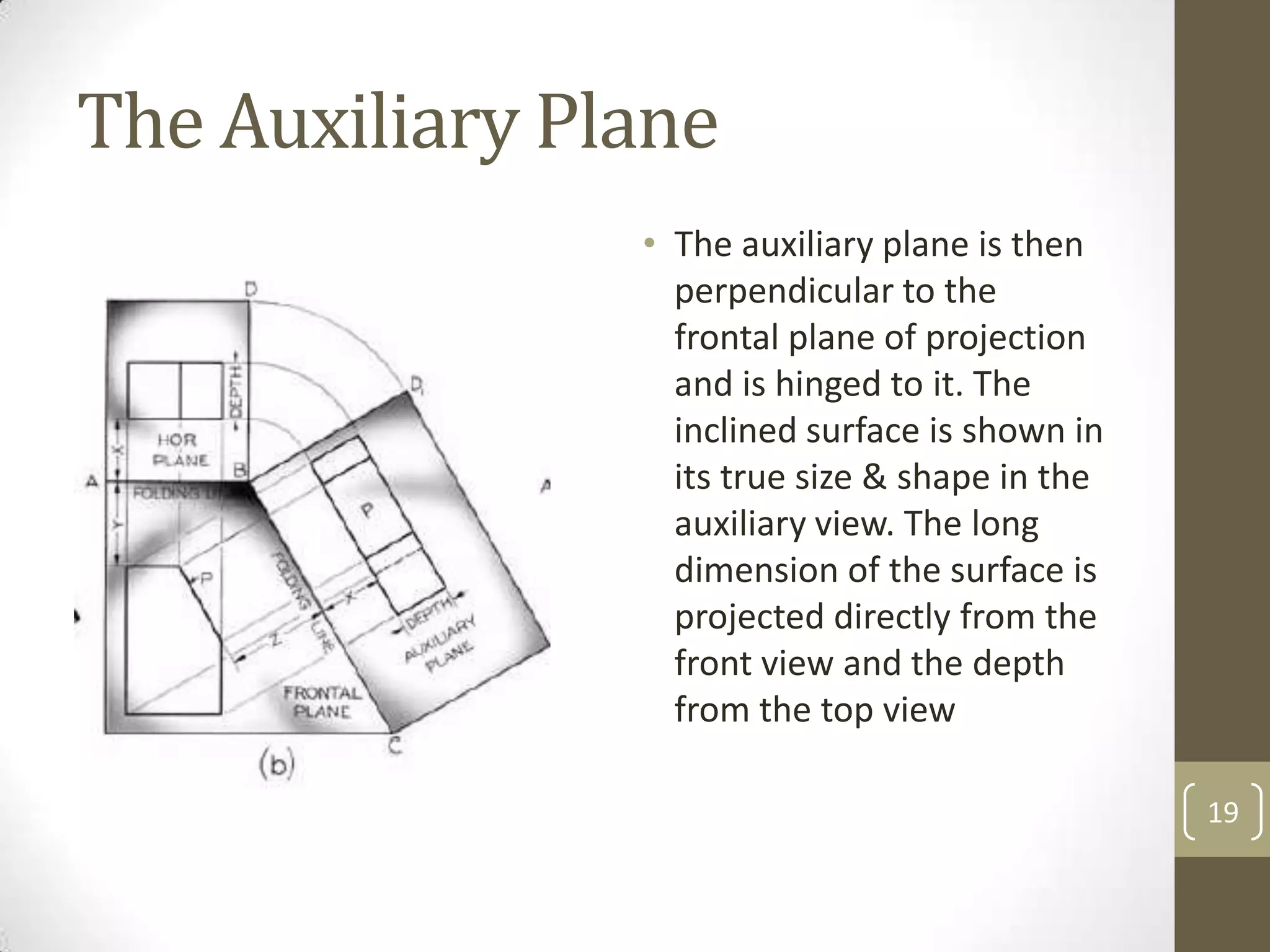
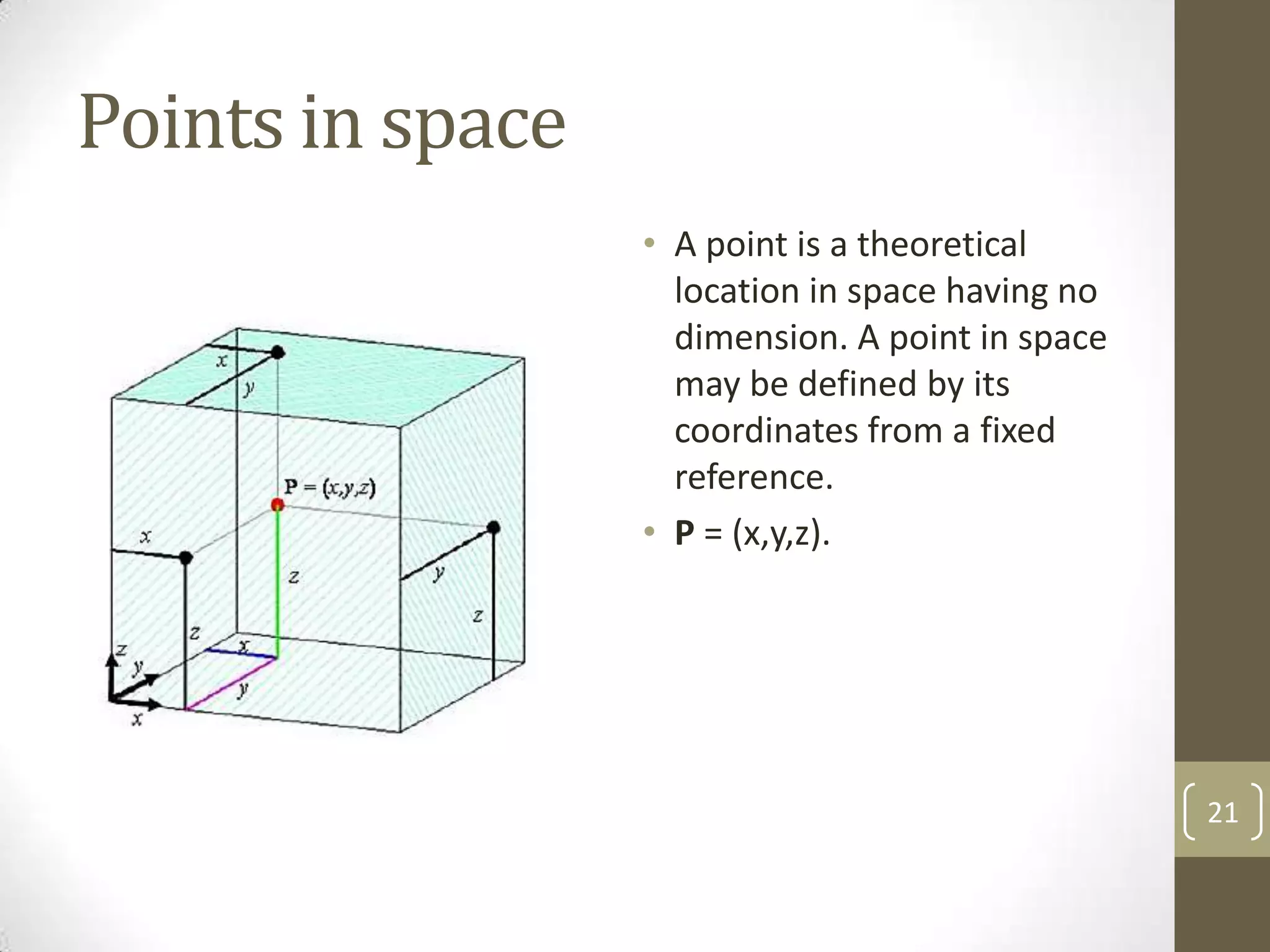
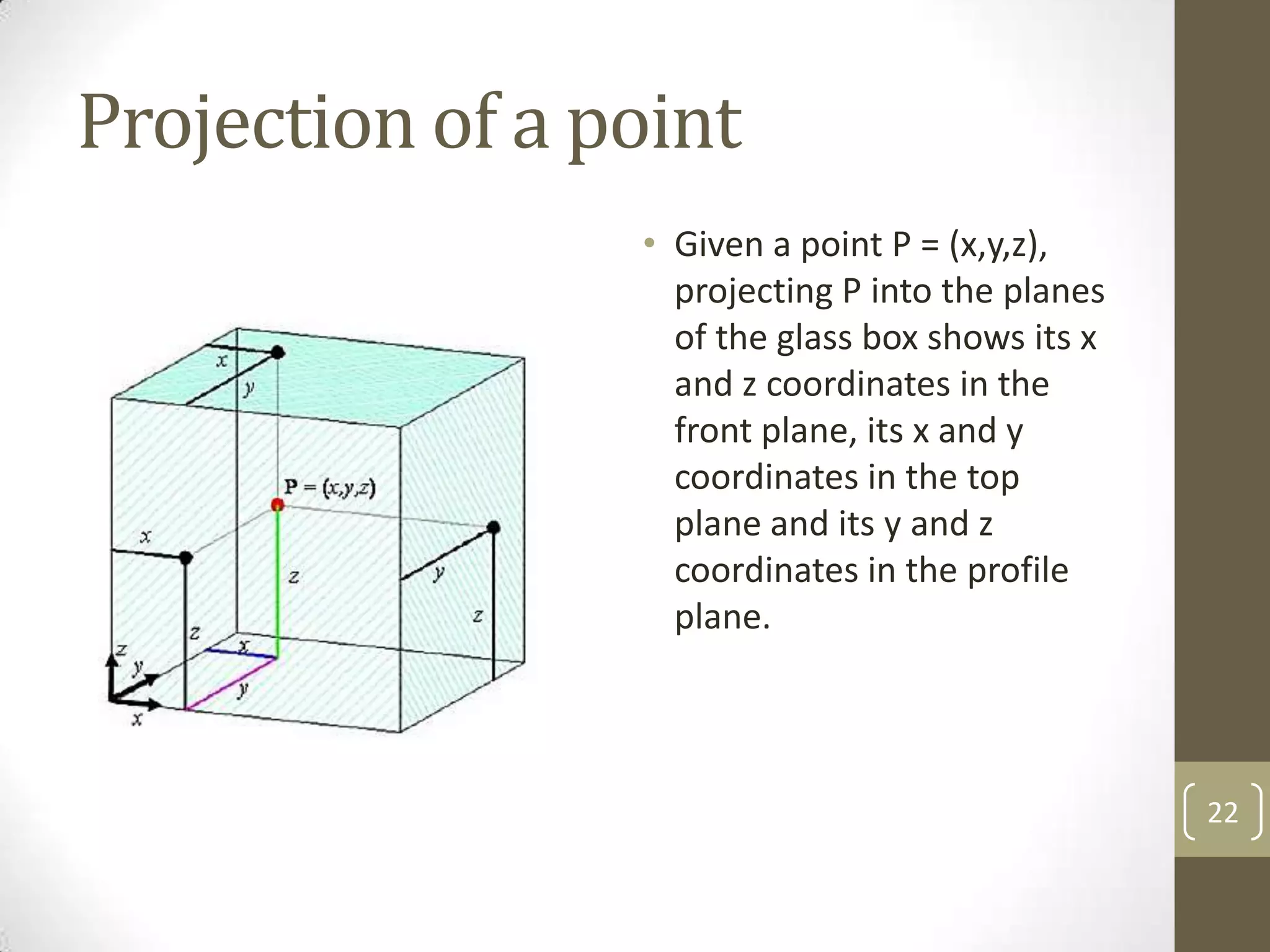
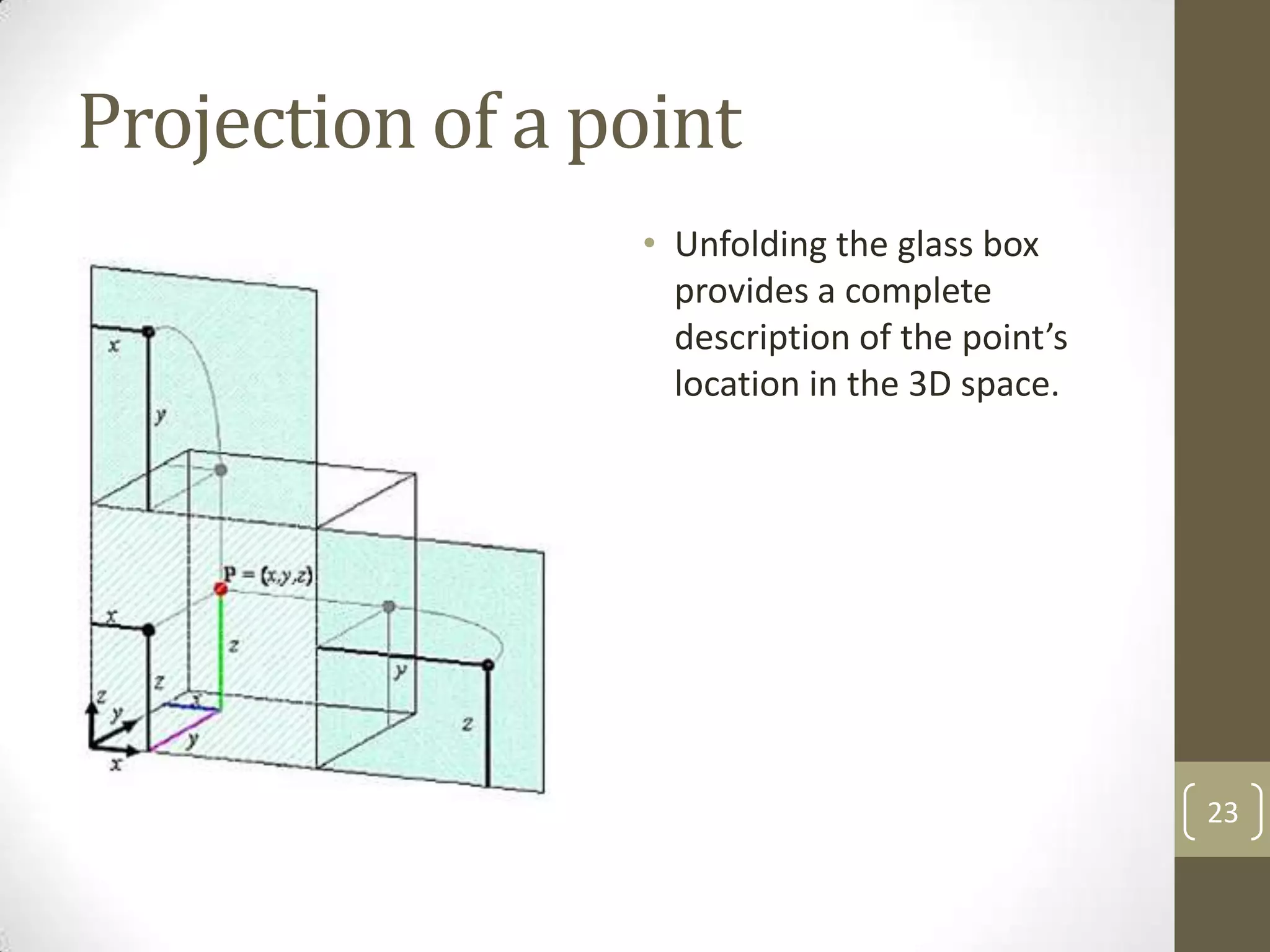
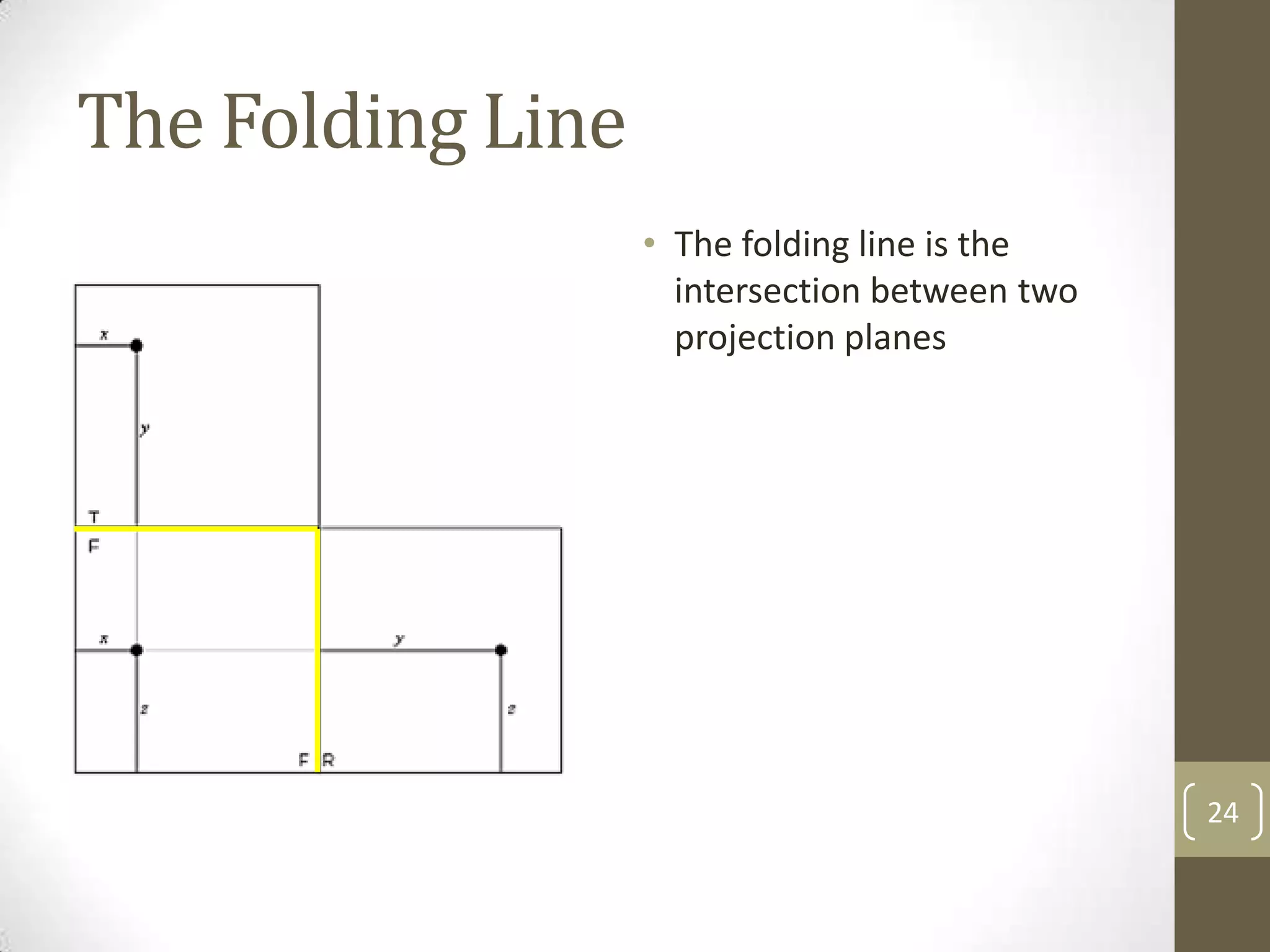
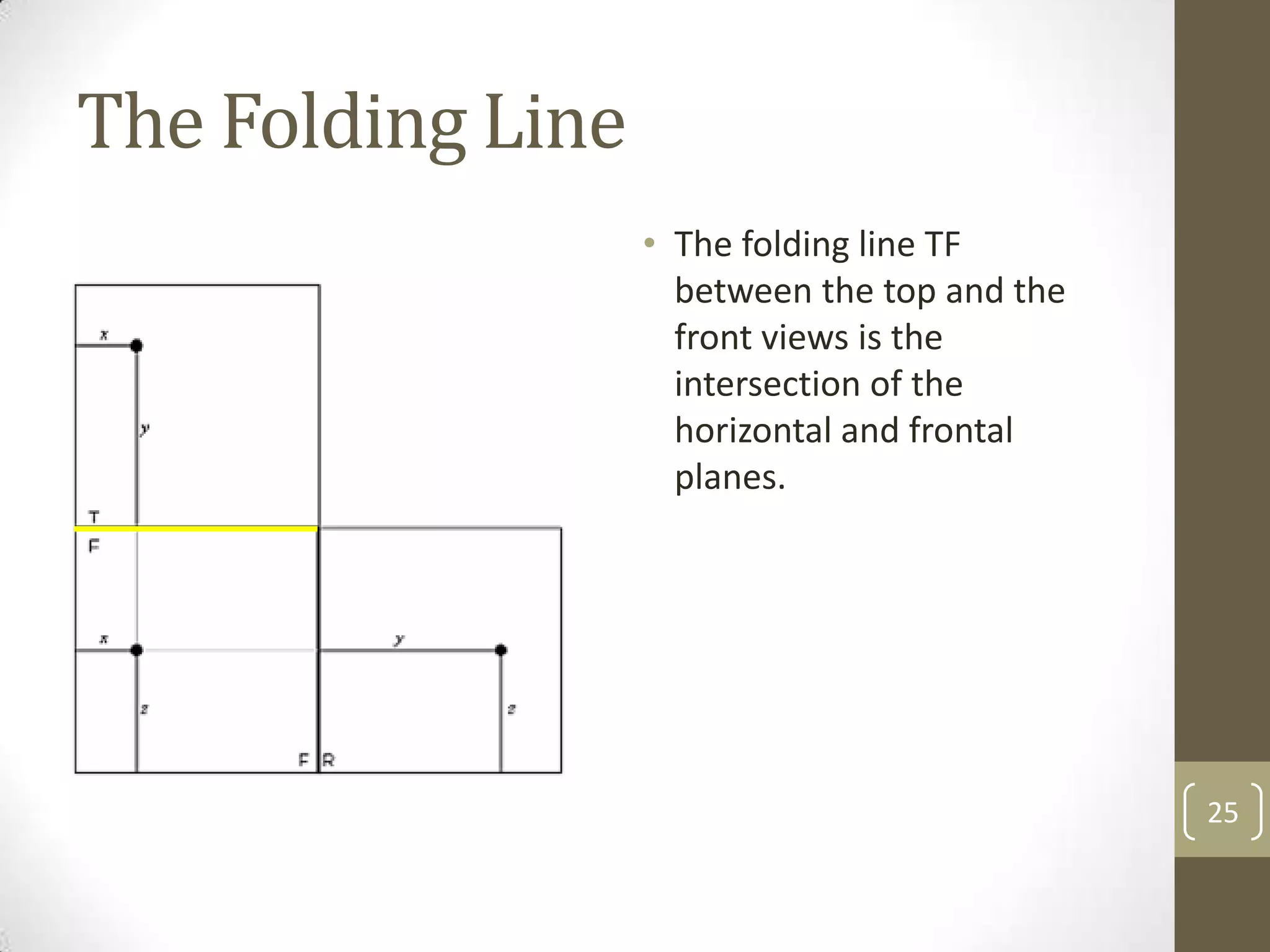
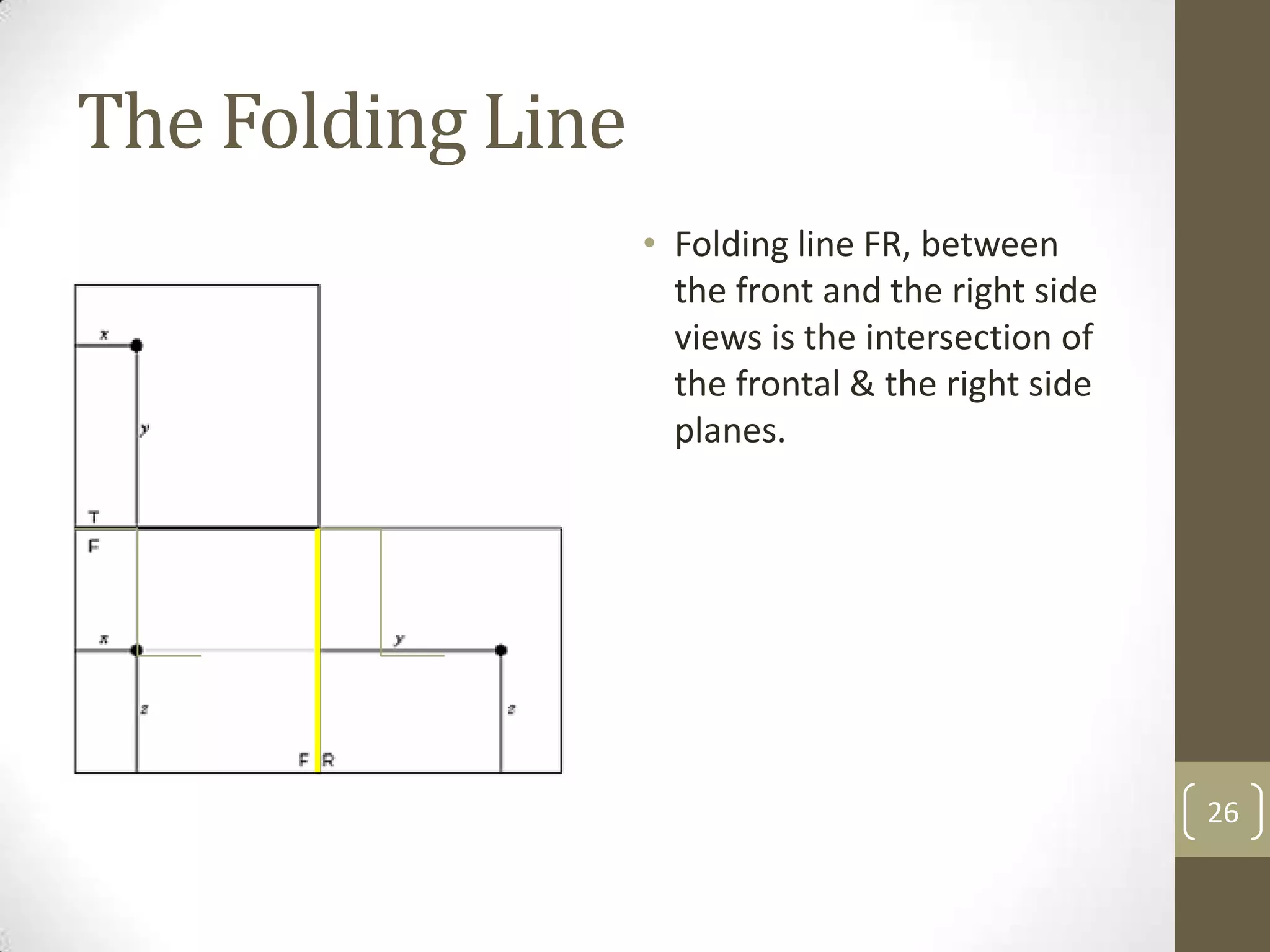
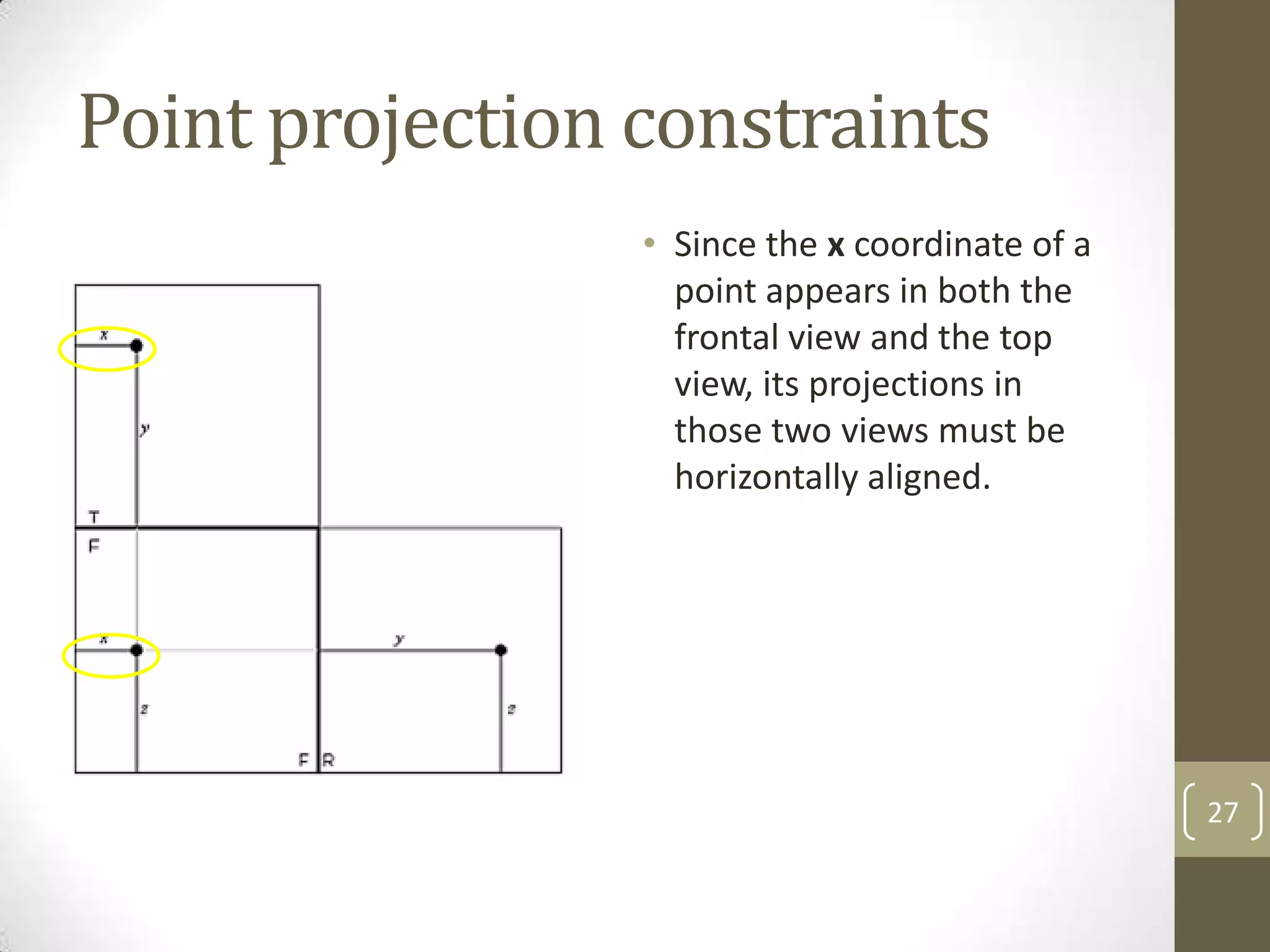
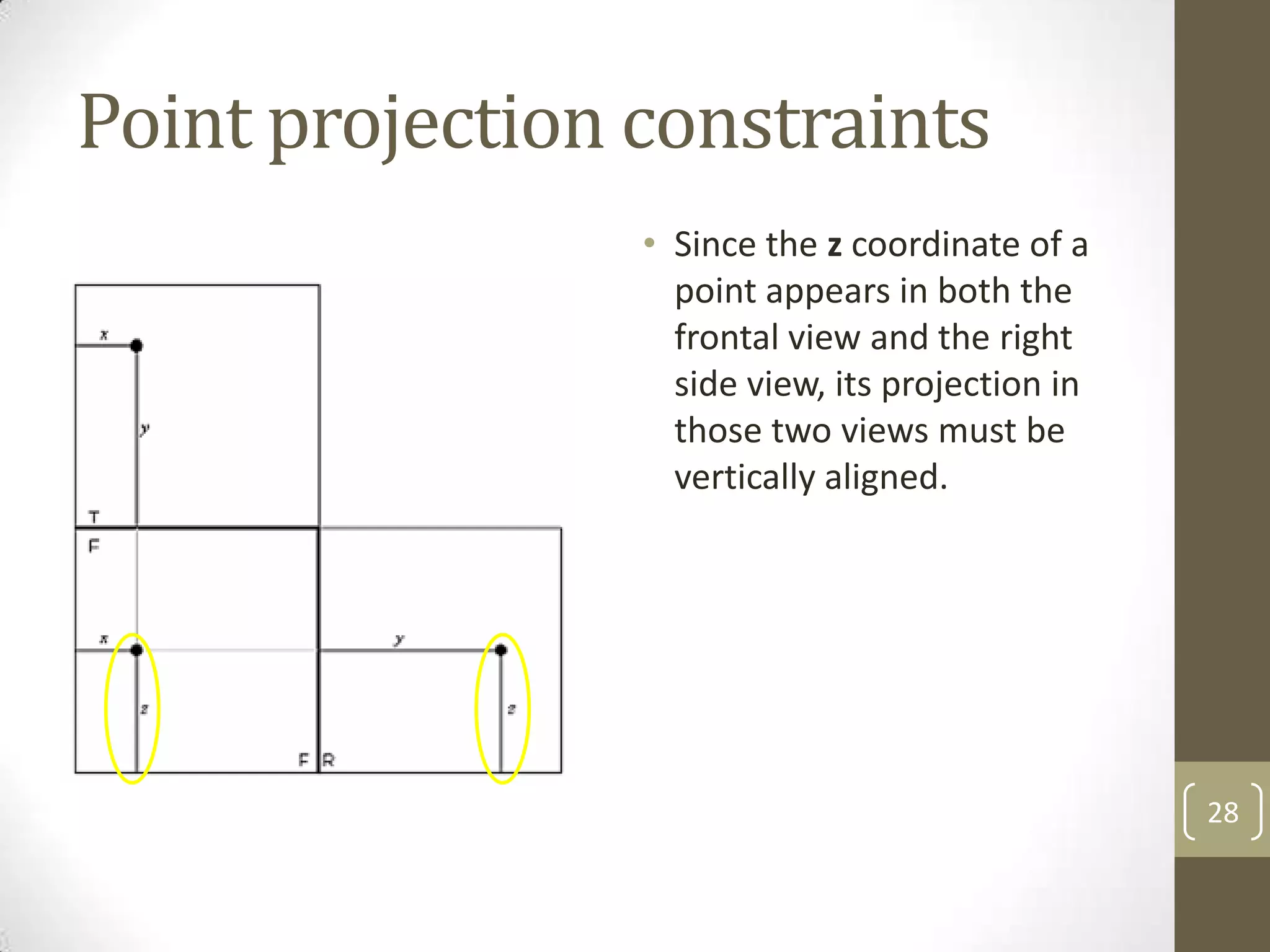
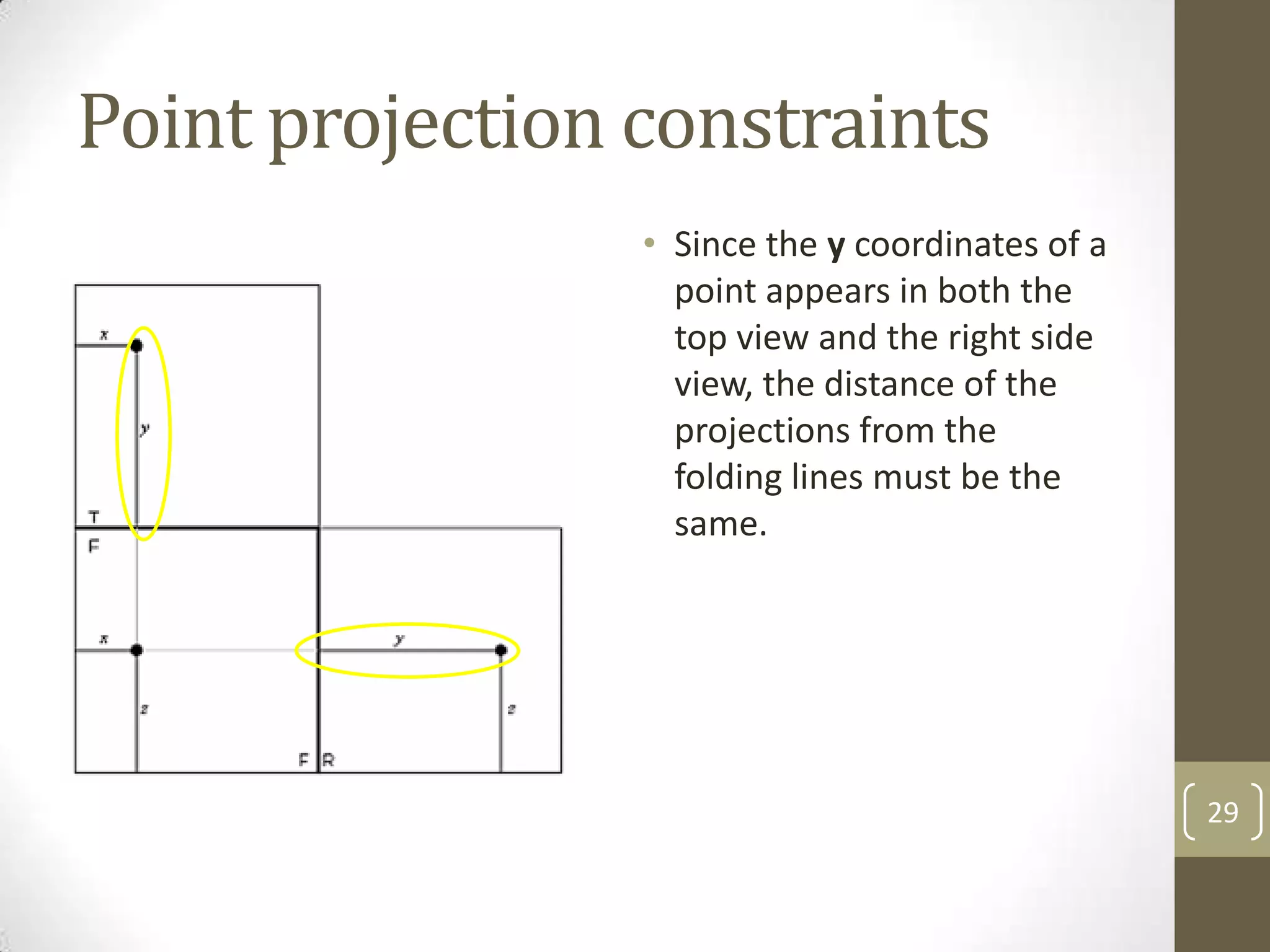
Descriptive geometry allows representing three-dimensional objects in two dimensions using specific procedures. Gaspard Monge developed these techniques in the 1700s. Orthographic projection projects points of an object perpendicularly onto planes of an imaginary glass box to form two-dimensional top, front, and side views. Principal planes are the box faces, while auxiliary planes can be any orientation. Projecting points defines their locations by coordinates in each view, with alignments across views following specific rules.

1. Descriptive
Geometry
ARCHT. TROY ELIZAGA
1

2. Descriptive Geometry
• Descriptive geometry the branch of geometry which allows
the representation of three-dimensional objects in two
dimensions, by using a specific set of procedures.
2

3. Descriptive Geometry
• Gaspard Monge is usually
considered the "father of
descriptive geometry".
• He first developed his
techniques to solve
geometric problems in
1765 while working as a
draftsman for military
fortifications, and later
published his findings
3

4. ORTHOGRAPHIC PROJECTION 4

5. Orthographic Projection
• Orthographic projection (or orthogonal projection) is a
means of representing a three-dimensional object in two
dimensions.
• It is a form of parallel projection, where all the projection lines
are orthogonal to the projection plane.
5

6. Orthographic Box
• Space is defined as the infinite extension of the three
dimensional region in which all matter exists.
• In order to study an object in space, it is necessary to
“enclose” the object so that we can make use of the enclosure
as a reference point.
• This is done with the use of the orthographic box.
6

7. Orthographic Box
• An orthographic box is an
imaginary glass box that
encloses the object in
space being studied.
7

8. Orthographic Box
• The sides of the box are
called planes of projection.
• By projecting the points of
the object perpendicularly
to the planes of projection
we are able to form an
IMAGE of the object
8

9. Orthographic Box
• Depending on their
position relative to the
person viewing the
orthographic box, the
images are called either
TOP VIEW image, FRONT
VIEW image, or SIDE VIEW
image
9

10. PLANES OF PROJECTION 10

11. Planes of Projection
• There are two main types of planes of projection
• Principal planes of projection
• Auxiliary planes of projection
11

12. Principal Planes of Projections
• Principal planes of projection are the main “faces” of the
orthographic box.
• They are labelled depending on their relative position to the
viewer.
• There are basically three principal planes of projections:
• Frontal Plane
• Horizontal Plane
• Profile Plane
12

13. Frontal Plane
• The plane facing the viewer
is called the Frontal Plane
(or F-plane).
• This is where the front
view images are projected
13

14. Horizontal Plane
• The plane perpendicular to
but horizontal to the
viewer is the Horizontal
Plane (or H-plane).
• This is where the top view
images are projected.
14

15. Profile Plane
• The plane perpendicular to
but vertical to the viewer is
the Profile Plane (or P-
plane).
• This is where the side-view
images are projected
15

16. Alternatives
• It is also possible to project an image backwards, to the left,
and downwards to get the rear view, left side view, and the
bottom view respectively.
• In most problems, however, we normally consider its two
dimensional images in at least two views.
• Usually the top view and front view images will suffice.
• Following the American system for technical drawings, the
right side view may be used when a side view is necessary.
16

17. Auxiliary Plane of Projection
• The auxiliary planes of projections are any planes which are
neither parallel to nor perpendicular to the viewer.
• Their orientation is arbitrary.
• Their labels are also arbitrary, i.e. they may use any letters
other than the letters used to label the principal planes of
projections
17

18. The Auxiliary Plane
• In this figure, the object
has an inclined surface that
does not appear in its true
size and shape in any
regular view. The auxiliary
plane is assumed parallel
to the inclined surface P
18

19. The Auxiliary Plane
• The auxiliary plane is then
perpendicular to the
frontal plane of projection
and is hinged to it. The
inclined surface is shown in
its true size & shape in the
auxiliary view. The long
dimension of the surface is
projected directly from the
front view and the depth
from the top view
19

20. PROJECTING POINTS 20

21. Points in space
• A point is a theoretical
location in space having no
dimension. A point in space
may be defined by its
coordinates from a fixed
reference.
• P = (x,y,z).
21

22. Projection of a point
• Given a point P = (x,y,z),
projecting P into the planes
of the glass box shows its x
and z coordinates in the
front plane, its x and y
coordinates in the top
plane and its y and z
coordinates in the profile
plane.
22

23. Projection of a point
• Unfolding the glass box
provides a complete
description of the point’s
location in the 3D space.
23

24. The Folding Line
• The folding line is the
intersection between two
projection planes
24

25. The Folding Line
• The folding line TF
between the top and the
front views is the
intersection of the
horizontal and frontal
planes.
25

26. The Folding Line
• Folding line FR, between
the front and the right side
views is the intersection of
the frontal & the right side
planes.
26

27. Point projection constraints
• Since the x coordinate of a
point appears in both the
frontal view and the top
view, its projections in
those two views must be
horizontally aligned.
27

28. Point projection constraints
• Since the z coordinate of a
point appears in both the
frontal view and the right
side view, its projection in
those two views must be
vertically aligned.
28

29. Point projection constraints
• Since the y coordinates of a
point appears in both the
top view and the right side
view, the distance of the
projections from the
folding lines must be the
same.
29

30. Rule 1: The alignment rule
• The projections of a point
in two consecutive views
are aligned with respect to
the normal to the folding
line.
30