The document discusses the Bertrand model of competition, focusing on price rivalry between two firms producing differentiated goods with different costs. It outlines various equations related to production levels, utility, and strategies for price and cost delegation games within this model. Key features and lemmas related to firm behavior in shifting between price modes are also analyzed.

1. PM/RM Concept in Bertrand
Model
Algorithm – Project 1
Kavi Pandya
Roll- 131020
SEM-5
04-09-2015

2. Understanding Bertrand
Cournot Model
• Firms compete in quantities
• Ex:
Bertrand Model
• Firms compete in prices
• Ex:
Quantity: 1.2 lakh 1.1 lakh Price: Rs. 110 Rs. 92
Features Of Bertrand Model :
1. There are only two firms in the market.
2. They are producing differentiated goods.
3. Both the firms have different production cost.
4. Firms have control over their product's price and cost.

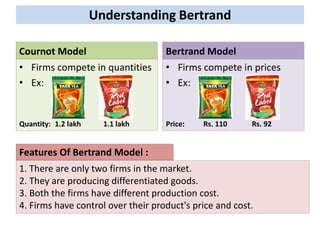
3. PM/RM in Bertrand
Equations:
Production Level(xi) for two firms are:
1st firm : x1 = a - b1*p1 + b2*p2
2nd firm : x2 = a - b1*p2 + b2*p1
Utility(Ui) of firms:
PM : Ui = (pi - ci)*xi
RM : Ui = pi*xi
pi = Price,
ci = Production Cost
bi = +ve constants
LEMMA’s :
4. If both the firms are in PM, then
If the Higher-price firm switches to RM then the lower-price firm should also switch
to RM.
1. If a firm switches from RM to PM then its price increases
2. If a firm switches from PM to RM then it is in capacity to reduce its price to
certain extent and the minimum price is given by:
p1rm = [(a + b2*p2)/(2*b1)] - [(( ((a + b2*p2)/b1)^2 - 4*(p1pm - c1pm)(a -
b1*p1pm + b2*p2)/b1 )^1/2)/2]
3. If both the firms are in RM, then
(i). If lower-price firm switches to PM then the higher-price firm should stick to RM
(ii). If higher-price firm switches to PM then the lower-price firm should also switch
to PM.

4. Cost Delegation Game in Bertrand
STEP-1 : Agents determine price:
Firm 1: dU1/dp1 = 0, gives: p1 = (a + b2*p2 + c1*b1)/(2*b1)
Firm 2: dU2/dp2 = 0, gives: p2 = (a + b2*p1 + c2*b1)/(2*b1)
STEP-2 : Owners determine cost:
Firm 1: dU1/dc1 = 0, gives: c1 = (a + b2*p2)/(b1)
Firm 2: dU2/dc2 = 0, gives: c2 = (a + b2*p1)/(b1)
Equations: Utility(Ui) of firms:
Ui = (pi - ci)*xi
Production Level(xi) for two firms are:
1st firm : x1 = a - b1*p1 + b2*p2
2nd firm : x2 = a - b1*p2 + b2*p1
Utility(Ui) of firms:
U1 = (p1 - c1)*(a - b1*p1 + b2*p2)
U2 = (p2 - c2)*(a - b1*p2 + b2*p1)

5. Overview : Project-1
1. Understanding Bertrand Model
2. PM/RM Delegation Game in Bertrand Model + 4 Lemmas
3. Generalized Cost Delegation Game in Bertrand Model
THANKS