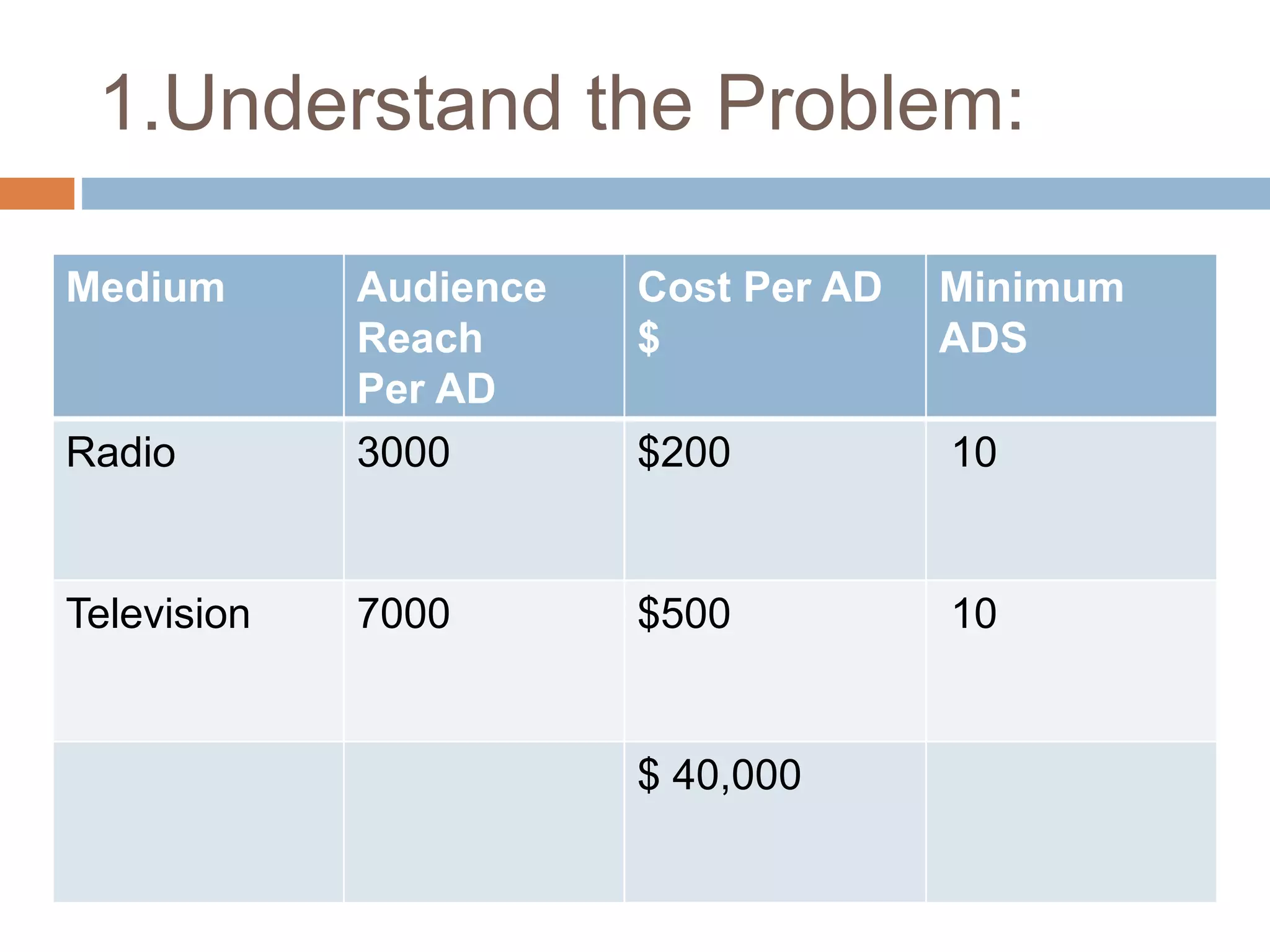
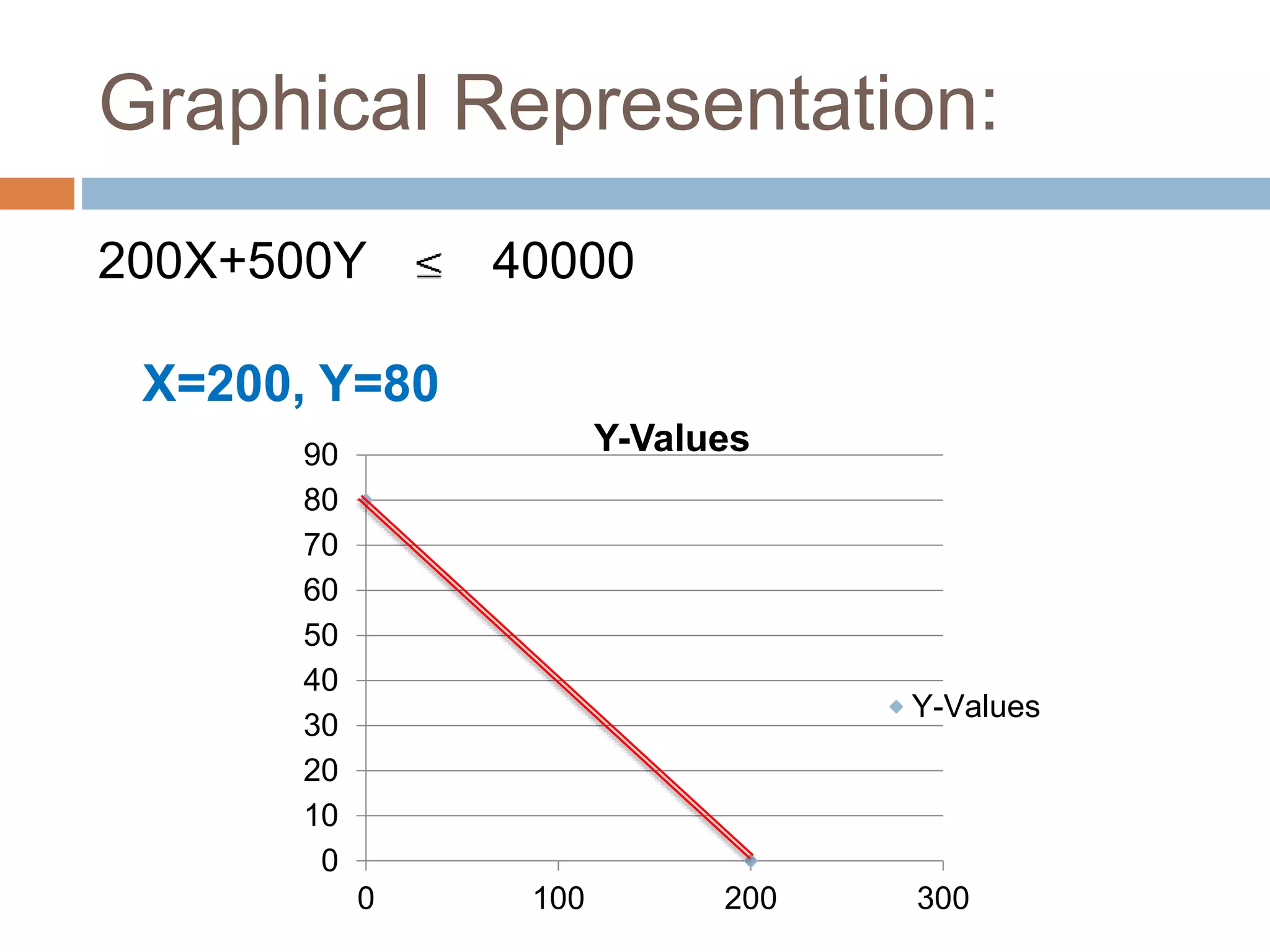
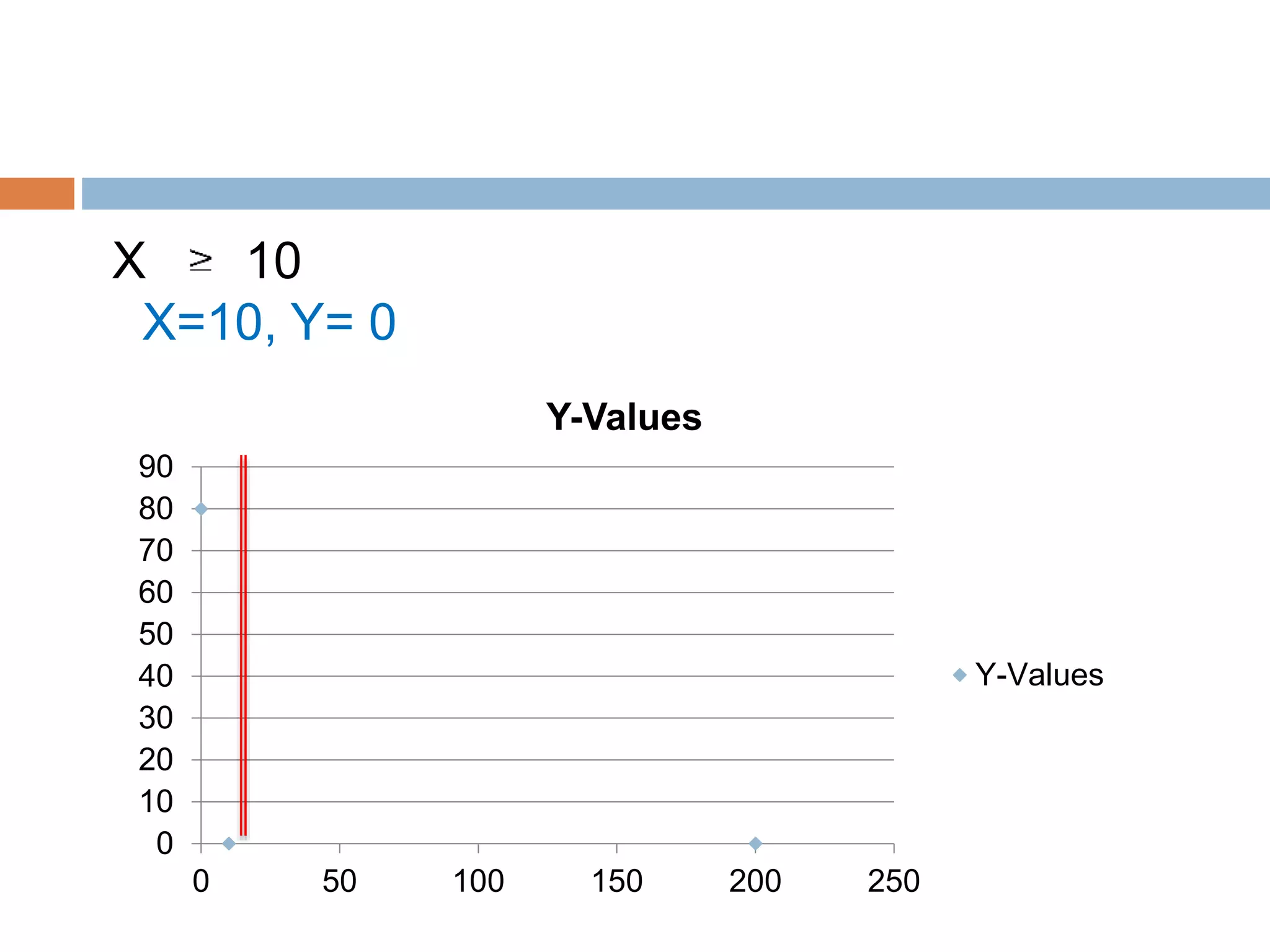
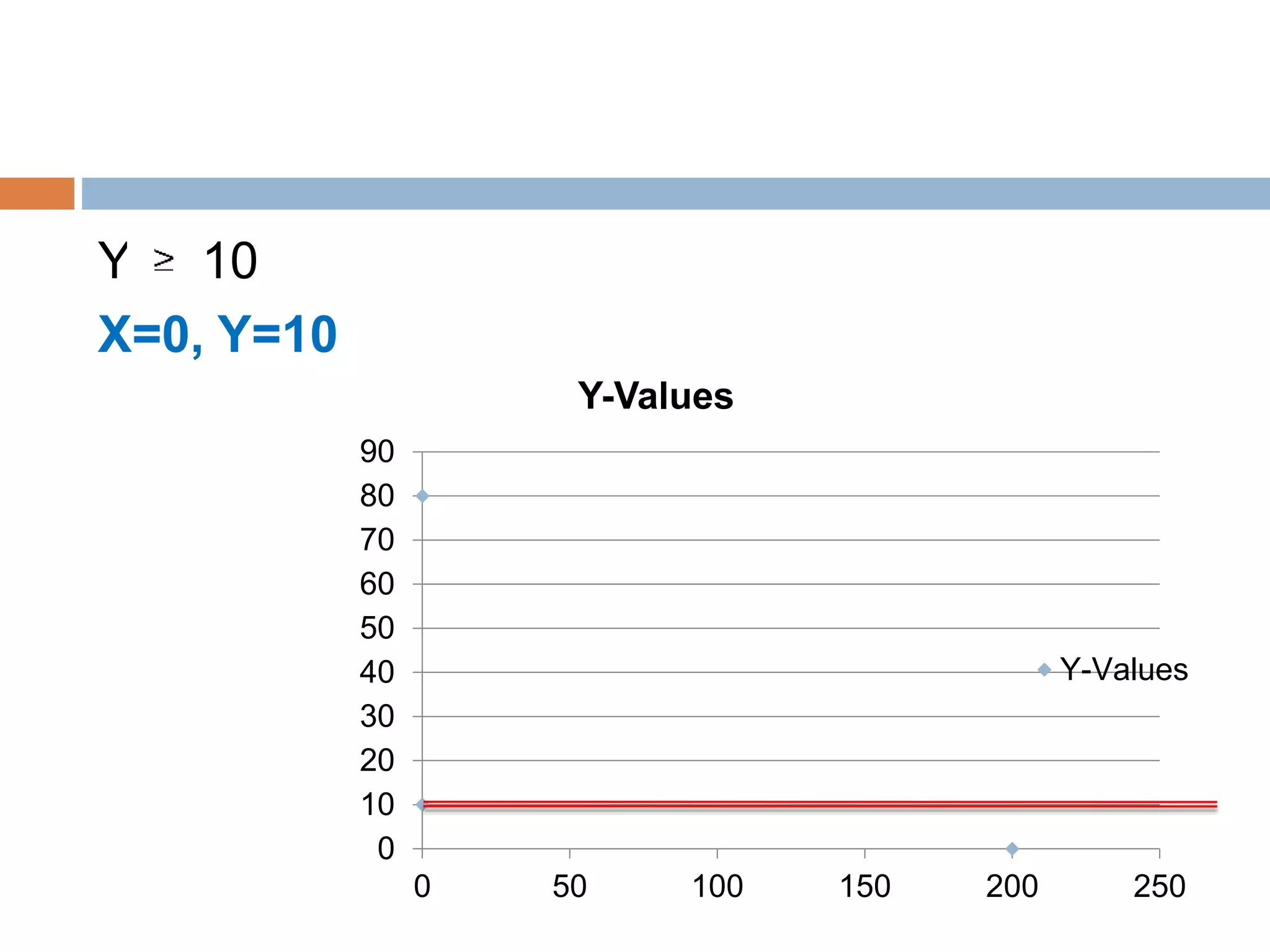
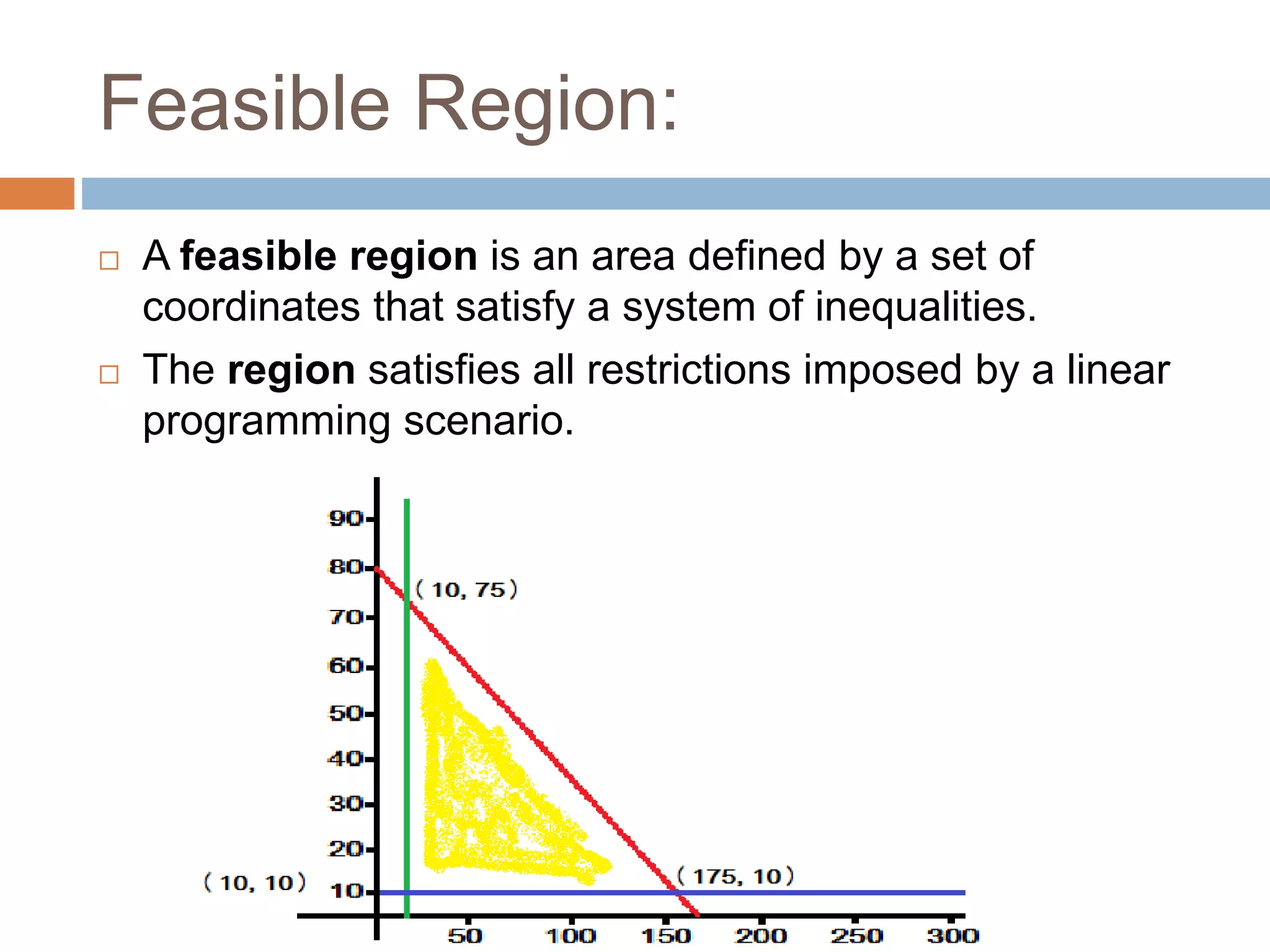
This document discusses linear programming and its application to marketing. It covers topics like the requirements, methods, advantages/disadvantages of linear programming. It also provides steps to formulate a linear programming problem, including understanding the problem, identifying the objective and constraints, defining decision variables, and writing the mathematical model. Finally, it formulates an example problem to maximize advertisement reach within a budget, finds the optimal solution is 175 radio ads and 10 TV ads reaching 595,000 people.

2. LINEAR PROGRAMMING
MARKETING APPLICATION
Presented By:
Huma Rashid

3. Topics to be Covered:
 Introduction to Linear Programming
 Requirements
 Methods
 Linear Programming Application
 Formulation of Linear Programming Problem
 Drawbacks

4. Linear Programming
 Linear Programming is a technique that helps
in recourse allocation decision.
 It is a mathematical tool or technique for
efficient or effective utilization of “limited
resources” to achieve organization objectives
(maximization or minimization)

5. Requirements
 One Objective Function
 One or more Constraints
 Alternative Courses of Action
 Objective function and Constraints are linear
 Sources must be Limited
 Non-negative Variable

6. Methods
 Graphical Method
 Corner solution method
 Level curve method
 Simplex Method
 Dual Simplex Method

7. Advantages & Disadvantages
Advantages of Linear Programming:
 The main advantage of linear programming is its simplicity and easy way of
understanding.
 Linear programming makes optimal use of available resources
 Linear programming is adaptive and more flexibility to analyze the problems.
 The better quality of decision is provided.
Disadvantage of Linear Programming:
 Linear programming works only with the variables that are linear.
 It deals with the problem having single Objective
 Non linear function cannot be solved over here.
 Impossibility of solving some problem which has more than two variables in
graphical method.

13. Steps for Formulation of Linear
Programming
 Understand the managerial problem being
faced
 Identify the objective and constraint
 Define the Decision Variables
 Use Decision Variables to write Mathematical
Expressions for Objective Function and The
constrains

14. Formulation Of LP Problem
 A candidate for mayor in a small town has allocated $40,000
for last-minute advertising in the days preceding the election.
 Two types of ads will be used: radio and television. Each
radio ad costs $200 and reaches an estimated 3,000 people.
Each television ad costs $500 and reaches an estimated
7,000 people.
 In planning the advertising campaign, the campaign manager
would like to reach as many people as possible, but she has
stipulated that at least 10 ads of each type must be used.
 Also, the number of radio ads must be at least as great as
the number of television ads.
 How many ads of each type should be used?
 How many people will this reach?

15. 1.Understand the Problem:
Medium Audience
Reach
Per AD
Cost Per AD
$
Minimum
ADS
Radio 3000 $200 10
Television 7000 $500 10
$ 40,000

16. 2.Identify the Objective
 Objective is maximizing the audience reach to
the advertisement, or Reach as many people
as possible.
 The objective function becomes;
Max= 3000X+7000Y
 X= no. of ads on Radio
 Y= no. of Ads on Television

17. 3.Identify the Constraints
 Total spend (in terms of the decision variables) must be
40K.
200X+500Y 40,000
 The number of radio ads must be 10
X 10
 The number of TV ads must be 10
Y 10
 The number of radio ads must be number of TV
ads.
X Y
 Non negativity constraint
X,Y 0

18. 4. Defining Decision Variables
 X= no. of ads on Radio
 Y= no. of Ads on Television
Equation 1:
200X+500Y=40,000
If X = 0, Y = 8
Y = 0, X=200
Equation 2:
X=10
Equation 3:
Y=10

19. Graphical Representation:
200X+500Y 40000
X=200, Y=80
0
10
20
30
40
50
60
70
80
90
0 100 200 300
Y-Values
Y-Values

20. X 10
X=10, Y= 0
0
10
20
30
40
50
60
70
80
90
0 50 100 150 200 250
Y-Values
Y-Values

21. Y 10
X=0, Y=10
0
10
20
30
40
50
60
70
80
90
0 50 100 150 200 250
Y-Values
Y-Values

22. Feasible Region:
 A feasible region is an area defined by a set of
coordinates that satisfy a system of inequalities.
 The region satisfies all restrictions imposed by a linear
programming scenario.

23. Optimal Solution:

Optimal Point is where X=175, Y=10
595000 PEOPLE will reach this AD
Constraint Points Audience Reach
( 10,10) 100000 people
(175, 10) 595000 people
(10, 75) 555000 people

24. Advertising Plan
Media Ads Budget $
Radio 175 35000
Television 10 5000
total 40000
Cost Function; 200X+500Y =40000
200(175) + 500(10) =40000