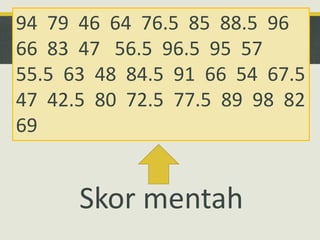
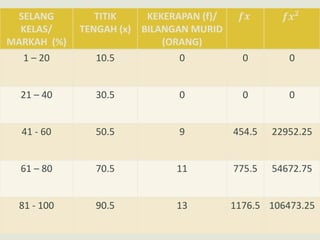
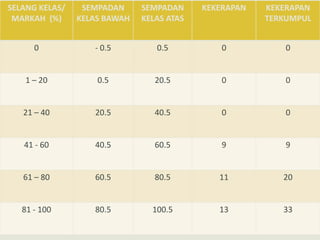
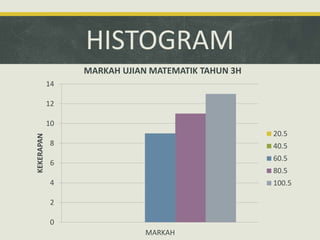
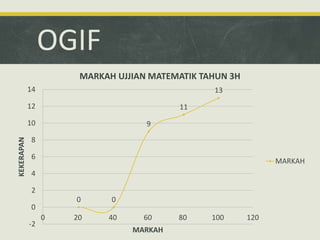
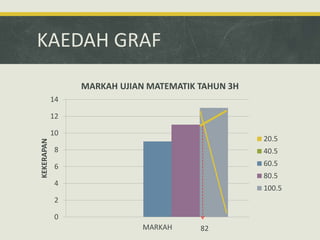
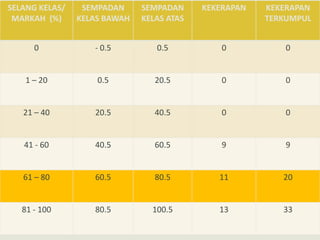
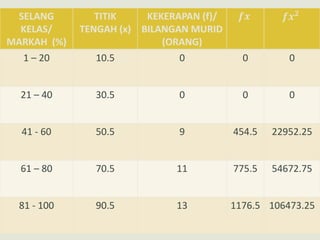
Dokumen ini mengupas sejarah dan konsep asas statistik, termasuk pengumpulan data dan analisisnya dalam konteks pemerintahan dan pendidikan. Ia membahas dua jenis statistik: deskriptif dan inferens, serta metode pengolahan data seperti pengiraan min, mod, dan median. Tambahan pula, analisis data pelajar dalam ujian matematik dimasukkan untuk menunjukkan pencapaian dan faktor penyebab kejayaan mereka.

1. STATISTIK ASAS

2. SEJARAH
PENGGUNAAN STATISTIK

3.  Berasal dari perkataan Latin state yang bermaksud
negeri atau negara
 Penggunaan awal statistik
 Melibatkan pengumpulan data atau maklumat yang
menerangkan beberapa aspek berkaitan dengan
sesebuah negeri atau negara semenjak zaman
Mesir, Greek dan Rom
 Memudahkan pengutipan cukai dan kerahan tenaga
 Menimbulkan minat kerajaan-kerajaan Eropah
Barat dengan penggunaan data statistik kerana
bimbang kuasa politik dan tentera tergugat
 Mengumpul data kelahiran, perkahwinan dan
kematian untuk memastikan perubahan saiz
penduduk

4. Captain John Grant menerbitkan semula data
mengenai kelahiran dan kematian yang
disebabkan oleh penyakit-penyakit tertentu
pada tahun 1662.
Kajian-kajian lain seperti
 Kadar kelahiran mengikut jantina
 Saiz penduduk
Pihak kerajaan, peniaga mahupun individu
amat bergantung kepada data statistik
sebagai panduan

5. PENGENALAN KEPADA STATISTIK
Statistik asas merupakan satu teknik
matematik memproses, menyusun,
menganalisis dan membuat kesimpulan
tentang data yang berbentuk kuantitatif

6. LANGKAH-LANGKAH DALAM STATISTIK
MENGUMPUL
MEMPROSES
MENGANALISIS
MENGINTERPRETASIKAN
MEMPERSEMBAHKAN

7. Statistik dibahagi kepada dua jenis,
iaitu:
Statistik perihalan
( statistik deskriptif)
Statistik inferens
( statistik induktif)

8. STATISTIK PERIHALAN
( STATISTIK DESKRIPTIF)

9. kaedah-kaedah yang digunakan untuk
megumpul maklumat, menyusun,
mempersembah data dan pengolahan
data/merihalkan data yang dikumpul
termasuklah kaedah membina graf, carta dan
jadual serta pengiraan beberapa ukuran
perihalan seperti purata dan juga pengiraan
ukuran serakan seperti peratus

10. STATISTIK INFERENS
( STATISTIK INDUKTIF)

11. merupakan bahagian terpenting daripada
statistik yang berkaitan dengan pembuatan
kesimpulan dan keputusan berdasarkan data
yang telah dikumpul dan diolah
Tumpuan utama dalam statistik inferens ialah
untuk mengetahui sesuatu keseluruhan ahli
kumpulan (populasi) berdasarkan sebahagian
yang dipilih (sampel) untuk dikaji

12. MARKAH UJIAN
MATEMATIK
KELAS 3 HIJAU
JUMLAH
PELAJAR : 33

13. 94 79 46 64 76.5 85 88.5 96
66 83 47 56.5 96.5 95 57
55.5 63 48 84.5 91 66 54 67.5
47 42.5 80 72.5 77.5 89 98 82
69
Skor mentah

14. MENYUSUN SKOR SECARA MENDATAR
DAN MENAIK
42.5 46 47 47 48 54 55.5 56.5
57 63 64 66 66 67.5 69 72.5
76.5 77.5 79 80 82 83 84.5 85
85.5 88.5 89 91 94 95 96 96.5
98

15. TABURAN KEKERAPAN
Kekerapan merujuk kepada berapa kali
sesuatu skor wujud dalam sesuatu taburan

16. SELANG
KELAS/
MARKAH (%)
TITIK
TENGAH (x)
KEKERAPAN (f)/
BILANGAN MURID
(ORANG)
𝒇𝒙 𝒇𝒙 𝟐
1 – 20 10.5 0 0 0
21 – 40 30.5 0 0 0
41 - 60 50.5 9 454.5 22952.25
61 – 80 70.5 11 775.5 54672.75
81 - 100 90.5 13 1176.5 106473.25

17. SELANG KELAS/
MARKAH (%)
SEMPADAN
KELAS BAWAH
SEMPADAN
KELAS ATAS
KEKERAPAN KEKERAPAN
TERKUMPUL
0 - 0.5 0.5 0 0
1 – 20 0.5 20.5 0 0
21 – 40 20.5 40.5 0 0
41 - 60 40.5 60.5 9 9
61 – 80 60.5 80.5 11 20
81 - 100 80.5 100.5 13 33

18. HISTOGRAM
0
2
4
6
8
10
12
14
MARKAH
KEKERAPAN
MARKAH UJIAN MATEMATIK TAHUN 3H
20.5
40.5
60.5
80.5
100.5

19. OGIF
0 0
9
11
13
-2
0
2
4
6
8
10
12
14
0 20 40 60 80 100 120
KEKERAPAN
MARKAH
MARKAH UJJIAN MATEMATIK TAHUN 3H
MARKAH

20. ANALISIS DATA

21. SUKATAN KECENDERUNGAN
MEMUSAT
Min
Mod
Median

22. MIN
Σ𝑓𝑥
Σ𝑓

23. MIN
Σ𝑓𝑥
Σ𝑓
=
2406.5
33
= 72.92
• Menunjukkan purata markah yang diperoleh
• Menggambarkan prestasi keseluruhan untuk
tujuan memberbandingkan prestasi
• Berguna semasa mengira sisihan piawai dan
skor sisihan

24. MOD

25. MOD
Skor yang mempunyai kekerapan yang paling
tinggi dalam satu taburan
Modal kelas : ( 81 – 100) markah

26. KAEDAH GRAF
0
2
4
6
8
10
12
14
MARKAH
KEKERAPAN
MARKAH UJIAN MATEMATIK TAHUN 3H
20.5
40.5
60.5
80.5
100.5
82

27. MEDIAN

28. MEDIAN, m
𝑚 = 𝐿 +
𝑁
2
− 𝑓𝑝
𝑓𝑚
𝐶
𝐿 = had bawah jeda kelas median
𝑓𝑝 = jumlah terkumpul kekerapan sehingga kelas
tersebut tetapi tidak melibatkan kekerapan
median kelas
𝑓𝑚 = kekerapan median
𝐶 = keluasan jeda kelas median
ℎ𝑎𝑑 𝑎𝑡𝑎𝑠 𝑘𝑒𝑙𝑎𝑠 − ℎ𝑎𝑑 𝑏𝑎𝑤𝑎ℎ 𝑘𝑒𝑙𝑎𝑠
𝑁 = jumlah bilangan kekerapan

29. SELANG KELAS/
MARKAH (%)
SEMPADAN
KELAS BAWAH
SEMPADAN
KELAS ATAS
KEKERAPAN KEKERAPAN
TERKUMPUL
0 - 0.5 0.5 0 0
1 – 20 0.5 20.5 0 0
21 – 40 20.5 40.5 0 0
41 - 60 40.5 60.5 9 9
61 – 80 60.5 80.5 11 20
81 - 100 80.5 100.5 13 33

30. PENGIRAAN MEDIAN
Kelas median = ( 61 – 80 ) markah
𝐿 = 60.5
𝑓𝑝 = 9
𝑓𝑚 = 11
𝐶 = 20
𝑁 = 33
𝑚 = 60.5 +
33
2
− 9
11
20 = 74.14

31. SUKATAN SERAKAN

32. SUKATAN SERAKAN
Sisihan piawai
Varians

33. SISIHAN PIAWAI
𝜎 =
𝑓𝑥2
𝑓
−
𝑓𝑥
𝑓
2
𝑓𝑥
𝑓
adalah rumus bagi mencari min, 𝑚

34. VARIANS
𝜎2
=
𝑓𝑥2
𝑓
−
𝑓𝑥
𝑓
2

35. SELANG
KELAS/
MARKAH (%)
TITIK
TENGAH (x)
KEKERAPAN (f)/
BILANGAN MURID
(ORANG)
𝒇𝒙 𝒇𝒙 𝟐
1 – 20 10.5 0 0 0
21 – 40 30.5 0 0 0
41 - 60 50.5 9 454.5 22952.25
61 – 80 70.5 11 775.5 54672.75
81 - 100 90.5 13 1176.5 106473.25

36. PENGIRAAN VARIANS DAN SISIHAN PIAWAI
Σ𝑓 = 33
Σ𝑓𝑥 = 2406.5
Σ𝑓𝑥2
= 184 098.25
𝜎 =
184 098.25
33
−
2406.5
33
2
= 260.78
= 16.15
varians, 𝜎2
= 260.78

37. INFERENS DARIPADA
DATA YANG DIPEROLEHI

38.  Semua murid yang menduduki ujian matematik ini telah
lulus
 Kebanyakan mereka mendapat keputusan yang agak
cemerlang.
 Seramai 14 orang pelajar memperoleh markah yang
tinggi di antara 81-100 dan berada pada gred A

39. FAKTOR PENYEBAB
Kebanyakan murid dapat memahami dan
menguasai apa yang telah dinyatakan dalam
sukatan pelajaran yang telah diajar dalam kelas
Mereka telah memahirkan diri dengan
matematik dengan adanya latihan yang
secukupnya
Guru telah melaksanakan proses pengajarannya
dengan berjaya

40. CARA UNTUK MENGEKALKAN PRESTASI MURID
Memberikan latihan yang secukupnya selepas
pengajaran suatu topik
Guru berusaha menarik minat pelajar
terhadap proses pembelajarannya melalui
pengajaran yang kreatif bagi mengurangkan
kebosanan dan membantu menumpukan
perhatian

41. SEKIAN
TERIMA KASIH