1. This document discusses the history and development of deep learning from the perceptron in 1958 to modern deep neural networks. 2. It describes the key milestones as the perceptron in 1958, multilayer perceptrons in the 1980s which could solve the XOR problem, and Boltzmann machines in the 1980s which introduced unsupervised learning. 3. Deep learning has gained popularity since 2010 due to increases in data and computational power. It is now being applied to problems in computer vision, natural language processing and other domains.

1. %ìÝ(Deep Learning)X í¬@ ¬, ø¬à
ôtYX ©
@Ä-
2014D 10Ô 8|
” }
ü ‰X” 0ÄYµ(Machine Learning) )•x %ìÝ(Deep Learning)Ð t LDôà ôtY
X © ¥1Ð t Ðtøä.
1 `
0ÄYµ(Machine Learning)@ ôè0 ¤¤ YµXì !¨D X” xõÀ¥X „|tp,
%ìÝ(Deep Learning)@ xX à½ÝX Ь| t© ì5à½Ý(Deep Neural Network)t`D t©
0ÄYµ)•tä. %ìÝ 0 @ tø l, ˜t¤, DÈt ñ Œ IT0ÅäÐ ”XŒ t©
à ˆ” 0 tp ¹ˆ, (4xÝt˜ ¬Ä, L1 ñX xÝ, 0Ĉí ñX ð¸´˜¬(Natural Language
Processing)Ð ‹@ 1¥D X” ƒ L$8 ˆ”p, MIT 2013DD [¼ 10 à0 X˜
Xà ¸(Gartner, Inc.) 2014 8Ä IT Ü¥ 10 ü” !0 ¸ X” ñ ü ¥ (p´
tˆ à ˆä[34, 6]. %ìÝt 0tX µÄYt˜ äx 0ÄYµ )•ü äx p (t@ xX Ì|
0Xì $ÄÈä” tä. x@ ôè0 Dü ç@ ÜÐ ` ˆ” Ä°Ä }Œ t¼ Æ”
t, ôè0” xt }Œ xÀX” ¬Ät˜ L1D tXÀ »X”p t” xX Ì Ä­œ X
tðü ÜŤX Ñ,ð° tè´8 ˆ0 L8tä. X tð@ 0¥t ô˜ƒ ÆÀÌ Î@ tðät
õ¡XŒ ð°´ Ñ,ð°D ‰h ôè0 XÀ »X” L1, ÁxÝD ÔXŒ ` ˆ”
ƒtp %ìÝ@ t Î@ tðü ÜŤX Ñ,ð°D ôè0 ¬X” )•x ƒtä. tƒt Œ IT
0Åät %ìÝD ü©X” t | ƒtä. tÐ ø Д xõà½Ý t`X í¬€0 ¬ ÁiLÀ|
µˆ ¬ðt ü ƒtp t )•t õôtD ¥Áܤ”p ´»Œ t© ˆD ƒxÀ Ýt ôÄ]
X ä.
2 %ìÝX í¬
%ìÝX í¬” lŒ 3Ü0 ˜X´À”p 18” X x½àõÝx |I¸`(Perceptron), 28”
ä5(Multilayer) |I¸`, ø¬à ¬X %ìÝD 38|à ` ˆD ƒtä.
1

2. 2.1 18: Perceptron
xõà½Ý(Neural Network)X 0Ð@ 1958DÐ Rosenblatt H |I¸`t Ü‘t| ` ˆä[25].
nX inputü 1X outputÐ Xì X inputX weight| wi| Ä |I¸`D Ý ˜À´t
äLü ä(ø¼ 1)[14].
y = '(
Xn
i=1
wixi + b) (1)
(b: bias, ': activation function(e.g: logistic or tanh)
ø¼ 1: Concept of Perceptron
‰ nX inputX °i(Linear Combination)Ð Activation h| ©Xì 01 ¬tX U`
yD õX” ƒtp, U` @ ÄД ¸XÐ 0| 0| 0 eventÐ DÈÐ(1 VS -1)|
èä.
tƒt xõà½Ý ¨X Ü‘tä. Ș t ¨@ Dü è XOR problemÈ YµXÀ »X”
ñ, ì 8 ˆ”p(ø¼ 2) t L8Ð ÙH Æt ìXŒ ä[9].
2.2 28: Multilayer Perceptron
XORñ è ƒÄ YµXÀ »X” |I¸`X èD t°X0 )•@ Xx èX”p Input
layer@ output layer¬tÐ X˜ tÁX hidden layer| ”Xì YµX” ƒt øƒtp t| ä5 |I
¸`(Multilayer perceptron)t| ä. ø¼ 5| ôt hidden layer `] „X%t ‹DÀ” ƒD
Ux` ˆä. Ș t )•@ hidden layerX / `] weightX /Ä Ä XŒ
´ Yµ(Traning)t ´5ä” èt ˆ”p Rumelhartñ@ Ðìí

3. Lଘ(Error Backpropagation
Algorithm)D Xì ä5 |I¸`X YµD ¥XŒ Xä[26]. Ðìí

4. LଘX 8 …@
8à8Ìt˜ x07D Dô0 |p ì0” 0¥ 0x $…t ô ä.
2

5. ø¼ 2: XOR problem in Perceptron
: LÝX © Þ”0[9] à0(

6. sh) 2 ü(chip) 5, ©(ketchup) 3| l…t ©(price)
850ÐtÈät t| Ý äLü t ˜À¼ ˆp ø¼ 3Ð µˆ ¬ ´ ˆä.
price = xfishwfish + xchipswchips + xketchupwketchup (2)
ø¼ 3: Example: Weight Estimation
t L ©D ˜À´” vector w| w=(wfish;wchips;wketchup)ü t XXà error| 1
2 (t y)2
XXt(y: Estimation, t: Real), °¬X ©” ÐìD Œ X” w| ”X” ƒt ä. ä5|
I¸`Д ¨wi)äX / 4 ÎD ŒÀ„Ð ð” Œñ”É(Least Square Estimator),
¥Ä”É(Maximum Likelihood Estimator)| ø Æà, LଘD t©Xì ÐìX ŒÐ
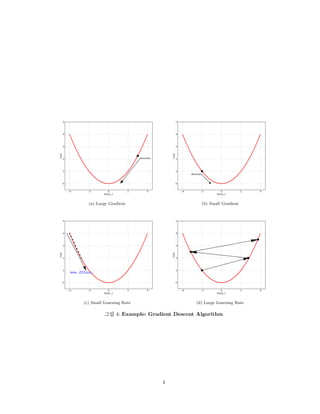
LÌÀŒ t| X”p ì0 t©” ƒt Gradient descent )•tä. t” ø„ÄÐ D@Xì ¨|
ä” ƒt ¹Õxp t| èˆ ¬Xt ø¼ 4 @ ä[8].
°¬ ÐX” Œ| L” €„ ø„Ä 0| LtÀ ø„Ä lt lŒ weight| Ôüà
ø„Ä ‘t ‘Œ Ôä” ƒtä. Learning rate| °` ˆ´ ¼È˜ lŒ ÀÀ
µx Ä| °` Ä ˆä.
t t| ©Xì | €´ô, 0 à0@ ü ©t ¨P 50Ðt|à Xt à0 2,
3

7. (a) Large Gradient (b) Small Gradient
(c) Small Learning Rate (d) Large Learning Rate
ø¼ 4: Example: Gradient Descent Algorithm
4

8. ø¼ 5: Multilayer Perceptron
ü 5, © 3X ´ ©@ 500Ðt ä. ¸ Ðìh| wiÐ t ø„Xt,
@E
@wi
=
@y
@wi
dE
dy
(3)
à E = 1
2 (t y)2, y = xfishwfish + xchipswchips + xketchupwketchupD …Xt
@E
@wi
=
@y
@wi
dE
dy
= xi(t y) (4)
à Learning rate| H wiX ÀTÉ@
wi =
@E
@wi
= xi(t y) (5)
t ä.
…tôt t=850, y=500, wfish = wchips = wketchup=50 tà è Ä°D t = 1
35 Xt
wfish=20, wchips=50, wchips=30t à t| ©Xt äÜ ltÄ weight” 70, 100, 80t
p t| ” ©@ 880t ä. t 880ü 850D Àà X üD č õXt 8Ð
L´ D »D ˆD ƒtä.
À $… ƒ@ ¥ 0x LଘD $… ƒtp ä $Xí

9. Lଘ@ 0 weight|
ä5 hidden layer| pÐ X˜X !D lXà ø !ü äX (t| í
weightäD t ˜Œ ä(ø¼ 6)[15].
Ðìí

10. Lଘ ä5|I¸`D Yµ` ˆŒ Ș tƒD ä ¬Œät t©X0Д
Î@ ´$Àt 0”p ø t ä@ äLü ä.
5

11. (a) Forward Propagation (b) Back Propagation
ø¼ 6: Backpropagation algorithm
1. Î@ Labeled data D”Xä.
2. YµD Xt `] 1¥t ¨´Ää(Vanishing gradient problem).
3. Over

12. tting problem
4. Local minimaÐ `È ¥1
X˜) ´´ô. ”t| X” ¨ Î0 L8Ð pt0 Ît D”Xà ø ÐÄ labeled data
Ît D”Xä. Ș °¬ à ˆ” pt0” unlabeled data è, Îp ä xX ÌX Yµ
Î@ €„t unlabeled data| t© Unsupervised Learningtp, @ ‘X labeled data ä5|I¸`
D YµXt …… hidden layer 1x ½°ôä 1¥t ¨´À” ½°| 0` ˆp tƒt üi
(Over

13. tting)X Ütä.
äL Activation functionD ´´ôt logistic functiontà tanh functiontà ´p €„ôä ‘ ]
t ˆ 0¸0X ÀT ‘@ ƒD ¬` ˆä(ø¼ 7). L8Ð Yµt ĉ ] Ä 0¸0D
0Ð LÌ8 ˜Ð” pX Gradient descent |´˜À JD Yµt À J” èt ˆä[2].
ÈÀÉ Œñ”Ét˜ ¥Ä”Éñ Á ŒD lX” )•D t©XÀ »X
à LଘD t©Xì ŒÐ LÌÀŒ ˆ0 L8Ð YµÐ ˜( Œt üð ÄÜ Œ(Global
minima)x? mŒ Œ(Local minima)” DÌ..Ð X8t €¬À JŒ ä. Ü‘D ´»Œ
PÐÐ 0| Local minimaÐ `È Ä ˆ0 L8tä (ø¼ 8)[15]. tð 8ä L8Ð ä Neural
Network@ ÀÀ¡08à(Support Vector Machine)ñÐ $ 2000D LÀ ©À »Xä.
2.3 38: Unsupervised Learning - Boltzmann Machine
^ ¸ èä L8Ð xõà½Ý t`t ˜ t©À »Xä, 2006D ü Ì 8àD t© Yµ)
•t ¬p…t xõà½Ý t`t äÜ YÄX ü©D Œ È”p t ü Ì 8àX uì Dt´”
Unsupervised Learning, ‰ labelt Æ” pt0 ø¬ ©„ YµD ä” ƒtp ø ÄÐ ^Ð ˜(
6

14. ø¼ 7: Sigmoid functions
ø¼ 8: Global and Local Minima
í

15. Lଘ ñD µt 0tX supervised learningD ‰ä[28, 12]. ø¼ 9Ð µx ¬
´ ˆ”p D0ä@ è´˜ L, 8¥X ;D ¨t” ÁÜ YµD Ü‘XŒ à LŒ(phoneme), è´
(word), 8¥(sentence) Unsupervised learningD ‰XŒ p ø ÄÐ õD Àà supervised
learningD ‰XŒ ä[15]. tð )•D µt ^ ¸ ä |I¸`X èät Ît t°”p,
Unlabeled data| t©` ˆà t| t©t unsupervised pre-trainingD ‰h vanishing gradient
problem, over

16. tting problemt ùõ ˆp, pre-trainingt ,x 0 ÐÄ ÄÀD ü´ local
minima problemÄ t°` ˆD ƒt| ì¨Àà ˆä[1]. tÐ ø Д ¥ x )•x Deep
Belief Network(DBN)ü t| ‰X0 t D” Restrict Boltzmann Machine(RBM)Ð Xì èˆ
$…X0 X ä.
7

17. ø¼ 9: Description of Unsupervised Learning
Restricted Boltzmann Machine(RBM) ü Ì 8à@ visible layer@ 1X hidden layer tè´Ä
)¥t Æ” ø˜(undirected graph) tè´8 ˆä. tƒX ¹Õ@ Energy based modelt|” xp
Energy based modelt|” ƒ@ ´¤ ÁÜ ˜, U`Ä h| ÐÀX Ü ˜À´ ä” ƒtp
visible unitX ¡0| v, hidden unitX ¡0| h| Xt(v,h: binary vector- 0 or 1) ü Ì 8àX ø˜@
U`Äh” äLü ä(ø¼ 10)[18, 19].
ø¼ 10: Diagram of a Restricted Boltzmann[32]
P(v; h) =
1
Z
expE(v;h) (6)
(Z: Normalized Constant)
ø¼ 10D ôt v|¬” t ð°´ ˆÀ Jà h|¬Ä È,Àxp tƒt RestrictedX Xøtp
t ptt Æt øå Boltmann Machinetp RBMÜX ø˜| t„ø˜(bipartite graph)| ä.
8

18. øå Boltzmann Machine@ 4 õ¡t Yµt ´$Ì ø H ˜( ƒt RBMx ƒtä. ¸ Ý
6| ôt ø˜X ÐÀ ÁÜ ®D] U`t ‘DÀ” ƒD L ˆ”p t @ ¬YX ôíY
2•YD ðÁܨä. t RBMX Energy functionD ´´ôt
E(v; h) =
X
i
aivi
X
j
bjhj
X
i
X
j
hjwi;jvi = aTv bTh hTWv (7)
(ai: oset of visible variable, bj : oset of hidden variable, wi;j : weight between vi and hj)
P
ÐÀÐ ÝÐ ì¨ ôD| ` €„t
j hjwi;jvixp, vi, hj 1x óÐ weight t] Ð
Àh t ‘DÀà °ü U`ÄhX t ’DÄä. t” xX ÜŤР|´˜” |ü
D·p, t À” ót ÜŤ ð° ¥1t ’0 L8tä(ø¼ 11).
ø¼ 11: Hebb's Law[21, 15]
t °¬ ÐX” ƒ@ P(v) =
P
h P(v; h) X D lX” ƒxp RBM@ t„ø˜ v|¬,
h|¬” € ŽtÀ
P(vjh) =
mY
i=1
P(vijh) (8a)
P(hjv) =
Yn
j=1
P(hj jv) (8b)
èˆ „¬` ˆp, tÐ 0x individual activation probabilities”
p(hj = 1jv) =
bj +
Xm
i=1
wi;jvi
!
(9a)
p(vi = 1jh) =
0
@ai +
Xn
j=1
wi;jhj
1
A (9b)
` ˆä(: activation function). t ¥D t©Xì Gibbs samplingD ðt weight| t
˜t èˆ logP(v)X ü øLX weightäD l` ˆ”p t )•Ð t µˆ LDô ä.
9