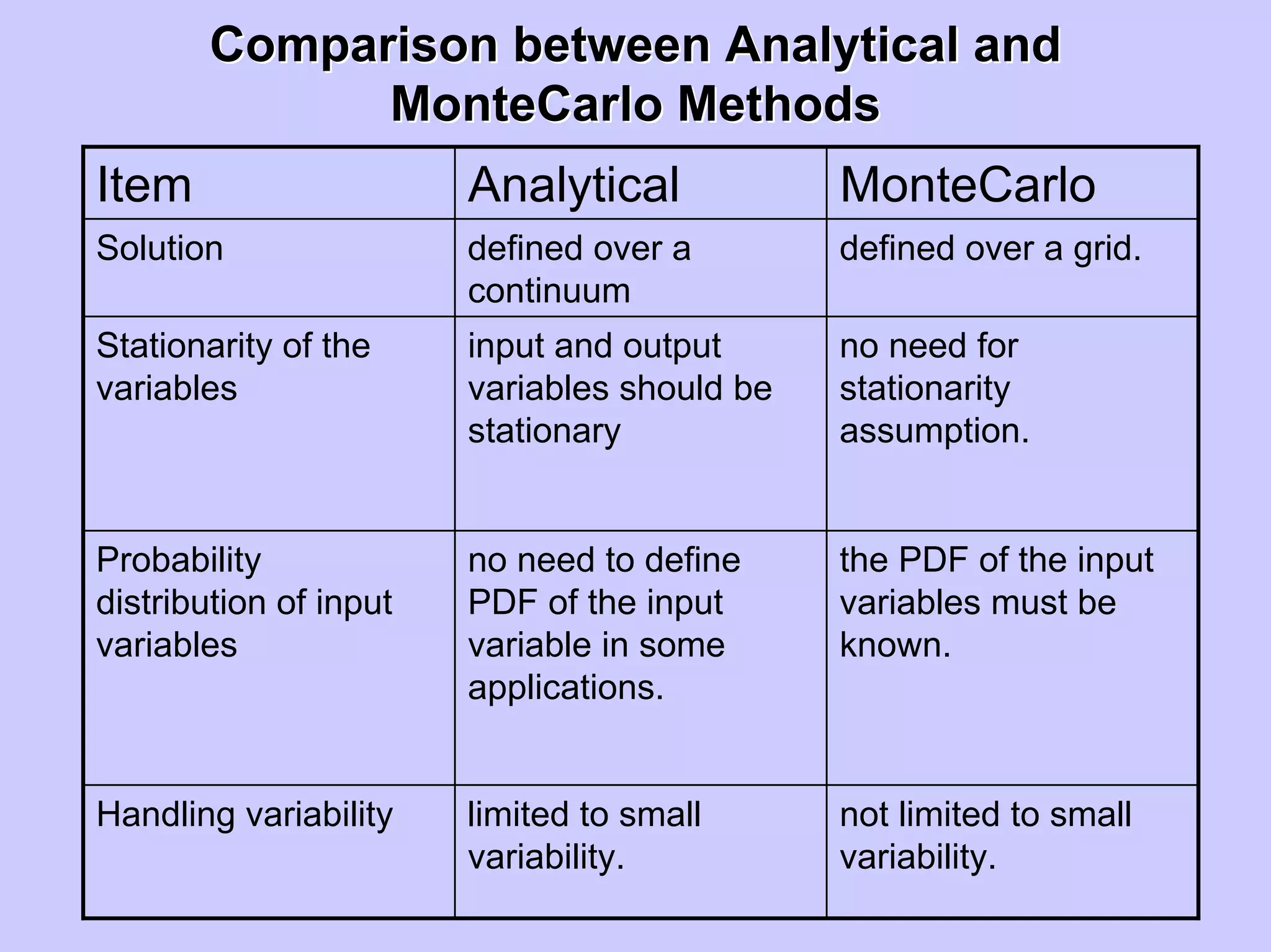
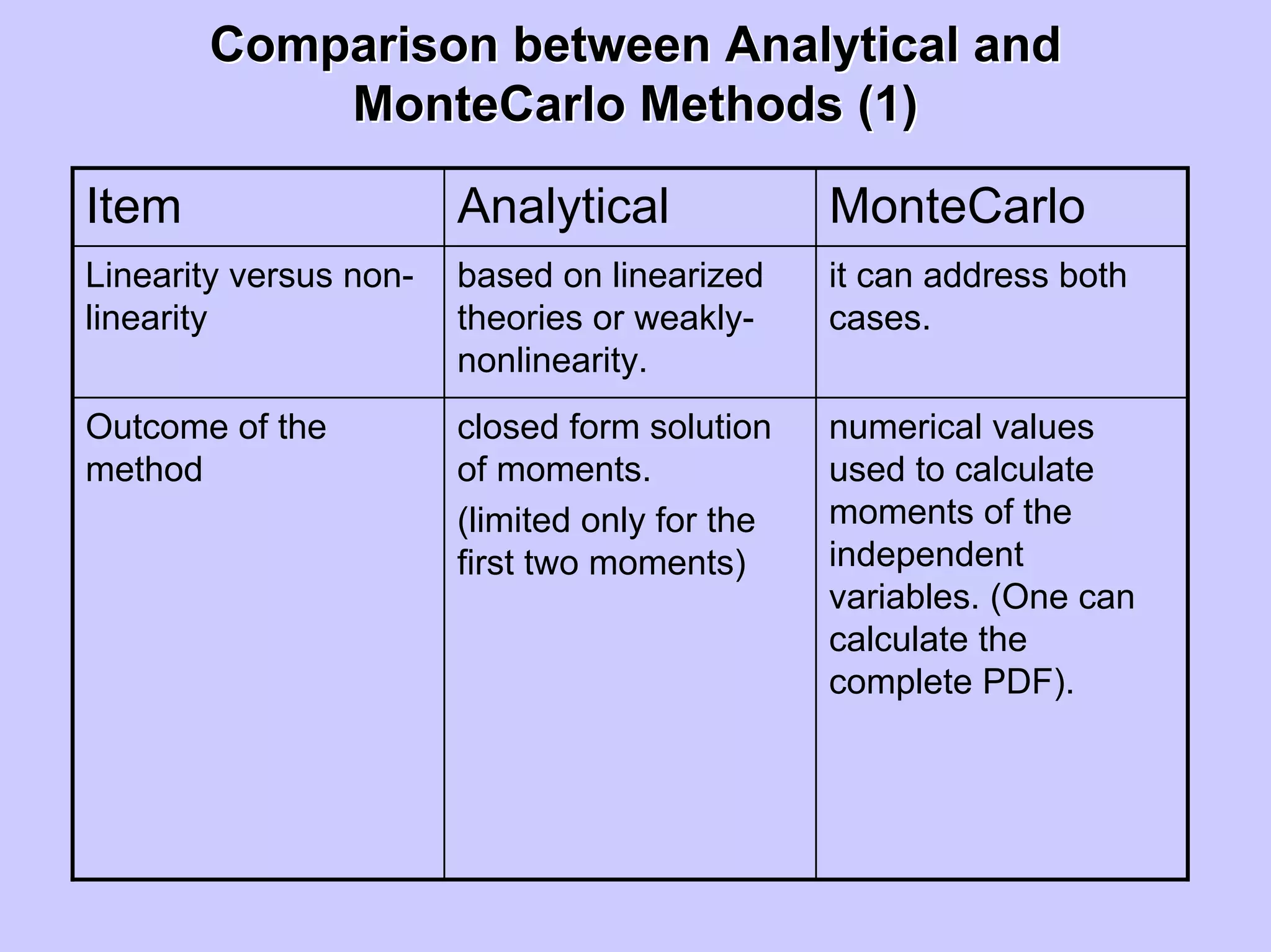
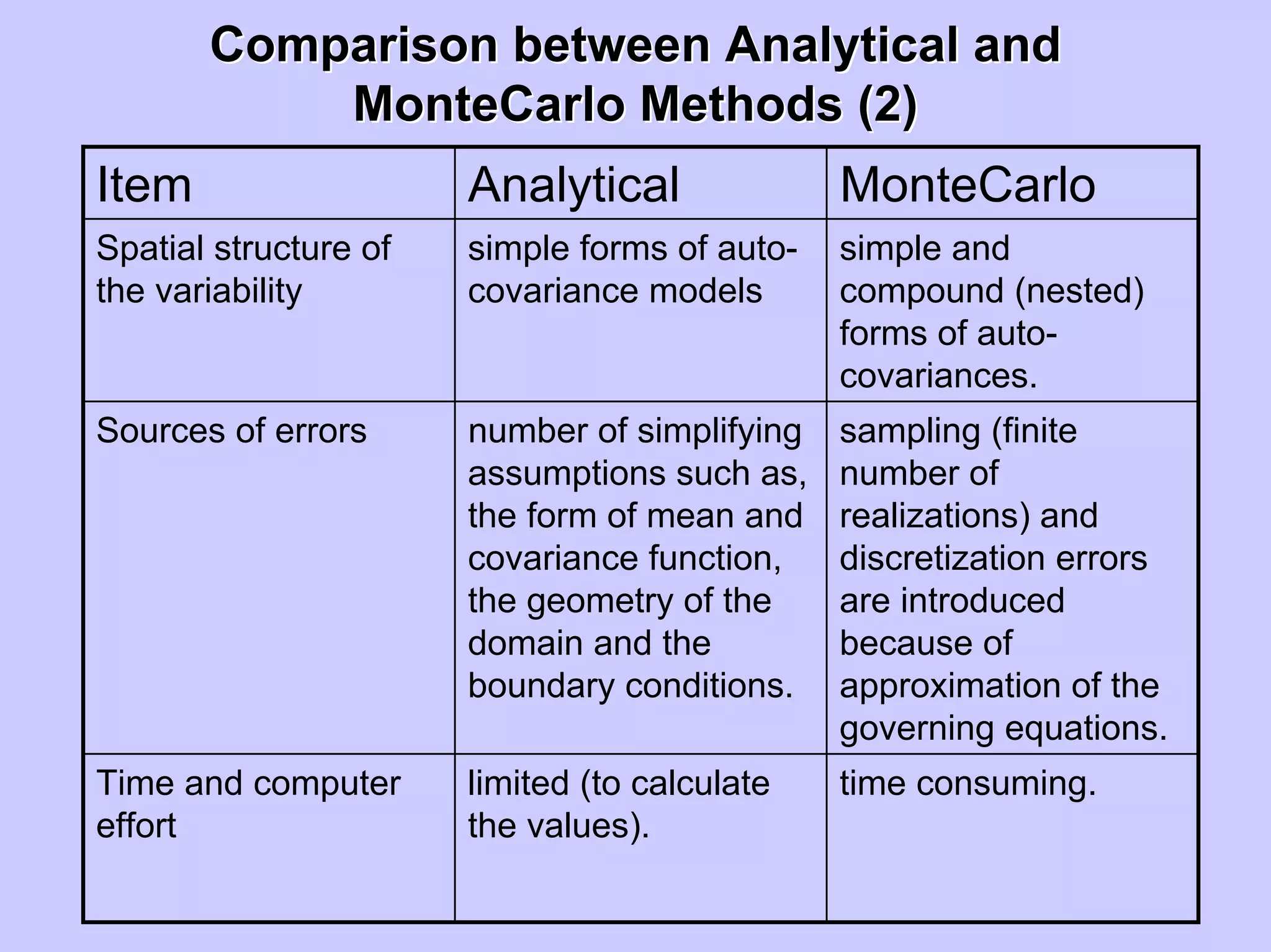
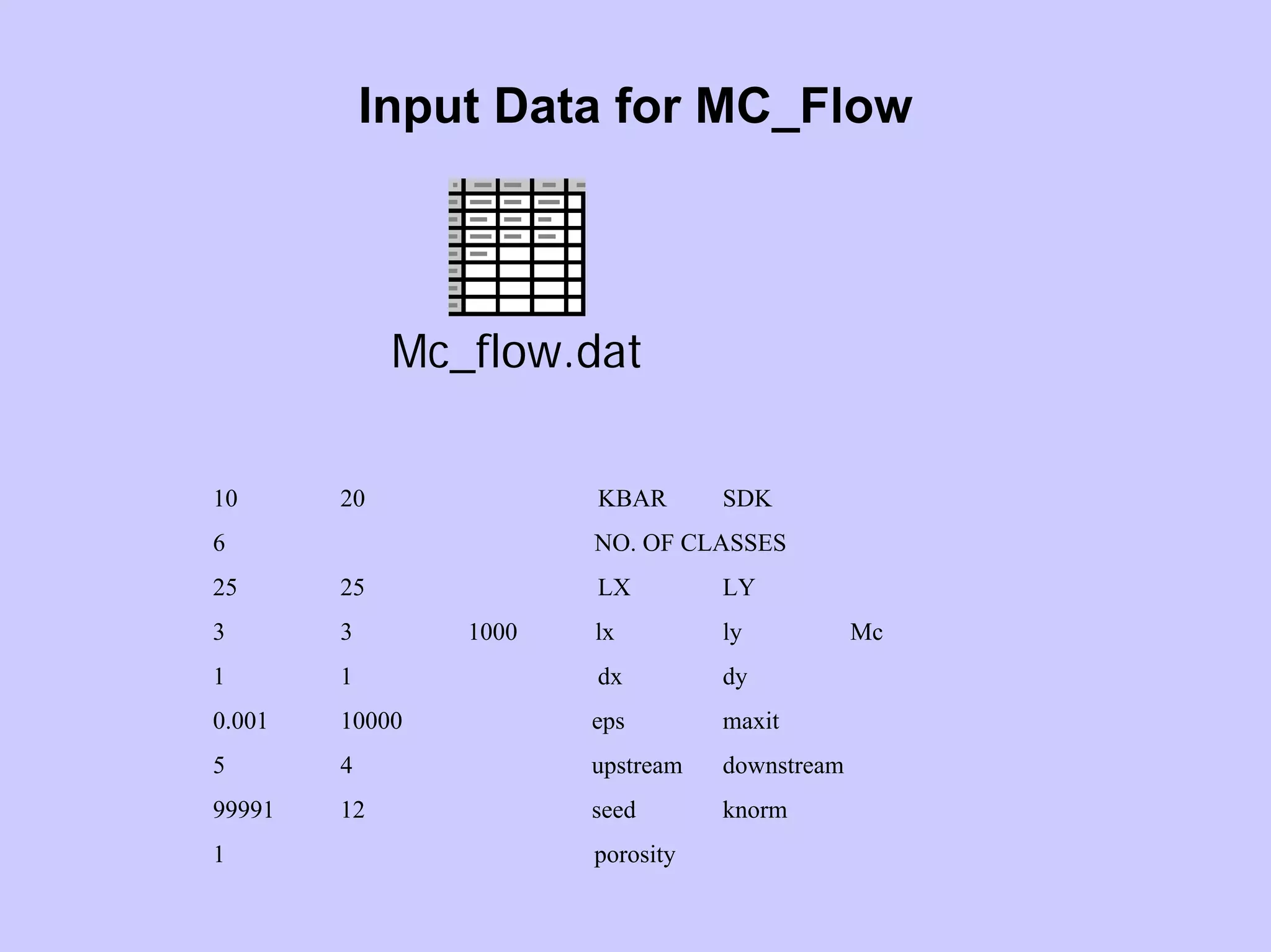
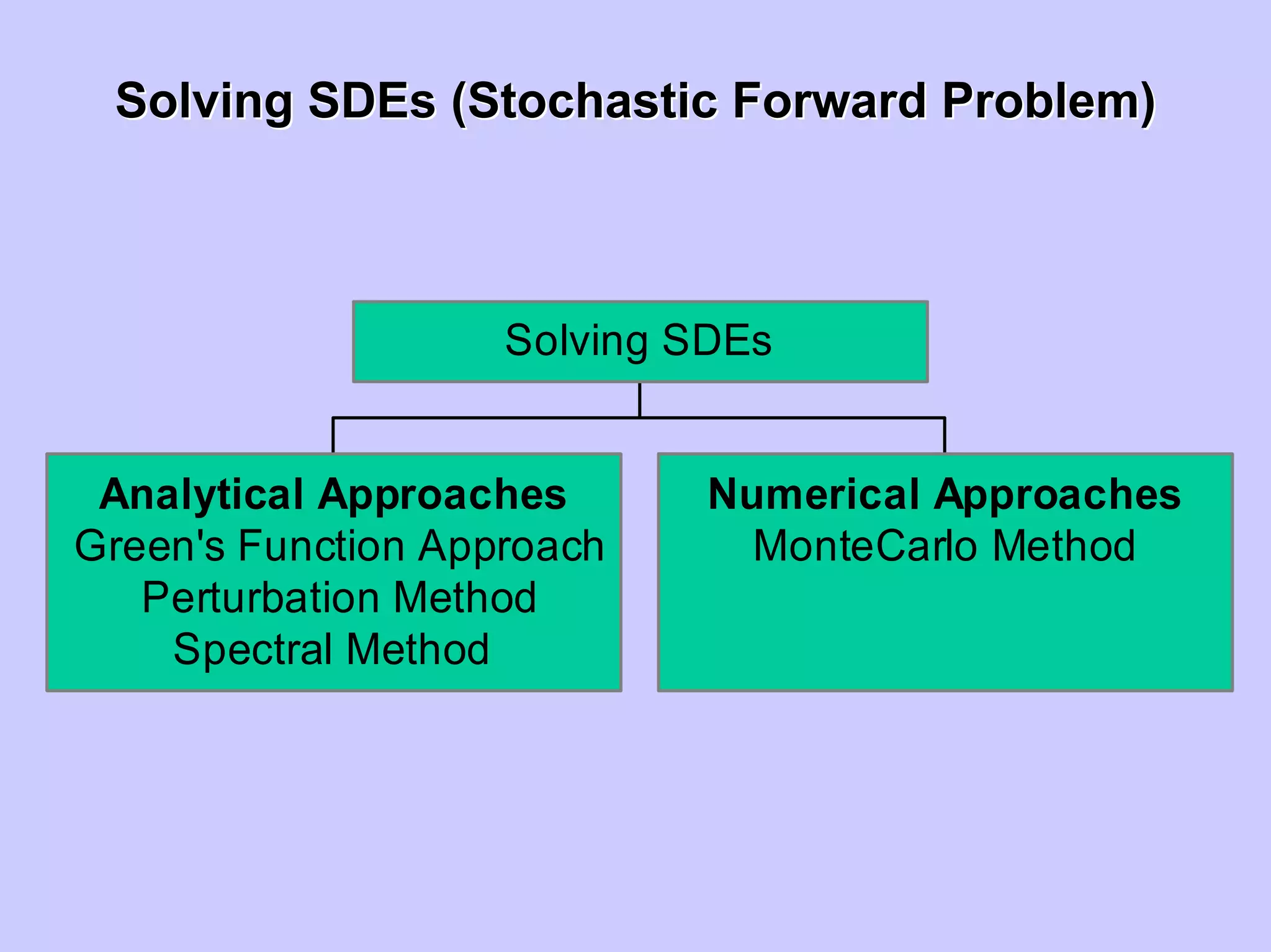
Stochastic differential equations (SDEs) describe systems with random components. Common methods to solve SDEs include spectral and perturbation methods. The spectral method represents variables and parameters as mean values plus fluctuations. Taking the expected value of the SDE yields equations for the mean and fluctuations that can be solved. The perturbation method expresses variables and parameters as power series expansions. Introducing these into the SDE allows analytical or numerical solution. SDEs are used to model systems with uncertain parameters like groundwater flow with random hydraulic conductivity.

1. Lecture (5)Lecture (5)
Stochastic Differential Equations
and
Methods of Solution:
Theory and Exercise

2. Stochastic Differential EquationsStochastic Differential Equations
TheoryTheory

3. Stochastic Differential Equations (Stochastic Differential Equations (SDEsSDEs))
Stochastic differential equation (SDE) = Differential equations for random
functions (stochastic processes)
= Classical differential equation (DE) +
Random functions, coefficients, parameters and boundary or initial values,
e.g.
( , ) ( , ) 0
where ( , ) ( , ) are random space functions.and
or stationary processes.
xx yy
xx yy
Φ Φ
x y + x y = ΩK K
x x y y
x y x yKK
⎛ ⎞∂ ∂ ∂ ∂⎛ ⎞
∈⎜ ⎟⎜ ⎟
∂ ∂ ∂ ∂⎝ ⎠ ⎝ ⎠
Stochastic Forward Problem

4. SolvingSolving SDEsSDEs (Stochastic Forward Problem)(Stochastic Forward Problem)
Analytical Approaches
Green's Function Approach
Perturbation Method
Spectral Method
Numerical Approaches
MonteCarlo Method
Solving SDEs

5. Spectral MethodSpectral Method
The dependent variable and parameter in a stochastic differential equation are
represented in terms of
its mean or expected value denoted with an angle brackets,
and some fluctuations around the mean denoted by a prime,
where, Y is written as the perturbed parameter, 〈Y〉 is the mean or expected
value of the parameter, E{Y}, Y´ is a perturbation around the mean value of the
parameter, so E{Y´}= 0.
Similarly, Φ is the perturbed variable, 〈Φ〉 is the mean or expected value of the
variable, E{Φ}, and Φ` is a perturbation around the mean value of the variable,
E{Φ`}= 0.
Y Y Y′= +
′Φ = Φ + Φ

6. Spectral Method (Cont.)Spectral Method (Cont.)
Assumptions:
1. The perturbations are relatively small compared to the mean value, so that
second order terms involving products of small perturbations can be
neglected.
2. The stochastic inputs parameters and the outputs variables are second
order stationary so that they can be expressed in terms of the
representation theorem.
Procedure:
1. Introducing the expressions into the differential equation.
2. Taking the expected value of the equation results in two new equations,
one for the first moment (mean) and the other for the perturbations.
3. The first is a deterministic differential equation, which can be solved
analytically to get the solution for the mean of the dependent variable as a
function of the mean of the parameter.
4. The second equation is transformed in the spectral domain by using
Fourier-Stieltjes representation theorem.

7. Spectral Method (Cont.)Spectral Method (Cont.)
∫∫
∞
∞−
∞
∞−
=′=′ )(.......,.........)( kk kxkx
dZeΦdZeY Φ
i
Y
i
5. The following integral transformation is used,
Where k is wave number vector, x is space dimension vector,
Z(k) is a random function with orthogonal increments, i.e.,
non-overlapping differences are uncorrelated
and dZ(k) is complex amplitudes of the Fourier modes of wave number k.
The spectral density function SYY(k) of Y’ is related to the generalized Fourier
amplitude, dZY by
k=kifdk,kS=kdZ.kdZE
kkif,=kdZ.kdZE
YY
*
YY
*
YY
21121
2121
)()}()({
0)}()({ ≠
The asterisk, *, denotes the complex conjugate.

8. Spectral Method (Cont.)Spectral Method (Cont.)
6. By using the above representation and substituting them into the stochastic
differential equation of perturbation, one can get the spectrum of the variable as
a function of the spectrum of the parameter.
7. The spectral density function is the Fourier transform of its auto-covariance
function, which can be expressed mathematically as follows:
-1
( ) ( )
2
i
dS e C
π
∞
ΦΦ ΦΦ
−∞
= ∫
ks
k s s
where s = lag vector of the auto-covariance function.
8. By using Wiener-Khinchin theorem, one can write,
2
( ) ( )
(0)
-i
= dC e S
=Cσ
∞
ΦΦ ΦΦ
−∞
Φ ΦΦ
∫
ks
s k k

9. Example of the Spectral Method (1)Example of the Spectral Method (1)
0 5 10 15 20 25
X
6
7
8
9
10
K(X)
>
( ) 0
1-D Groundwater Flow Equation
d dH
K x
dx dx
⎡ ⎤
=⎢ ⎥⎣ ⎦
Where, K(x) is second order stationary stochastic process and H is the head.

10. Example of the Spectral Method (2)Example of the Spectral Method (2)
( ) 0
d dH
K x
dx dx
⎡ ⎤
=⎢ ⎥⎣ ⎦
By Integration the equation leads to,
( )
d dH
K x dx q
dx dx
⎡ ⎤
= −⎢ ⎥⎣ ⎦
∫
dH q
qW
dx K
= − = −
Where, W is called the hydraulic resistivity =1/K ,
W is regarded as spatial stochastic process and
consequently the equation is stochastic ODE, and
The solution H will be a stochastic process.

11. Example of the Spectral Method (3)Example of the Spectral Method (3)
1. Introducing the expressions into the differential equation
, { } , { } 0
1
, { } , { } 0
H H h E H H E h
W W w E W W E w
K
= + = =
= = + = =
Substitution in the equation we obtain,
.
dH
qW
dx
= −
( )
( )
d H h
q W w
dx
+
= − +

12. Example of the Spectral Method (4)Example of the Spectral Method (4)
{ }
( )
( )
2. Taking the expected value of the equation results in two
new equations, one for the first moment (mean) and
the other for the perturbations.
( )
. 0
d H h
q W w
dx
d H h
E q E W w
dx
d H dh
E E
dx d
+
= − +
⎧ ⎫+
+ + =⎨ ⎬
⎩ ⎭
⎧ ⎫
+⎨ ⎬
⎩ ⎭
{ } { }( )
{ } { }( )
{ }
0
{ } { }
0
{ } { }
q E W E w
x
dE H dE h
q E W E w
dx dx
dE H dE h
qE W
dx dx
⎧ ⎫
+ + =⎨ ⎬
⎩ ⎭
+ + + =
+ + { }q E w+
{ }
0
by definition 0, { } 0E w E h
=
= =

13. Example of the Spectral Method (5)Example of the Spectral Method (5)
3. The first is a deterministic differential equation, which can be solved
analytically to get the solution for the mean of the dependent variable
as a function of the mean of the parameter.
{ }dE H
q
dx
+ { } 0
( )
Substitution in the first equation: ( ),
E W
d H
qW
dx
d H h
q W w
dx
d H
dx
=
= −
+
= − +
dh
qW
dx
+ = − qw
dh
qw
dx
−
= −

14. Example of the Spectral Method (6)Example of the Spectral Method (6)
4. The second equation is transformed in the spectral domain
by using Fourier-Stieltjes representation theorem.
~ , ~
( ) ( ); ( ) ( )
(
ikx ikx
w h
ikx
h
dh
qw
dx
w stationary h stationary
w x e dZ k h x e dZ k
d
e dZ k
dx
∞ ∞
−∞ −∞
∞
−∞
= −
= =∫ ∫
∫ ) ( )
( ) ( )
( ) ( )
( ) ( )
( )
( )
ikx
w
ikx ikx
h w
ikx ikx
h w
h w
w
h
q e dZ k
d
e dZ k q e dZ k
dx
ike dZ k q e dZ k
ikdZ k qdZ k
dZ k
dZ k q
ik
∞
−∞
∞ ∞
−∞ −∞
∞ ∞
−∞ −∞
⎛ ⎞
= −⎜ ⎟
⎝ ⎠
= −
= −
= −
= −
∫
∫ ∫
∫ ∫

15. Example of the Spectral Method (7)Example of the Spectral Method (7)
*
2
2
2
2
5. One can get the spectrum of the variable as a function of
the spectrum of the parameter as,
( ) ( ). ( )
( ) ( ) ( )
( ) , 1
( )
hh h h
w w ww
hh
hh
autoPSD S k dZ k dZ k
dZ k dZ k q S k
S k q q i
ik ik k
q
S k
k
= =
⎛ ⎞⎛ ⎞
= − = = −⎜ ⎟⎜ ⎟
⎝ ⎠⎝ ⎠
⎛ ⎞
= ⎜
⎝ ⎠
2 2 2
2 2 2
2
( )
assume the following spectral density of ( ),
2
( )
(1 )
( ) 1
ww
w
ww
s
l
ww w
S k
w
l k
S k hole effect
l k
s
C s e
l
σ
π
σ
−
⎟
= −
+
⎛ ⎞
= −⎜ ⎟
⎝ ⎠

16. Example of the Spectral Method (8)Example of the Spectral Method (8)
2
2
6. The spectral density function is the Fourier transform of
its auto-covariance function, which can be expressed mathematically
as follows:
( ) ( )
( )
( )
iks
hh hh
iks
ww
hh
C s e S k dk
q
S k e dk
k
C s q
∞
−∞
∞
−∞
=
=
=
∫
∫
2 2 2
2
2 2 2 2
2 2 2
2 2 2 2
21
(1 )
( ) 1
(0)
iksw
s
l
hh w
h hh w
l k
e dk
k l k
s
C s q l e
l
C q l
σ
π
σ
σ σ
∞
−∞
−
+
⎛ ⎞
= +⎜ ⎟
⎝ ⎠
= =
∫

17. Analytical Solution in 2D Unbounded FlowAnalytical Solution in 2D Unbounded Flow
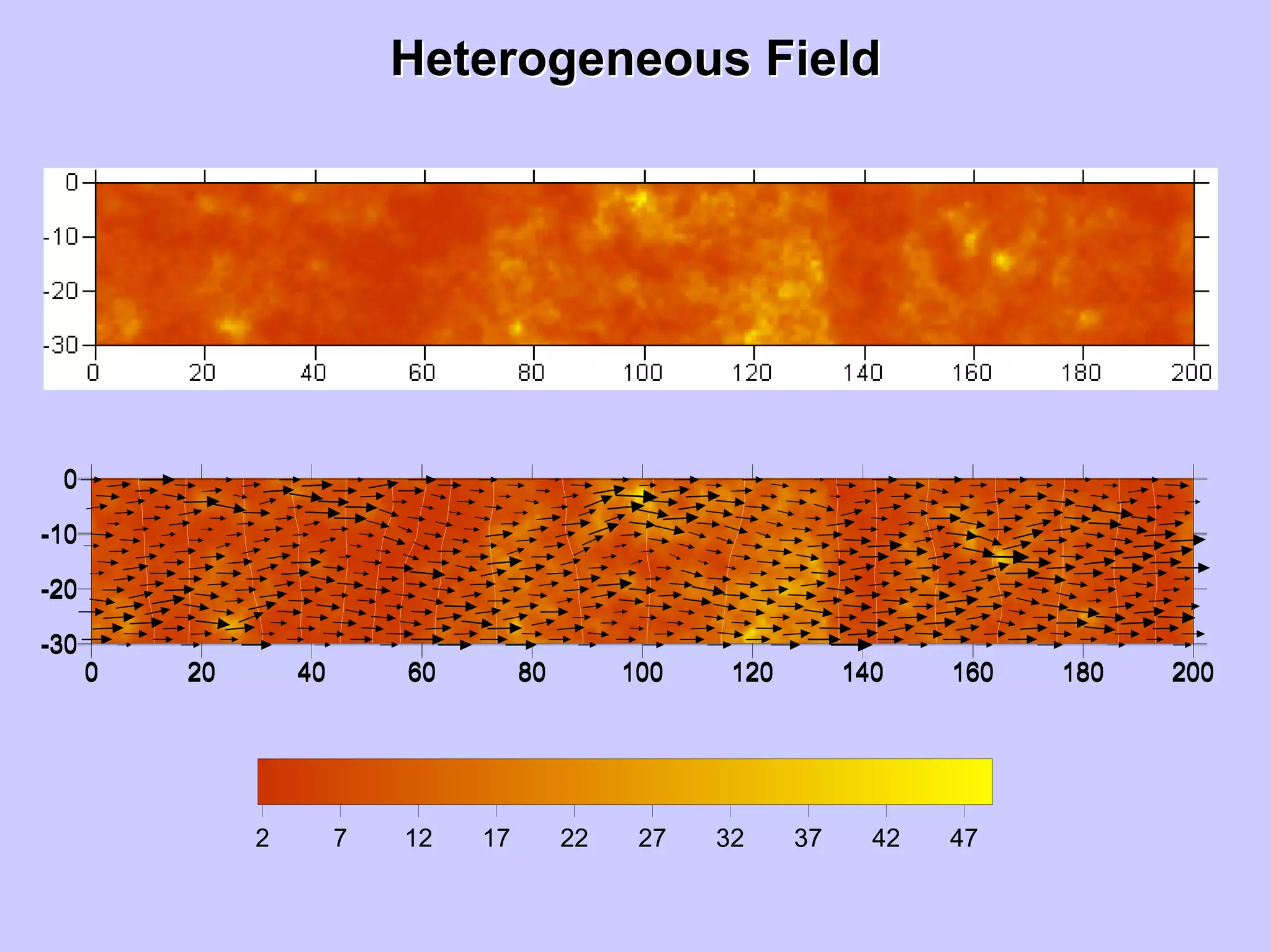
FieldField
( )
2 2
2
3/ 22 2
2 2 2 2
2 2 2
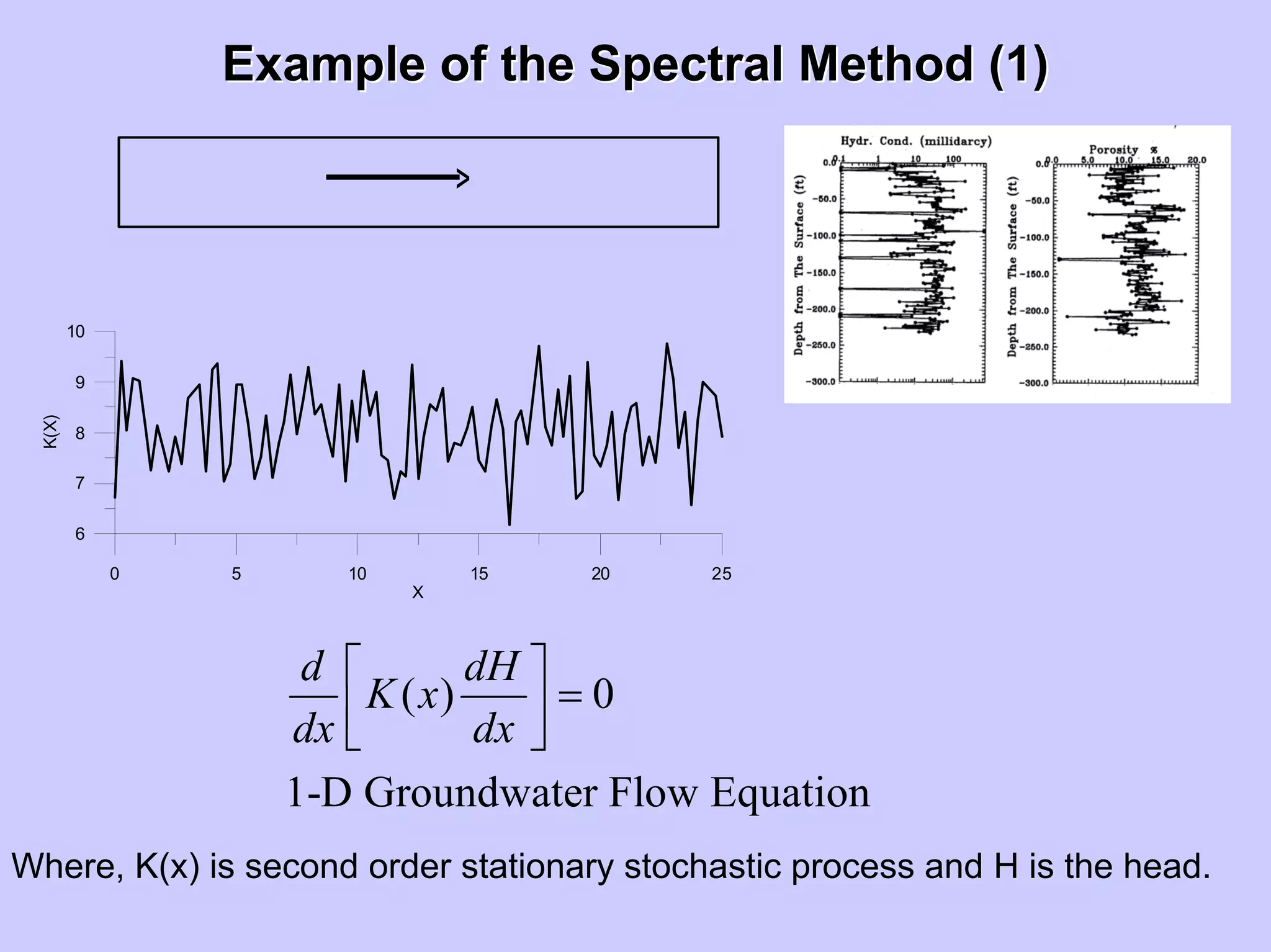
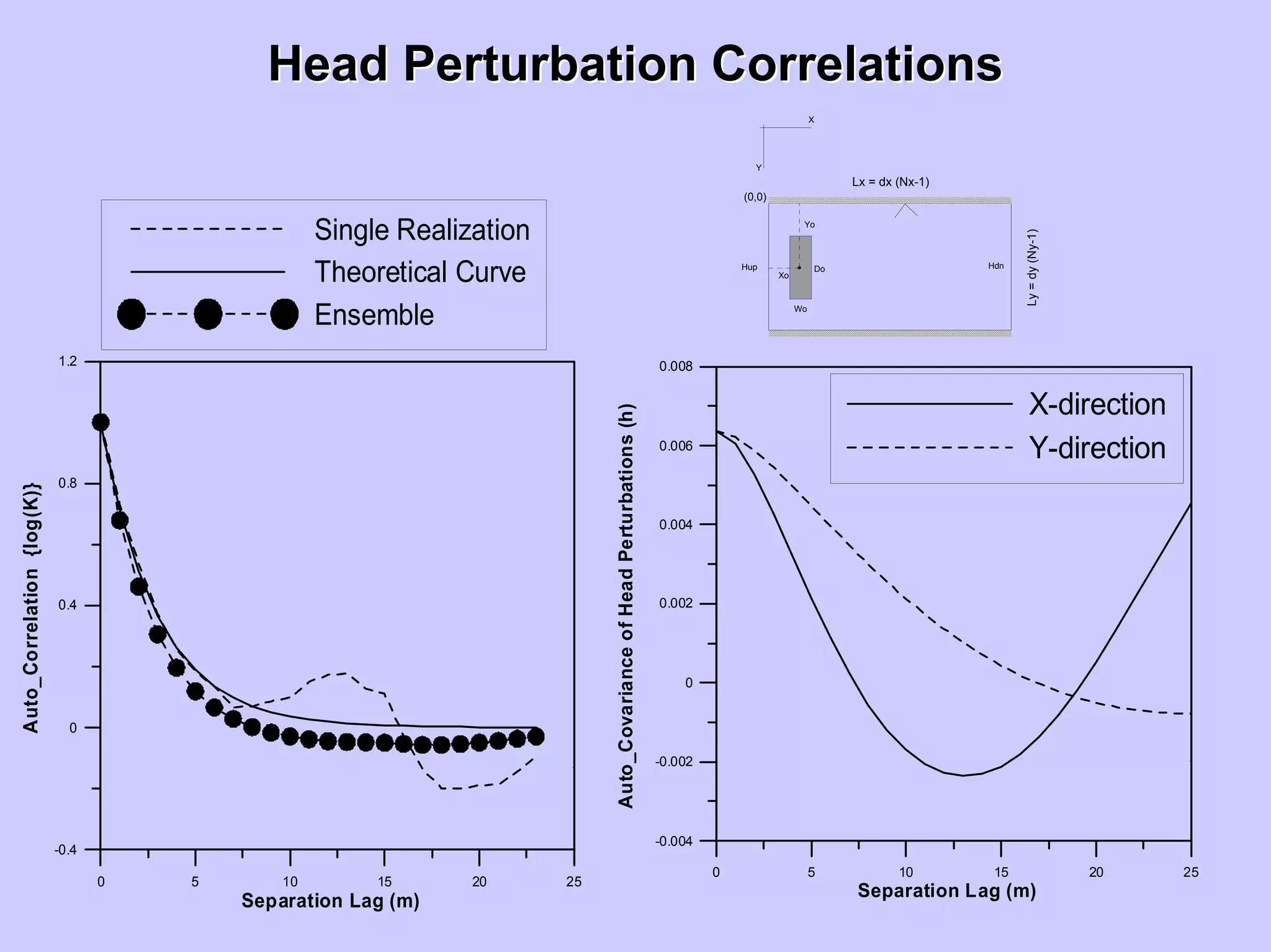
In 2D flow domain with exponential isotropic
covariance of Y=ln (K) given by,
( ) , ( )
2 1
The perturbation solution is given by Dagan [1989],
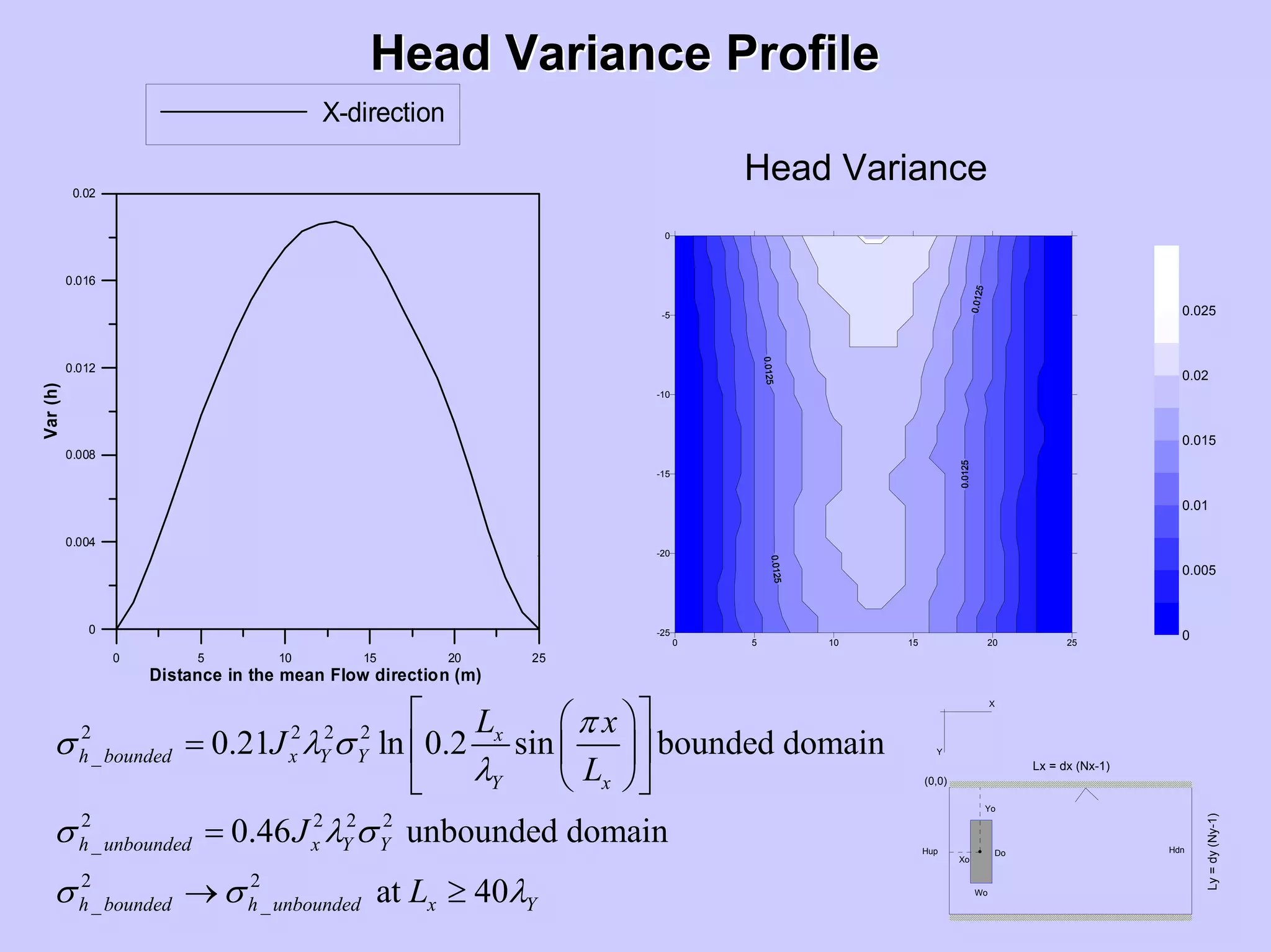
0.46
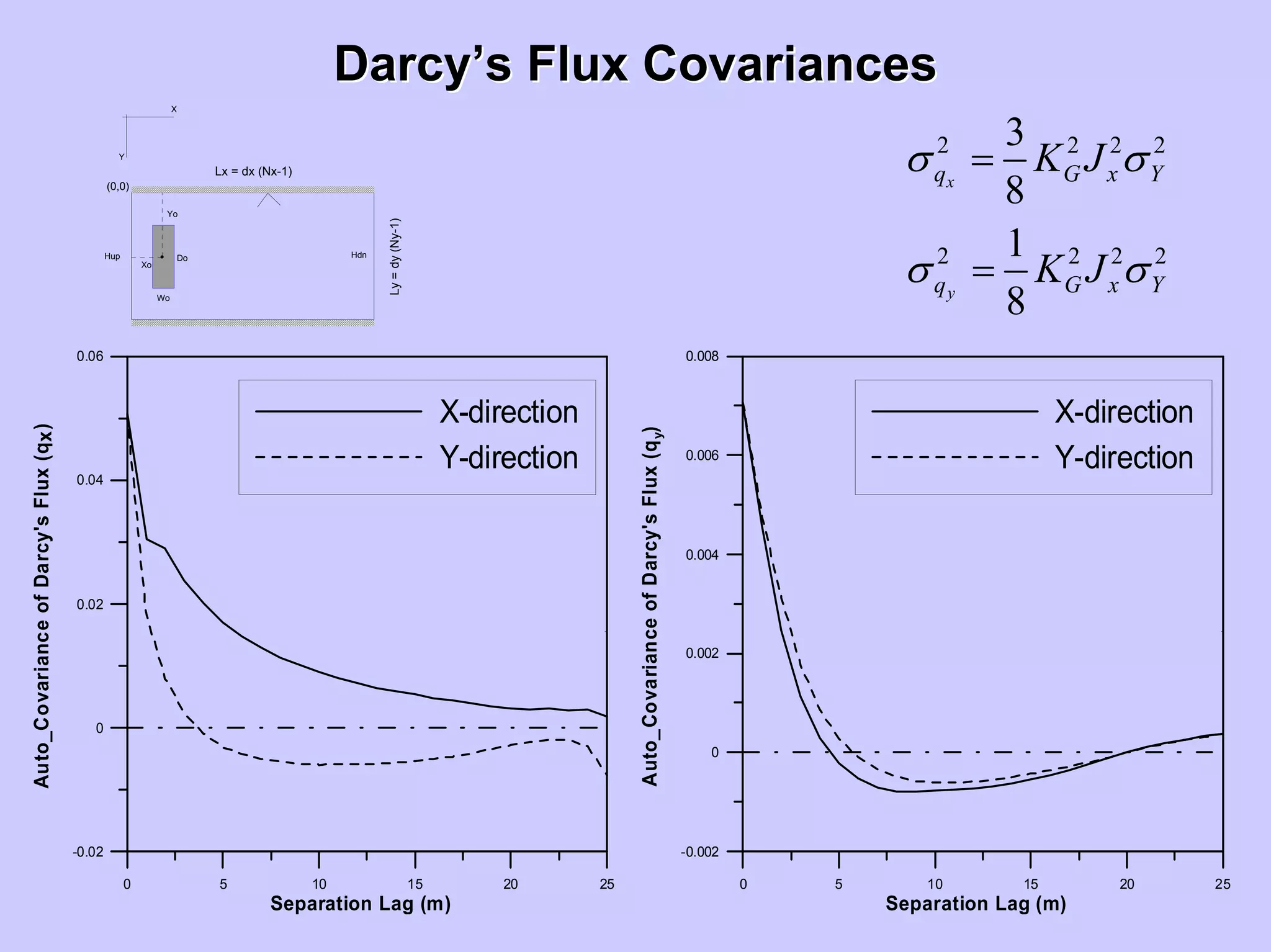
3
8
Y
x
Y Y
YY Y YY
Y
h x Y Y
q G x
C e S
J
K J
λ σ λ
σ
π λ
σ λ σ
σ σ
−
= =
+
=
=
s
s k
k
2
2 2 2 2
1
2
1
8
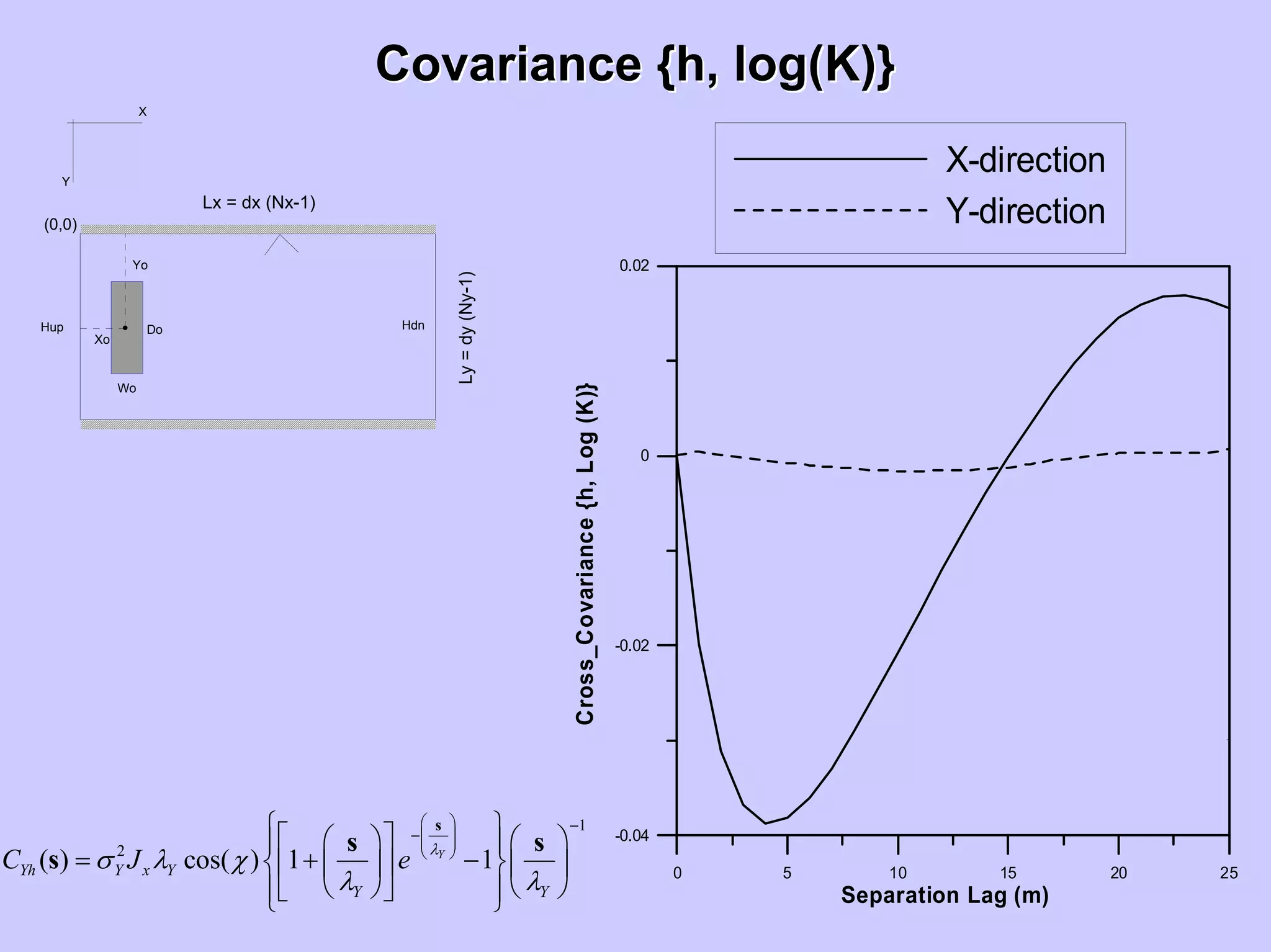
( ) cos( ) 1 1
y
Y
Y
q G x Y
Yh Y x Y
Y Y
K J
C J e
λ
σ σ
σ λ χ
λ λ
⎛ ⎞ −
−⎜ ⎟⎜ ⎟
⎝ ⎠
=
⎧ ⎫⎡ ⎤⎛ ⎞ ⎛ ⎞⎪ ⎪
= + −⎨ ⎬⎢ ⎥⎜ ⎟ ⎜ ⎟
⎝ ⎠ ⎝ ⎠⎣ ⎦⎪ ⎪⎩ ⎭
s
s s
s

18. Example of Stochastic TransportExample of Stochastic Transport EqEq.(1).(1)
( ) 0
( )
( )
( )
.
{ }
{ } { }.
. .
i
i i
i
i i
C C
V y
t x
K y
V y J
V y V
X V t
E K
E X E V t J
K
X V t J t
∂ ∂
+ =
∂ ∂
=
=
=
= =
= =
ε
ε
ε
Where, V(y) is second order stationary stochastic process and C is
concentration, K(y) is the permeability, J is pressure gradient, and
is porosity
4 6 8 10 12
Permeability
0
10
20
30
40
50
Depth
ε

19. Example of Stochastic TransportExample of Stochastic Transport EqEq.(2).(2)
2
2 2 2 2 2
2
22 2
22
2 2 2 2 2
2 2
2
22 2 2
2
2
2 2 2
2
2 2
2
2
. .
. .
.
.
1
.
2
X
X
X
X K
X
xx K
K
X V t J t
X X
K K
J t J t
J
K K t
J
t
d J
D t
dt
ε
σ
σ
ε ε
σ
ε
σ σ
ε
σ
σ
ε
= =
= −
= −
⎡ ⎤= −
⎣ ⎦
=
= =

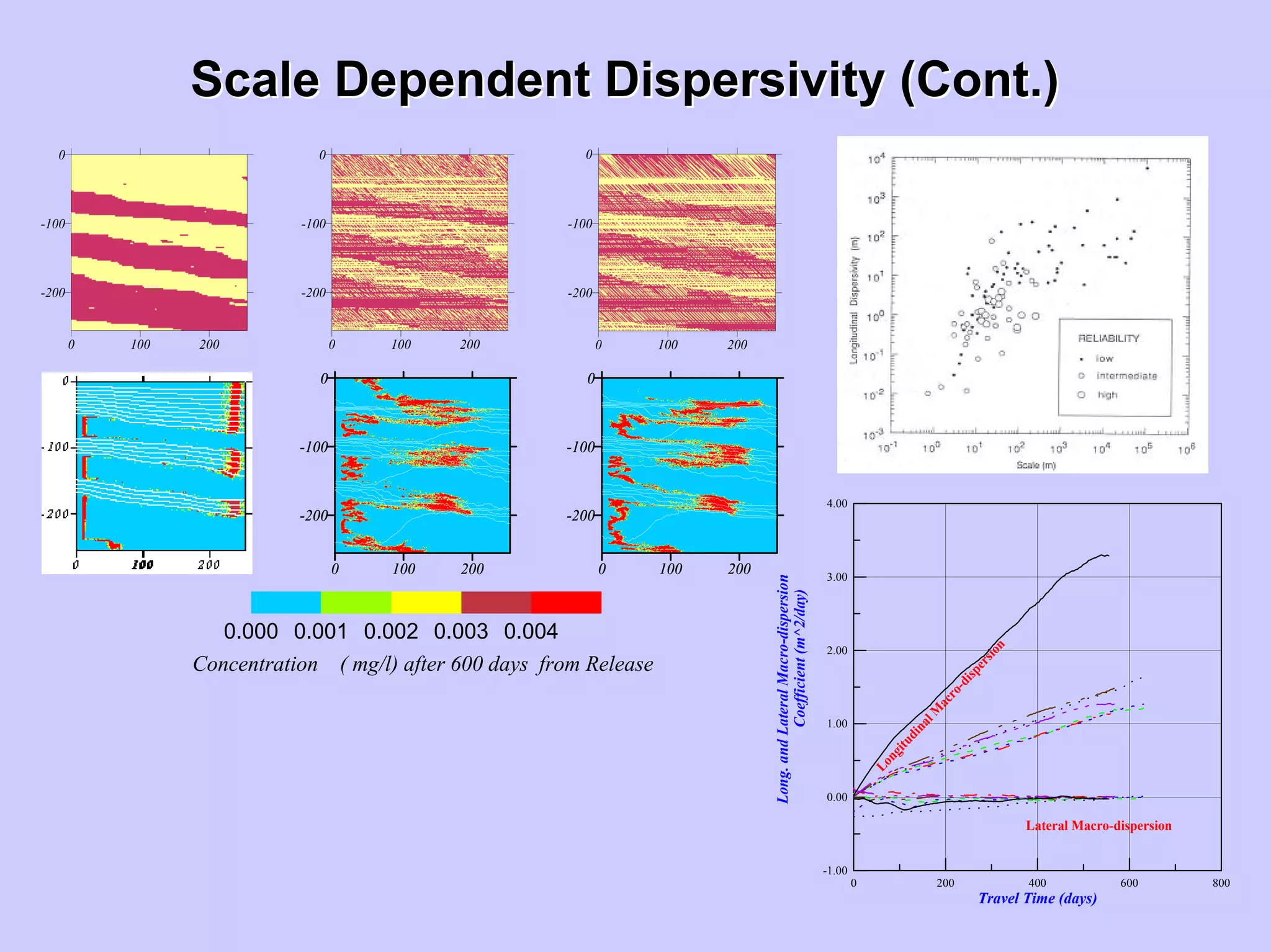
20. ScaleScale--DependentDependent DispersivityDispersivity
Field Longitudinal Dispersivity Data Classified According to Reliability
[after Gelhar, et al., 1992],

21. Scale DependentScale Dependent DispersivityDispersivity (Cont.)(Cont.)
Concentration ( mg/l) after 600 days from Release
0 100 200
-200
-100
0
0 100 200
-200
-100
0
0 100 200
-200
-100
0
0 100 200
-200
-100
0
0 100 200
-200
-100
0
0 100 200
-200
-100
0
0 100 200
-200
-100
0
0.000 0.001 0.002 0.003 0.004
0 200 400 600 800
Travel Time (days)
-1.00
0.00
1.00
2.00
3.00
4.00
Long.andLateralMacro-dispersion
Coefficient(m^2/day)
Lateral Macro-dispersion
LongitudinalM
acro-dispersion

22. Perturbation MethodPerturbation Method
The parameter,Y, (e.g. conductivity) and the variable, Φ, (e.g. head) can be
expressed in a power series expansion as,
2
1 2
2
1 2
......
......
o
o
Y Y Y Yβ β
β β
= + +
Φ = + +Φ Φ Φ
where, β is a small parameter (smaller than unity).
These expressions are introduced in the differential equations of the system to
get a set of equations in terms of zero- and higher-order expressions of the
factor β.
The equation that is in terms of zero β corresponds to the mean head.
The equation that is in terms of first-order of β corresponds to the head
perturbation.
In practice, only two or three terms of the series are usually evaluated.

23. MonteMonte--Carlo MethodCarlo Method
1. Assumption of the pdf of the model parameters or joint pdf. The pdfs are
based on some field tests and/or laboratory tests.
2. Generation of random fields of the hydrogeological parameters to represent
the heterogeneity of the formation.
3. By using a random number generator, one generates a realization for each
one of these parameters. The parameter generation can be correlated or
uncorrelated depending on the type of the problem.
4. With this parameter realization a classical numerical flow or/and transport
model is run and a set of results is obtained.
5. Another random selection of the parameters is made and the model is run
again, and so on.
6. It's necessary to have a very large number of runs, and the output model
results corresponding to each input is obtained which can be represented
mathematically by the stochastic process Φ(x,ζi).
7. Statistical analysis of the ensemble of the output (i.e. Φ(x,ζi) for i = 1,2,...m,
can be made to get the mean, the variance, the covariance or the
probability density function for each node with a location x in the grid.

24. Example of MC_FLOWExample of MC_FLOW
10 20 KBAR SDK
6 NO. OF CLASSES
25 25 LX LY
3 3 1000 lx ly Mc
1 1 dx dy
0.001 10000 eps maxit
5 4 upstream downstream
1 12 seed knorm
1 porosity
0 5 10 15 20 25
-25
-20
-15
-10
-5
0
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
Single Realization ln (K)
0 5 10 15 20 25
-25
-20
-15
-10
-5
0
0 5 10 15 20 25
-25
-20
-15
-10
-5
0

25. Random Field CorrelationRandom Field Correlation
0 5 10 15 20 25
Separation Lag (m)
-0.4
0
0.4
0.8
1.2
Auto_Correlation{log(K)}
Single Realization
Theoretical Curve
Ensemble

26. Flow and Transport DomainFlow and Transport Domain
,
Lx = dx (Nx-1)
Ly=dy(Ny-1)
X
Y
(0,0)
Yo
Xo
Do
Wo
Hup Hdn

27. Single Realization Head FieldSingle Realization Head Field
0 5 10 15 20 25
-25
-20
-15
-10
-5
0
0 5 10 15 20 25
-25
-20
-15
-10
-5
0
0 5 10 15 20 25
-25
-20
-15
-10
-5
0
3.95 4.05 4.15 4.25 4.35 4.45 4.55 4.65 4.75 4.85 4.95
0 5 10 15 20 25
-25
-20
-15
-10
-5
0
-0.14
-0.1
-0.06
-0.02
0.02
0.06
0.1
0.14
0.18
0.22
Single Realization ln (K)
Single Realization (Head) Theoretical Ensemble Head Head Perturbation
,
Lx = dx (Nx-1)
Ly=dy(Ny-1)
X
Y
(0,0)
Yo
Xo
Do
Wo
Hup Hdn

28. Single Realization of DarcySingle Realization of Darcy’’s Fluxess Fluxes
0 5 10 15 20 25
-25
-20
-15
-10
-5
0
0 5 10 15 20 25
-25
-20
-15
-10
-5
0
0 5 10 15 20 25
-25
-20
-15
-10
-5
0
0 5 10 15 20 25
-25
-20
-15
-10
-5
0

29. Single Realization Head Gradient ProfileSingle Realization Head Gradient Profile
0 5 10 15 20 25Distance in the mean Flow direction (m)
4
4.2
4.4
4.6
4.8
5
Head(m)
Mean Head
Single Realization
0 5 10 15 20 25Distance in the mean Flow direction (m)
0
2
4
Head(m)
Mean Head
Single Realization
log(K)- Realization

30. Ensemble Head FieldEnsemble Head Field
0 5 10 15 20 25
-25
-20
-15
-10
-5
0
0 5 10 15 20 25
-25
-20
-15
-10
-5
0
3.95 4.05 4.15 4.25 4.35 4.45 4.55 4.65 4.75 4.85 4.95
0
0.005
0.01
0.015
0.02
0.025
0 5 10 15 20 25
-25
-20
-15
-10
-5
0
Head VarianceEnsemble Head
( , ) ( )up up down
x
x
H x y H H H
L
= − −

31. HeadHead VariogramsVariograms
0 5 10 15 20 25
Separation Lag (m)
0
0.1
0.2
0.3
0.4
0.5
VariogramoftheHead(H)
X-direction
Y-direction
0 5 10 15 20 25
Separation Lag (m)
0
0.002
0.004
0.006
0.008
0.01
VariogramoftheHead(H)
Y-direction
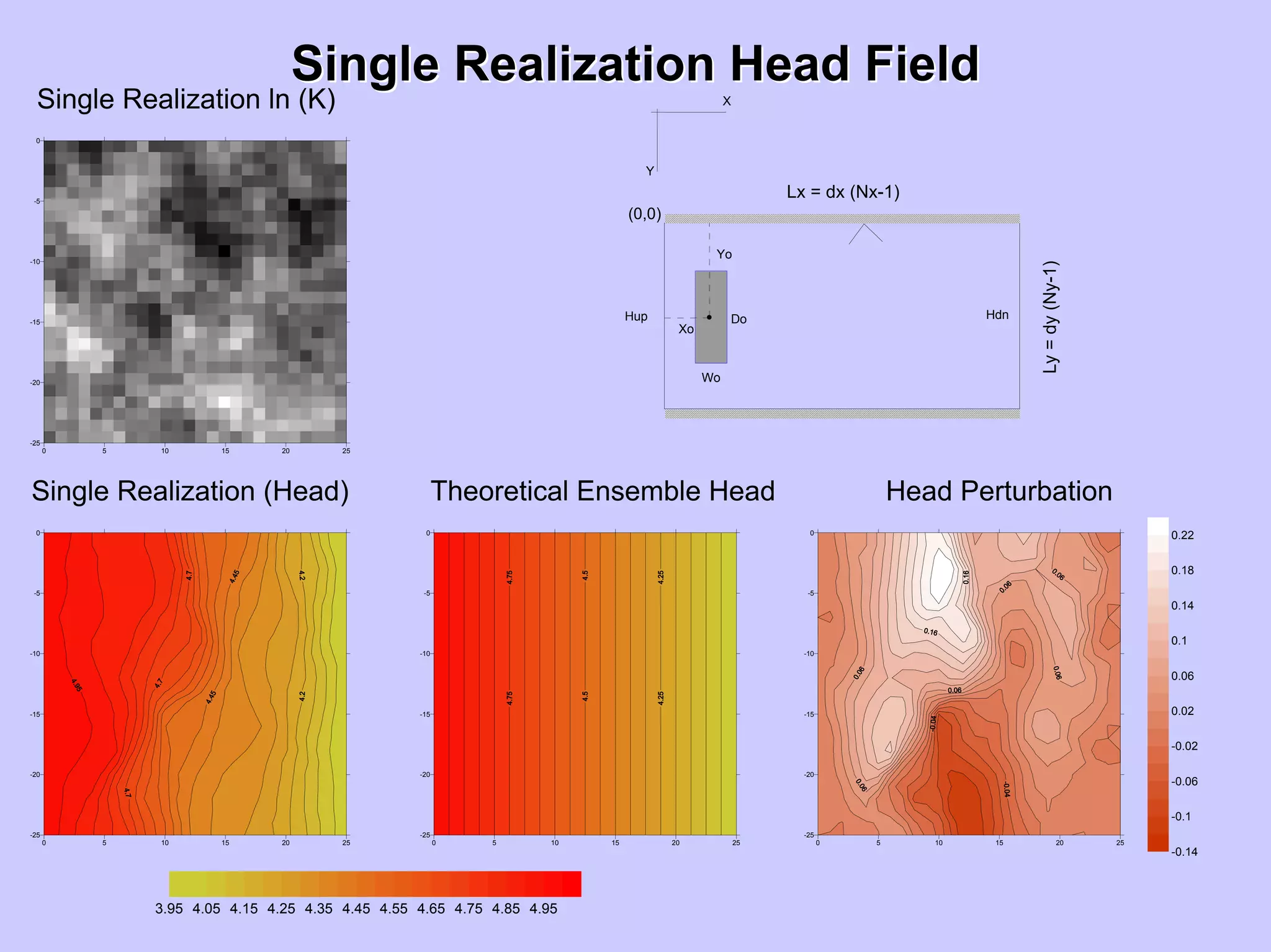
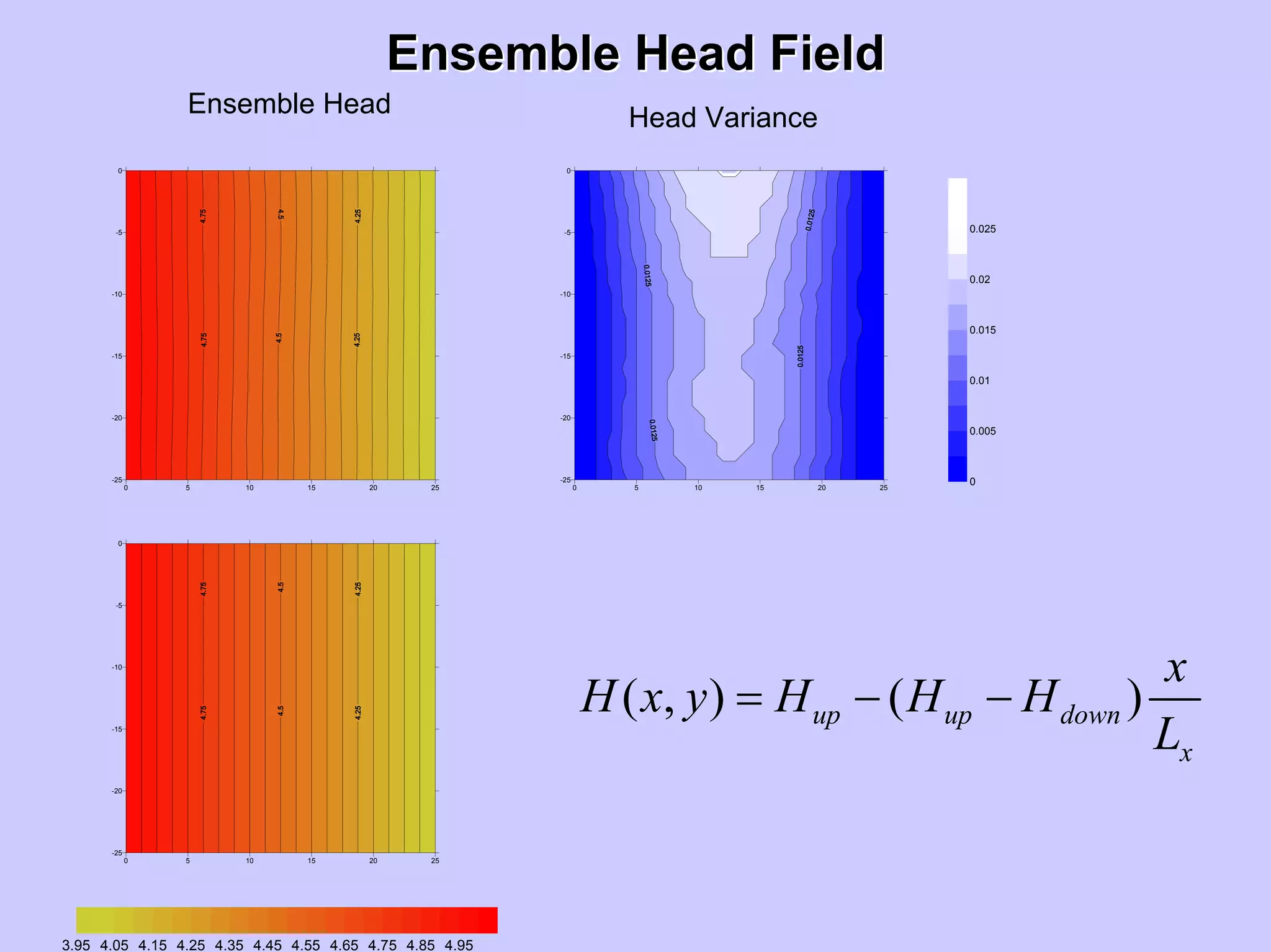
( , ) ( )up up down
x
x
H x y H H H
L
= − −
[ ]
( )
2
1
1
( ) ( )- ( )
2 ( )
n
i
Z Z
n
γ
=
= ∑
s
s x +s x
s ,
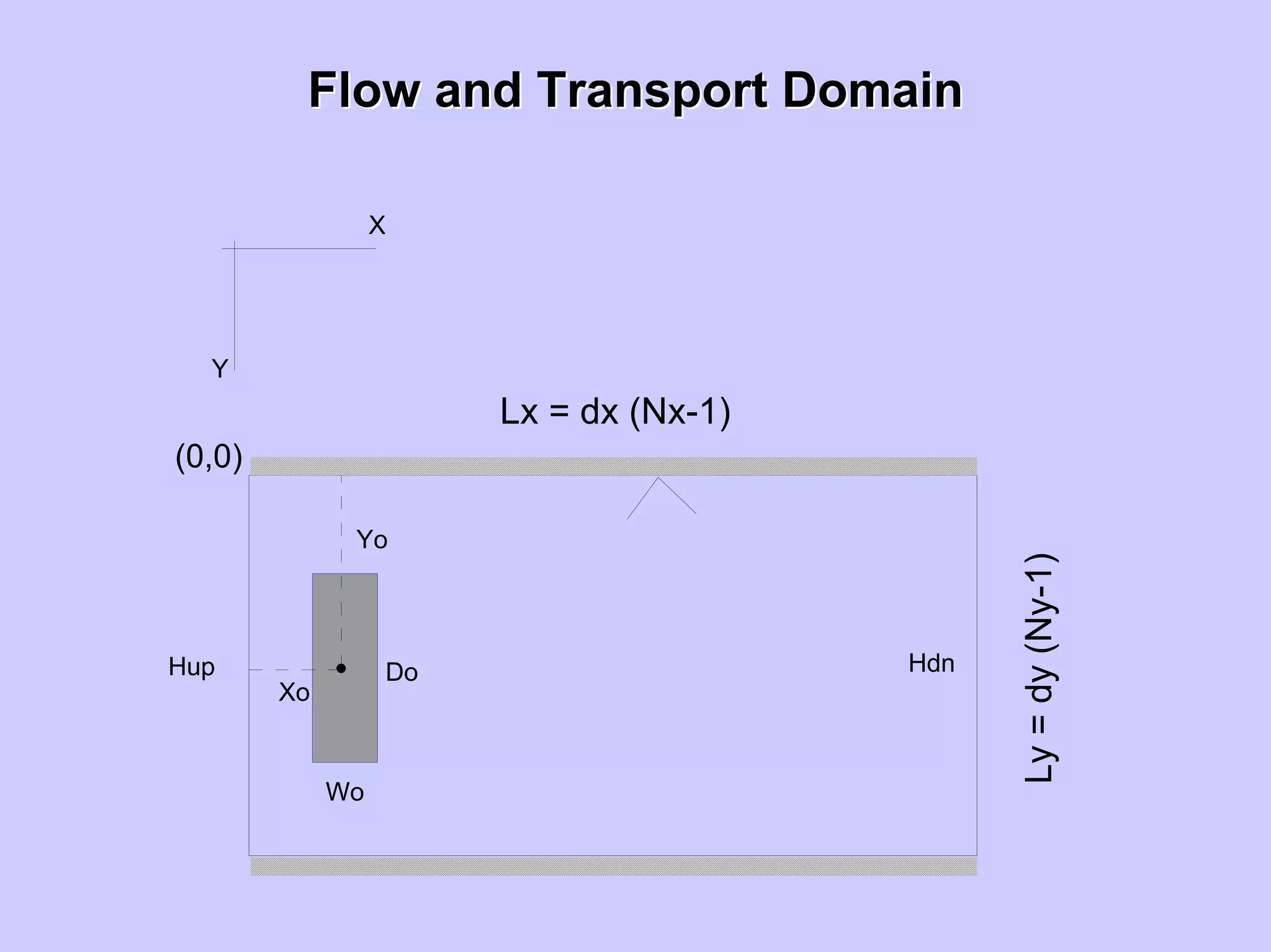
Lx = dx (Nx-1)
Ly=dy(Ny-1)
X
Y
(0,0)
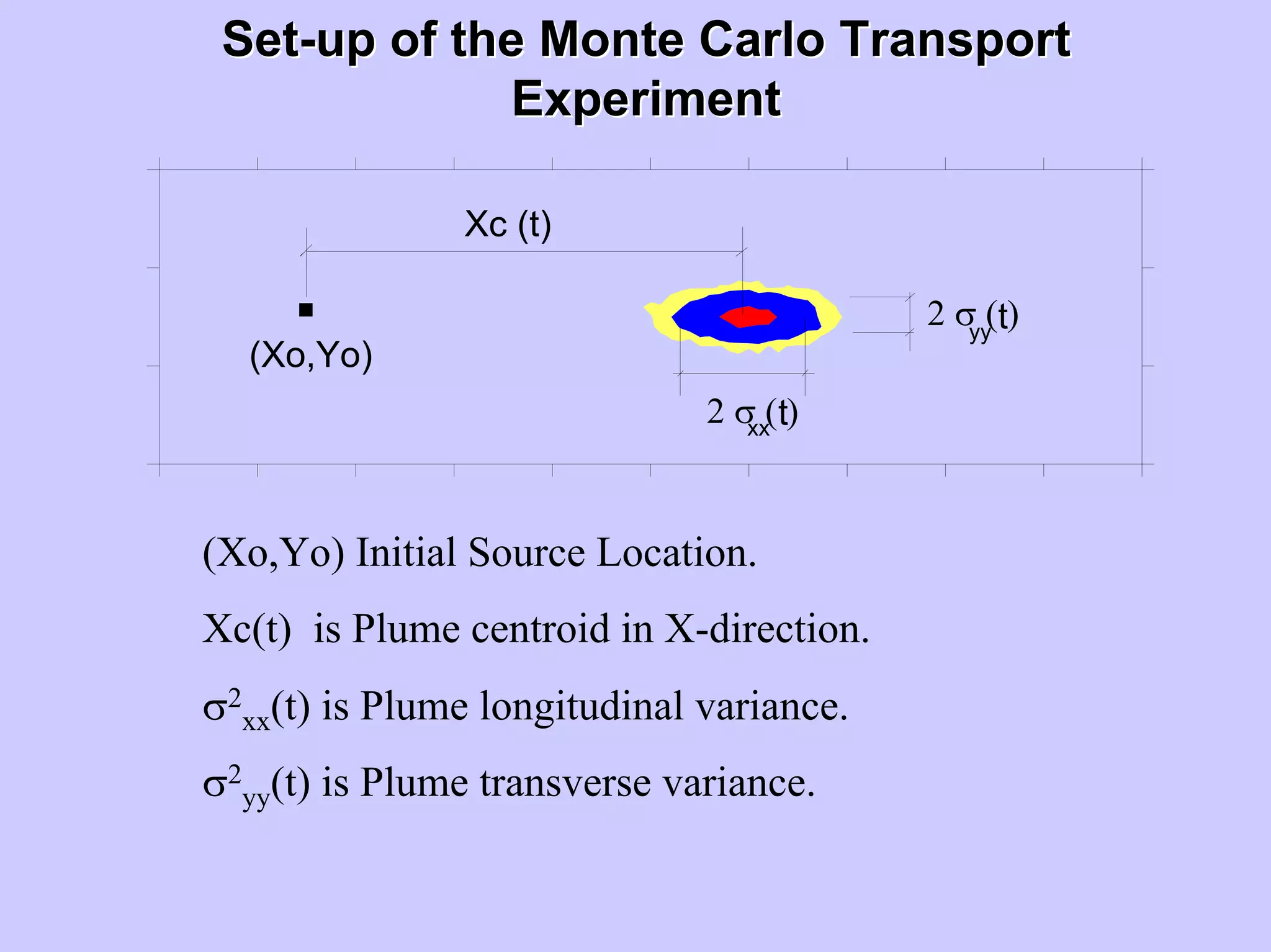
Yo
Xo
Do
Wo
Hup Hdn

32. Head Perturbation CorrelationsHead Perturbation Correlations
0 5 10 15 20 25
Separation Lag (m)
-0.004
-0.002
0
0.002
0.004
0.006
0.008
Auto_CovarianceofHeadPerturbations(h)
X-direction
Y-direction
0 5 10 15 20 25
Separation Lag (m)
-0.4
0
0.4
0.8
1.2
Auto_Correlation{log(K)}
Single Realization
Theoretical Curve
Ensemble
,
Lx = dx (Nx-1)
Ly=dy(Ny-1)
X
Y
(0,0)
Yo
Xo
Do
Wo
Hup Hdn

33. Head Variance ProfileHead Variance Profile
0 5 10 15 20 25
Distance in the mean Flow direction (m)
0
0.004
0.008
0.012
0.016
0.02
Var(h)
X-direction
0 5 10 15 20 25
-25
-20
-15
-10
-5
0
0
0.005
0.01
0.015
0.02
0.025
Head Variance
2 2 2 2
_
2 2 2 2
_
2 2
_ _
0.21 ln 0.2 sin bounded domain
0.46 unbounded domain
at 40
x
h bounded x Y Y
Y x
h unbounded x Y Y
h bounded h unbounded x Y
L x
J
L
J
L
⎡ ⎤⎛ ⎞
= ⎢ ⎥⎜ ⎟
⎝ ⎠⎣ ⎦
=
→ ≥
π
σ λ σ
λ
σ λ σ
σ σ λ
,
Lx = dx (Nx-1)
Ly=dy(Ny-1)
X
Y
(0,0)
Yo
Xo
Do
Wo
Hup Hdn

34. Covariance {h, log(K)}Covariance {h, log(K)}
0 5 10 15 20 25
Separation Lag (m)
-0.04
-0.02
0
0.02
Cross_Covariance{h,Log(K)}
X-direction
Y-direction
,
Lx = dx (Nx-1)
Ly=dy(Ny-1)
X
Y
(0,0)
Yo
Xo
Do
Wo
Hup Hdn
1
2
( ) cos( ) 1 1Y
Yh Y x Y
Y Y
C J e
λ
σ λ χ
λ λ
⎛ ⎞ −
−⎜ ⎟⎜ ⎟
⎝ ⎠
⎧ ⎫⎡ ⎤⎛ ⎞ ⎛ ⎞⎪ ⎪
= + −⎨ ⎬⎢ ⎥⎜ ⎟ ⎜ ⎟
⎝ ⎠ ⎝ ⎠⎣ ⎦⎪ ⎪⎩ ⎭
s
s s
s

35. DarcyDarcy’’s Fluxs Flux CovariancesCovariances
,
Lx = dx (Nx-1)
Ly=dy(Ny-1)
X
Y
(0,0)
Yo
Xo
Do
Wo
Hup Hdn
2 2 2 2
2 2 2 2
3
8
1
8
x
y
q G x Y
q G x Y
K J
K J
σ σ
σ σ
=
=
0 5 10 15 20 25
Separation Lag (m)
-0.02
0
0.02
0.04
0.06
Auto_CovarianceofDarcy'sFlux(qx)
X-direction
Y-direction
0 5 10 15 20 25
Separation Lag (m)
-0.002
0
0.002
0.004
0.006
0.008
Auto_CovarianceofDarcy'sFlux(qy)
X-direction
Y-direction

36. Solute Transport EquationSolute Transport Equation
[ ] WCC
CQ
S
+CV
xx
C
D
xt
C
SinkSource
Decay
reactionChemicalAdvection
i
i
DiffusionDispersion
j
ij
i
/
)'(
ε
−
+λ−
ε∂
∂
−
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
∂
∂
∂
∂
=
∂
∂
−
−
where
C is the concentration field at time t,
S is solute concentration of species in the source or sink fluid,
i, j are counters,
C’ is the concentration of the dissolved solutes in a source or sink,
W is a general term for source or sink and
Vi is the component of the Eulerian interstitial velocity in xi direction
defined as follows,
Dij is the hydrodynamic dispersion tensor,
Q is the volumetric flow rate per unit volume of the source or sink,
j
ij
i
x
K
-=V
∂
Φ∂
ε
where
Kij is the hydraulic conductivity tensor, and ε is the porosity of the medium.

37. SetSet--up of the Monte Carlo Transportup of the Monte Carlo Transport
ExperimentExperiment
.
Xc (t)
2 σ ( )txx
2 σ ( )yy t
(Xo,Yo)
(Xo,Yo) Initial Source Location.
Xc(t) is Plume centroid in X-direction.
σ2
xx(t) is Plume longitudinal variance.
σ2
yy(t) is Plume transverse variance.

38. Heterogeneous FieldHeterogeneous Field
2 7 12 17 22 27 32 37 42 47
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0

39. Single Realization SimulationSingle Realization Simulation
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0.00 0.50 5.00 50.00
time = 100 days
time = 400 days
time = 1000 days
time = 1300 days
Concentration in mg/l
time = 600 days

40. MonteMonte--Carlo Method ResultsCarlo Method Results
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0.00 0.50 5.00 50.00
time = 100 days
time = 400 days
time = 1000 days
time = 1300 days
Concentration in mg/l
time = 600 days
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
2 7 12 17 22 27 32 37 42 47
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
0 20 40 60 80 100 120 140 160 180 200
-30
-20
-10
0
C <C> sC
sC
<C>
____

41. Comparison between Analytical andComparison between Analytical and
MonteCarloMonteCarlo MethodsMethods
Item Analytical MonteCarlo
Solution defined over a
continuum
defined over a grid.
Stationarity of the
variables
input and output
variables should be
stationary
no need for
stationarity
assumption.
Probability
distribution of input
variables
no need to define
PDF of the input
variable in some
applications.
the PDF of the input
variables must be
known.
Handling variability limited to small
variability.
not limited to small
variability.

42. Comparison between Analytical andComparison between Analytical and
MonteCarloMonteCarlo Methods (1)Methods (1)
Item Analytical MonteCarlo
Linearity versus non-
linearity
based on linearized
theories or weakly-
nonlinearity.
it can address both
cases.
Outcome of the
method
closed form solution
of moments.
(limited only for the
first two moments)
numerical values
used to calculate
moments of the
independent
variables. (One can
calculate the
complete PDF).

43. Comparison between Analytical andComparison between Analytical and
MonteCarloMonteCarlo Methods (2)Methods (2)
Item Analytical MonteCarlo
Spatial structure of
the variability
simple forms of auto-
covariance models
simple and
compound (nested)
forms of auto-
covariances.
Sources of errors number of simplifying
assumptions such as,
the form of mean and
covariance function,
the geometry of the
domain and the
boundary conditions.
sampling (finite
number of
realizations) and
discretization errors
are introduced
because of
approximation of the
governing equations.
Time and computer
effort
limited (to calculate
the values).
time consuming.

44. Comparison between Analytical and MonteComparison between Analytical and Monte--
Carlo Methods (3)Carlo Methods (3)
Item Analytical MonteCarlo
performing
conditioning to field
measurements
difficult easy
handling more than
one
stochastic variable
if it is possible, it is
too difficult.
it is easy to handle
more than one
variable.

45. Stochastic Differential EquationsStochastic Differential Equations
Computer ExerciseComputer Exercise

46. Input Data for MC_Flow
Mc_flow.dat
10 20 KBAR SDK
6 NO. OF CLASSES
25 25 LX LY
3 3 1000 lx ly Mc
1 1 dx dy
0.001 10000 eps maxit
5 4 upstream downstream
99991 12 seed knorm
1 porosity

47. Input Data for MC_Transport
Flow.datGeosim.dat Ranwalk.DAT
Rfield.dat Mc.dat