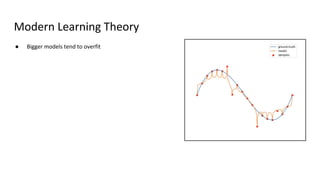
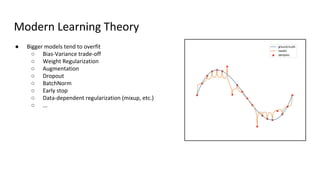
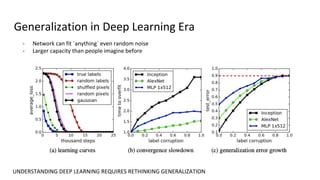
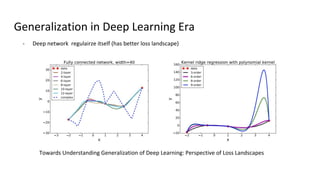
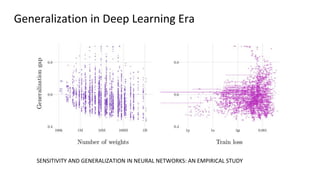
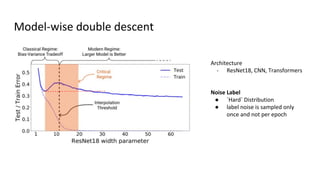
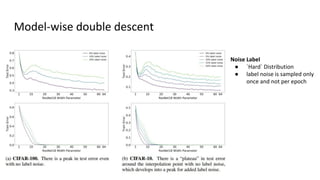
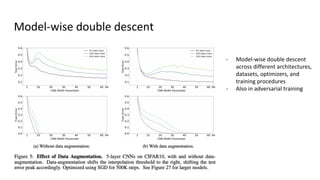
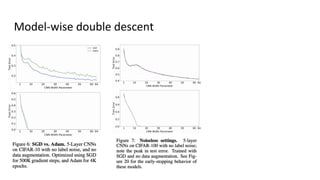
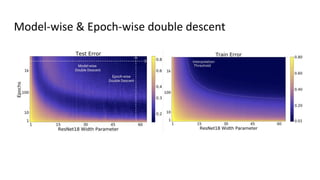
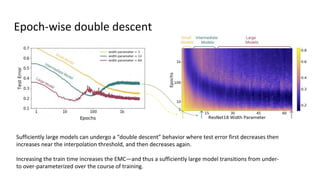
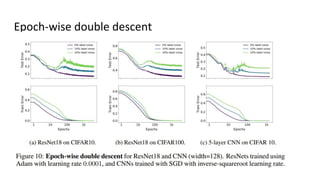
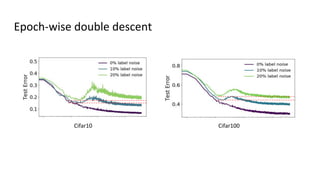
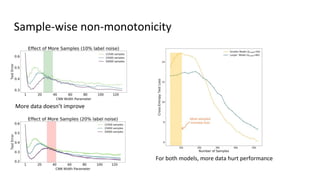
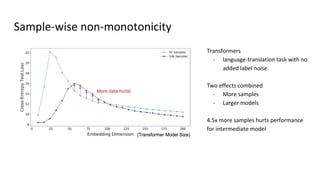
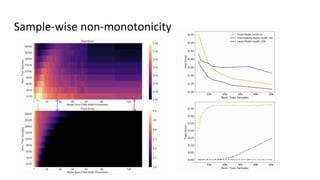
The document discusses deep double descent in modern learning theory, highlighting that larger models can overfit and may not always perform better. It describes instances where increasing training time or data can lead to worse performance, emphasizing the complexities of generalization in deep learning. Key concepts include model-wise and epoch-wise double descent, and the challenges of connecting data complexity with model complexity.

1. Deep Double Descent
kevin

2. Modern Learning Theory
● Bigger models tend to overfit

3. Modern Learning Theory
● Bigger models tend to overfit
○ Bias-Variance trade-off
○ Weight Regularization
○ Augmentation
○ Dropout
○ BatchNorm
○ Early stop
○ Data-dependent regularization (mixup, etc.)
○ ...

4. Modern Learning Theory
● Bigger models tend to overfit
● Bigger models are always better
Reconciling modern machine learning practice and the bias-variance trade-off

5. Modern Learning Theory
● Bigger models tend to overfit
● Bigger models are always better
● Bigger models not good in some regime
https://mltheory.org/deep.pdf

6. Modern Learning Theory
● Bigger models tend to overfit
● Bigger models are always better
● Bigger models not good in some regime
● Even more data hurt!
https://mltheory.org/deep.pdf

7. TL;DR
- Model-wise double descent
- There is a regime where bigger models are worse
- Sample-wise non-monotonicity
- There is a regime where more samples hurts
- Epoch-wise double descent
- There is a regime where training longer reverses overfitting

8. Generalization in Deep Learning Era
- Network can fit `anything` even random noise
- Larger capacity than people imagine before
UNDERSTANDING DEEP LEARNING REQUIRES RETHINKING GENERALIZATION

9. Generalization in Deep Learning Era
- Over-parameterized network performs
IN SEARCH OF THE REAL INDUCTIVE BIAS : ON THE ROLE OF IMPLICIT REGULARIZATION IN DEEP LEARNING

10. Generalization in Deep Learning Era
- Deep network regulairze itself (has better loss landscape)
Towards Understanding Generalization of Deep Learning: Perspective of Loss Landscapes

11. Generalization in Deep Learning Era
SENSITIVITY AND GENERALIZATION IN NEURAL NETWORKS: AN EMPIRICAL STUDY

12. Model-wise double descent
Architecture
- ResNet18, CNN, Transformers
Noise Label
● `Hard` Distribution
● label noise is sampled only
once and not per epoch

13. Model-wise double descent
Noise Label
● `Hard` Distribution
● label noise is sampled only
once and not per epoch

14. Model-wise double descent
- Model-wise double descent
across different architectures,
datasets, optimizers, and
training procedures
- Also in adversarial training

15. Model-wise double descent

16. Model-wise & Epoch-wise double descent

17. Epoch-wise double descent
Sufficiently large models can undergo a “double descent” behavior where test error first decreases then
increases near the interpolation threshold, and then decreases again.
Increasing the train time increases the EMC—and thus a sufficiently large model transitions from under-
to over-parameterized over the course of training.

18. Epoch-wise double descent
Conventional training is split into two phases:
1. In the first phase, the network learns a function with a small generalization gap
2. In the second phase, the network starts to over-fit the data leading to an increase in test error
Not the complete picture
- Some regimes, the test error decreases again and may achieve a lower value at the end of training
as compared to the first minimum
Reminds
- Information bottleneck
- Lottery ticket hypothesis

19. Epoch-wise double descent

20. Epoch-wise double descent
Cifar10 Cifar100

21. Sample-wise non-monotonicity
More data doesn’t improve
For both models, more data hurt performance

22. Sample-wise non-monotonicity
Transformers
- language-translation task with no
added label noise.
Two effects combined
- More samples
- Larger models
4.5x more samples hurts performance
for intermediate model

23. Sample-wise non-monotonicity

24. Conclusion
Take home message :
Model behaves unexpectedly in transition regime
- Training longer reverses overfitting
- Double the training epoch is a technique in some task
(eg. object detection)
- Bigger models are worse
- Fitting training set is an indicator
- Also called Effective Model Complexity (EMC)
- More data hurts
- sticky :(
- Generalization is still the Holy Grail in deep learning
- remains the open question (both exp. & theory)
- Connect data complexity with model complexity is still difficult
- NAS in some sence systematically solve this problem
Know your data & model
- noise level (problem difficulty)
- model capacity (fitting power)