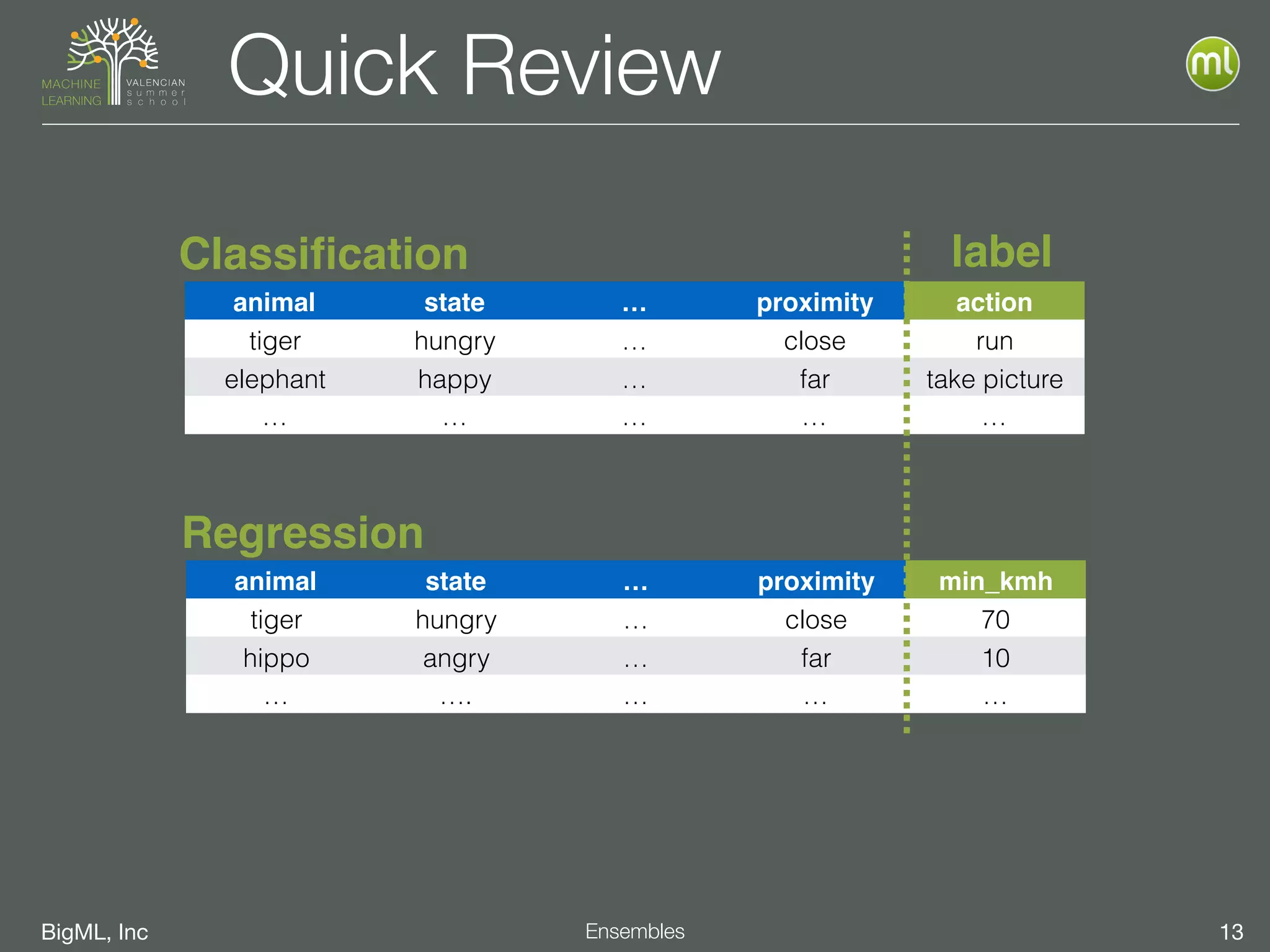
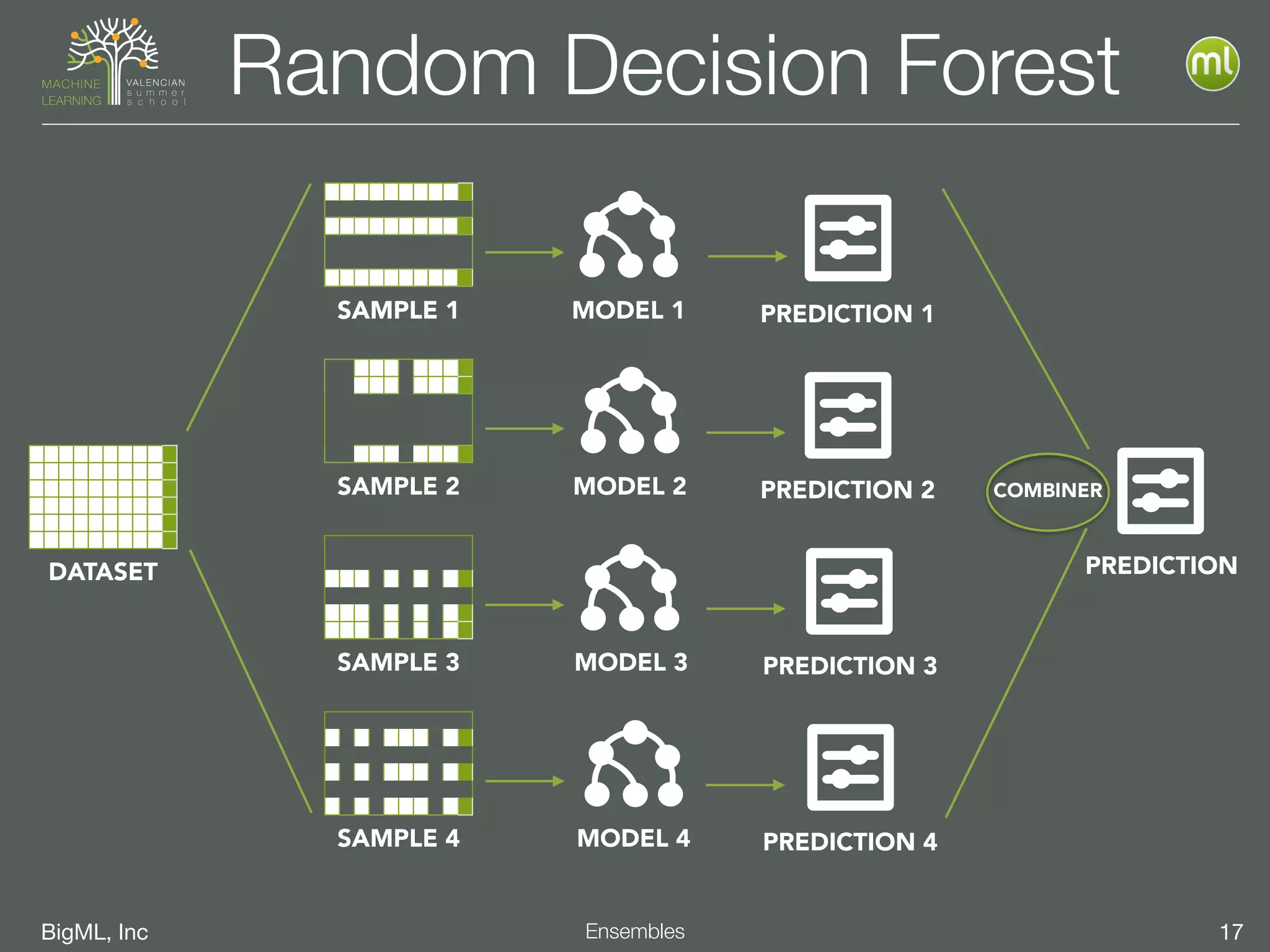
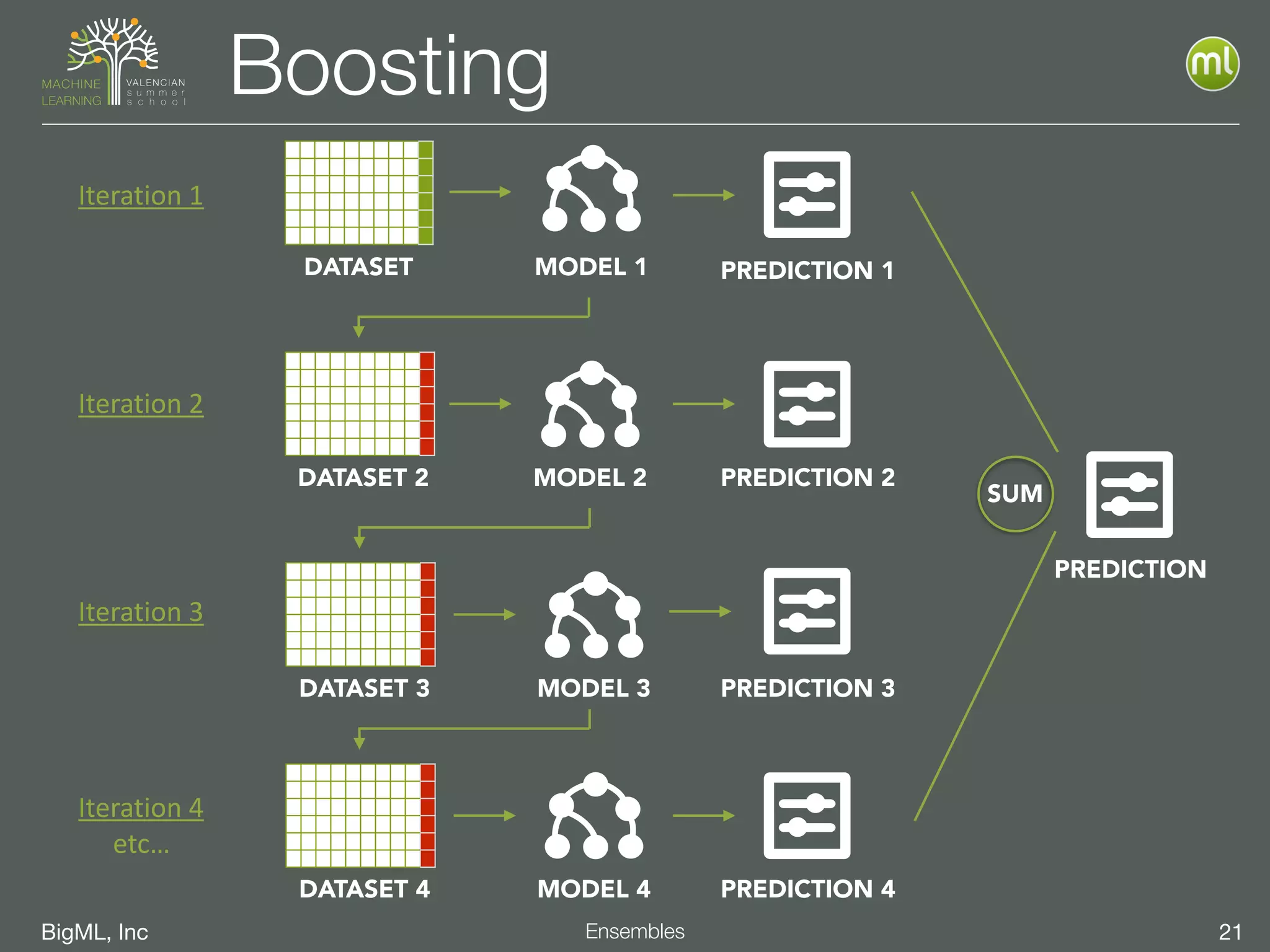
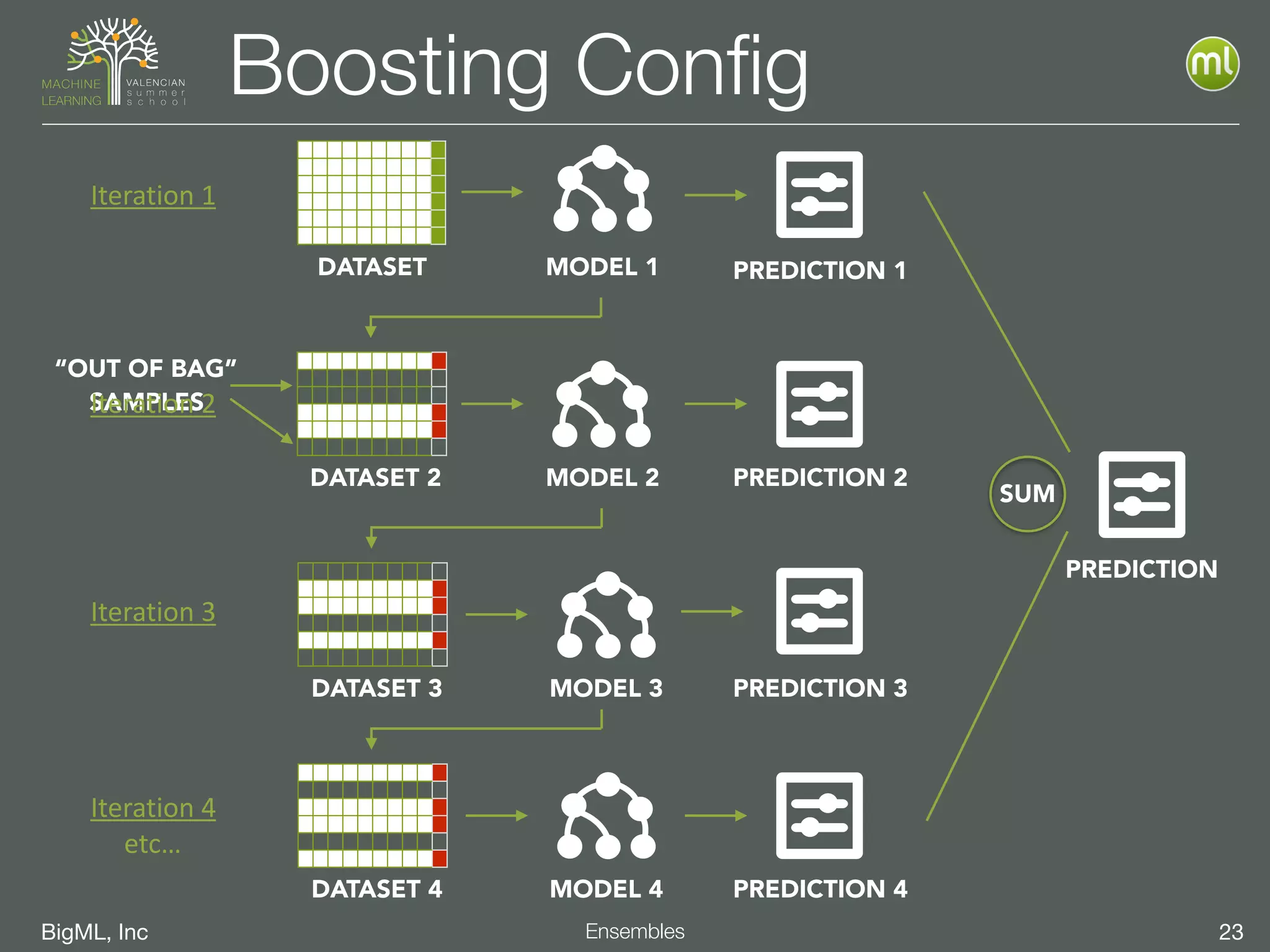
The document discusses the concept of ensemble methods in machine learning, highlighting their importance in combining multiple weaker models to create a more powerful predictive model. It addresses the inherent imperfections of both models and data, emphasizing techniques like bootstrapping, random decision forests, and boosting for better performance. The document also covers different ensemble strategies and offers guidelines on selecting appropriate methods based on data characteristics and challenges.


































![BigML, Inc 14Logistic Regressions
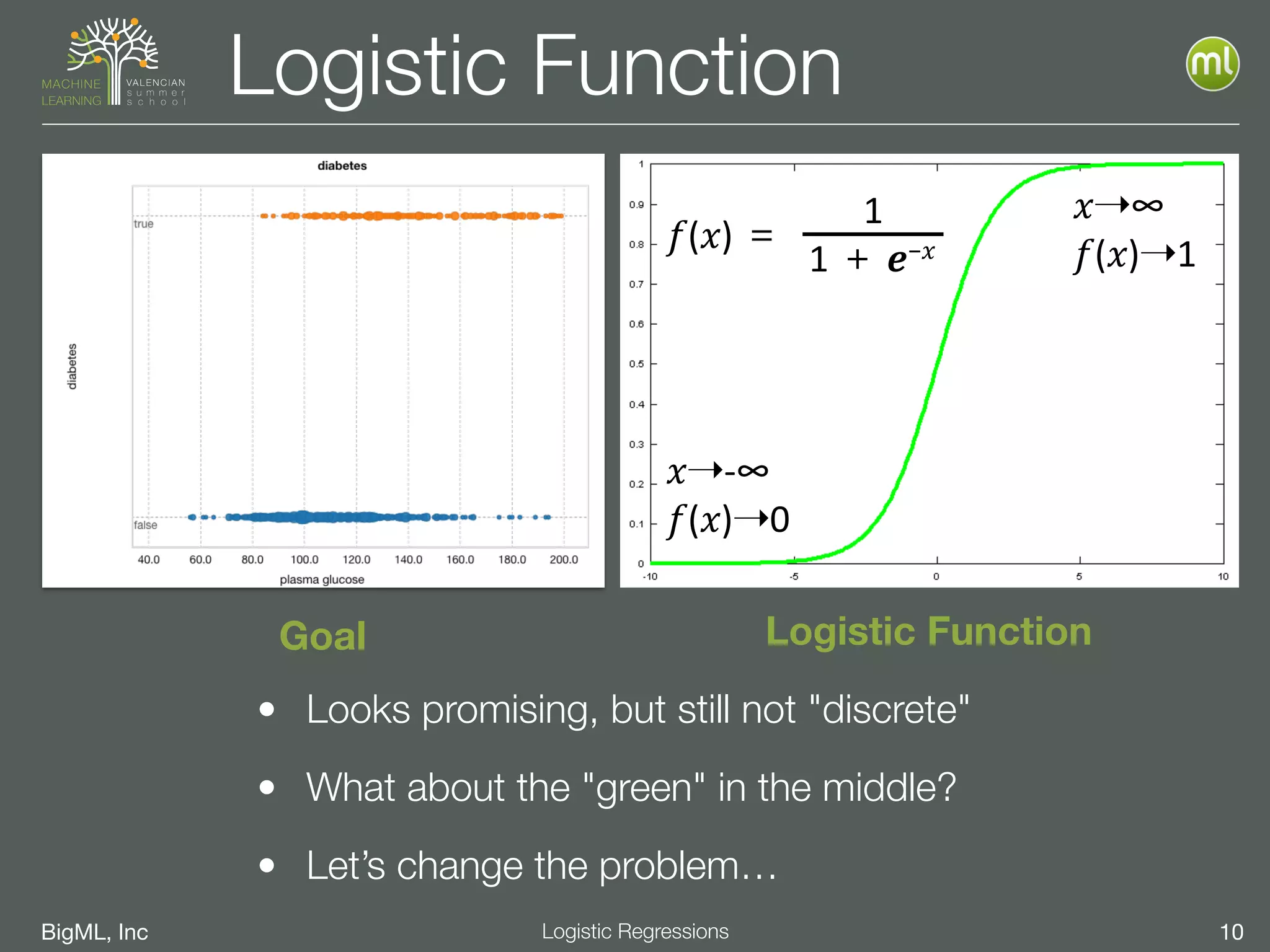
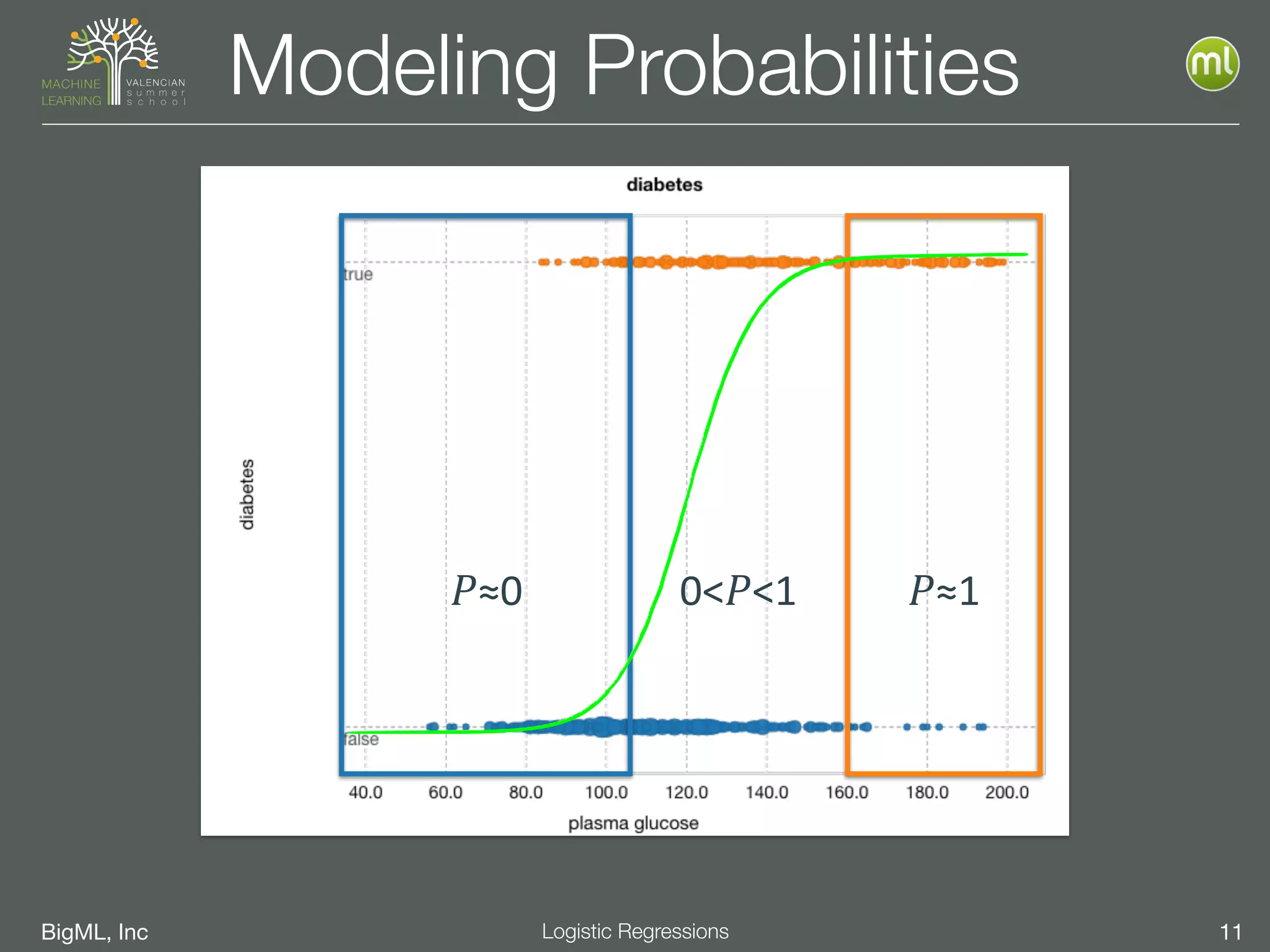
Logistic Regression
For "𝑖" dimensions, 𝑿﹦[
𝑥1,
𝑥2,⋯,
𝑥𝑖
],
we solve
𝑃(𝑿)=
1
1+𝑒−𝑓(𝑿)
𝑓(𝑿)=𝛽0+𝞫·∙𝑿=𝛽0+𝛽1 𝑥1+⋯+𝛽𝑖 𝑥𝑖
where:](https://image.slidesharecdn.com/vssml17-l2-ensembles-logisticregressions-170918170823/75/VSSML17-L2-Ensembles-and-Logistic-Regressions-52-2048.jpg)
![BigML, Inc 15Logistic Regressions
Interpreting Coefficients
• LR computes 𝛽0 and coefficients 𝛽𝑗 for each feature 𝑥𝑗
• negative 𝛽𝑗 → negatively correlated:
• positive 𝛽𝑗 → positively correlated:
• "larger" 𝛽𝑗 → more impact:
• "smaller" → less impact:
• 𝛽𝑗
"size" should not be confused with field importance
• Can include a coefficient for "missing" (if enabled)
• 𝑃(𝑿)
=
𝛽0+⋯+𝛽𝑗 𝑥𝑗+⋯
• Binary Classification (true/false) coefficients are complementary
• 𝑃(True)
≡
1−
𝑃(False)
+𝛽𝑗+1[
𝑥𝑗
≡
Missing
]
𝑥𝑗↑
then
𝑃(𝑿)↓
𝑥𝑗↑
then
𝑃(𝑿)↑
𝑥𝑗≫
then
𝑃(𝑿)﹥
𝑥𝑗﹥then
𝑃(𝑿)≫](https://image.slidesharecdn.com/vssml17-l2-ensembles-logisticregressions-170918170823/75/VSSML17-L2-Ensembles-and-Logistic-Regressions-53-2048.jpg)



![BigML, Inc 19Logistic Regressions
LR - Multi Class
• Instead of a binary class ex: [ true, false ],
we have multi-class ex: [ red, green, blue, … ]
• "𝑘" classes: 𝑪=[𝑐1,
𝑐2,⋯,
𝑐 𝑘]
• solve one-vs-rest LR
• Result: 𝞫𝑗 for each class 𝑐𝑗
• apply combiner to ensure
all probabilities add to 1
𝑙𝑛( )𝑃(𝑐1)
𝑃(𝑐1ʹ′)
=𝛽1,0+𝞫1·∙𝑿
𝑙𝑛( )𝑃(𝑐2)
𝑃(𝑐2ʹ′)
=𝛽2,0+𝞫2·∙𝑿
⋯
𝑙𝑛( )𝑃(𝑐 𝑘)
𝑃(𝑐 𝑘ʹ′)
=𝛽 𝑘,0+𝞫 𝑘·∙𝑿](https://image.slidesharecdn.com/vssml17-l2-ensembles-logisticregressions-170918170823/75/VSSML17-L2-Ensembles-and-Logistic-Regressions-57-2048.jpg)